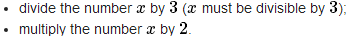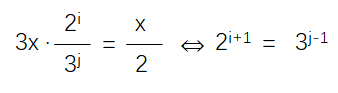Codeforces Round #479 (Div. 3) D. Divide by three, multiply by two
D. Divide by three, multiply by two
•题意
给你一个数 x,x 可以执行以下两种操作中的一种得到数 y:
y 再执行上述两种操作的一种得到数 z;
接着对 z 得到......
这样依次执行了 n-1 次会得到 n 个数;
现在给你这 n 个数,让你按照上述规则给这 n 个数排序,使得其满足
a1=x , a2=y , a3=z , ........
输出这 n 个数;
•题解
对于任意一个数 x,能通过两种操作得到:
①3x除以3
②x/2乘2
你会发现,3x 与 x/2 不会同时出现,因为如果同时出现,为什么呢?
假设 3x 经过 i 次乘2操作,j次除以3的操作得到 x/2,即
因为GCD(2,3) = 1,所以右边的等式是不可能成立的;
所以 x 只能由①②中的一种情况得到;
并且这 n 个数各不相同;
那么,任意选取一个数,依次向前推,依次向后推即可得到答案;
•Code
 View Code1 #include<bits/stdc++.h> 2 using namespace std; 3 #define ll long long 4 const int maxn=100+50; 5 6 int n; 7 ll a[maxn]; 8 map<ll ,bool>f; 9 10 void Solve() 11 { 12 ll x=a[1]; 13 while(true)///找到x 14 { 15 if(f.count(x*3)) 16 x *= 3; 17 else if(!(x&1) && f.count(x/2)) 18 x /= 2; 19 else 20 break; 21 } 22 printf("%lld",x);///由x开始依次向后推 23 for(int i=2;i <= n;++i) 24 { 25 if(f.count(x*2)) 26 x *= 2; 27 else 28 x /= 3; 29 printf(" %lld",x); 30 } 31 printf("\n"); 32 } 33 int main() 34 { 35 scanf("%d",&n); 36 for(int i=1;i <= n;++i) 37 { 38 scanf("%lld",a+i); 39 f[a[i]]=true; 40 } 41 Solve(); 42 43 return 0; 44 }
View Code1 #include<bits/stdc++.h> 2 using namespace std; 3 #define ll long long 4 const int maxn=100+50; 5 6 int n; 7 ll a[maxn]; 8 map<ll ,bool>f; 9 10 void Solve() 11 { 12 ll x=a[1]; 13 while(true)///找到x 14 { 15 if(f.count(x*3)) 16 x *= 3; 17 else if(!(x&1) && f.count(x/2)) 18 x /= 2; 19 else 20 break; 21 } 22 printf("%lld",x);///由x开始依次向后推 23 for(int i=2;i <= n;++i) 24 { 25 if(f.count(x*2)) 26 x *= 2; 27 else 28 x /= 3; 29 printf(" %lld",x); 30 } 31 printf("\n"); 32 } 33 int main() 34 { 35 scanf("%d",&n); 36 for(int i=1;i <= n;++i) 37 { 38 scanf("%lld",a+i); 39 f[a[i]]=true; 40 } 41 Solve(); 42 43 return 0; 44 }