Codeforces Round #564 (Div. 2) D. Nauuo and Circle（树形DP）

D. Nauuo and Circle

•参考资料

　　[1]:https://www.cnblogs.com/wyxdrqc/p/10990378.html

•题意

　　给出你一个包含 n 个点的树，这 n 个点编号为 1~n；

　　给出一个圆，圆上放置 n 个位置，第 i 个位置对应树中的某个节点，并且不重复；

　　求在圆上还原这棵树后，使得边不相交的总方案数；

•题解

　　

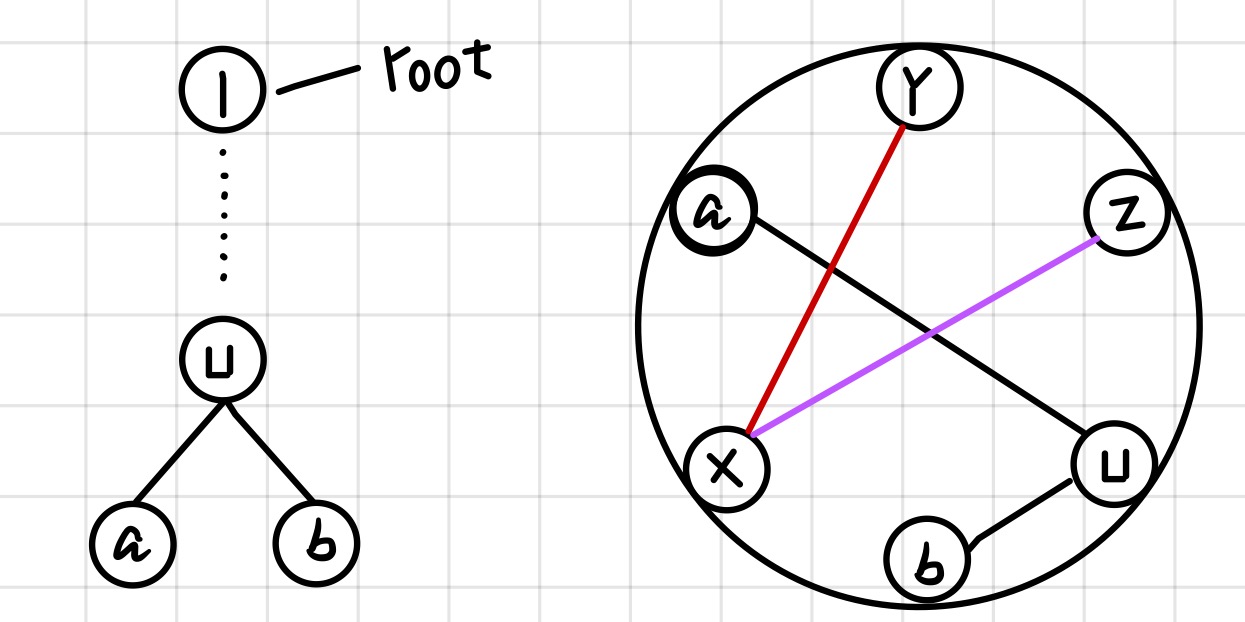
　　①为何每一颗子树一定是连续的一段圆弧？

　　　　假设不是连续的圆弧，如图所示：

　　　　

　　　　为了使 x 接到树上，必然会有 x-y 或 x-z 相连的边，这样就会出现交点；

　　②对于以 u 为根的子树，假设 u 有两个儿子 a,b，那么，需要找连续的 x+y+1 个位置放置这些节点；

　　　　

　　　　（x:以a为根节点的子树节点个数，y:以b为根节点的子数的节点个数）

　　　　也就是图中的sum1,sum2,sum3位置；

　　　　u可以放在这三个位置的任意一个位置，a 从剩余的两个位置中选，b只有一个位置可选；

　　　　总的方案数为 3!；

　　　　但是每个方案中 a,b 都有排列方案，故需要乘上 fa×fb；

 　　　　对于树的根节点 1，一共有 n 个位置可放，求出其中一个的方案数 f1，答案就是 n×f1；

•Code

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 #define ll long long
 4 #define memF(a,b,n) for(int i=0;i <= n;a[i++]=b);
 5 const int maxn=2e5+50;
 6 const int MOD=998244353;
 7 
 8 int n;
 9 int num;
10 int head[maxn];
11 struct Edge
12 {
13     int to,next;
14 }G[maxn<<1];
15 void addEdge(int u,int v)
16 {
17     G[num]=Edge{v,head[u]};
18     head[u]=num++;
19 }
20 ll fact[maxn];
21 ll dp[maxn];///与f函数功能相同
22 vector<int >son[maxn];
23 void DFS(int u,int f)
24 {
25     for(int i=head[u];~i;i=G[i].next)
26     {
27         int v=G[i].to;
28         if(v == f)
29             continue;
30 
31         son[u].push_back(v);
32         DFS(v,u);
33     }
34     
35     int k=son[u].size()+(u != 1 ? 1:0);///如果u=1就不用再找u可放置的位置，因为1已经被固定了
36     dp[u]=fact[k];
37     for(int i=0;i < son[u].size();++i)
38         dp[u]=dp[u]*dp[son[u][i]]%MOD;
39 }
40 ll Solve()
41 {
42     for(int i=0;i <= n;++i)
43         son[i].clear();
44 
45     DFS(1,1);
46 
47     return dp[1]*n%MOD;
48 }
49 void Init()
50 {
51     num=0;
52     memF(head,-1,n);
53     fact[0]=1;
54     for(int i=1;i <= n;++i)
55         fact[i]=(i*fact[i-1])%MOD;
56 }
57 int main()
58 {
59     scanf("%d",&n);
60     Init();
61     for(int i=1;i < n;++i)
62     {
63         int u,v;
64         scanf("%d%d",&u,&v);
65         addEdge(u,v);
66         addEdge(v,u);
67     }
68     printf("%lld\n",Solve());
69     return 0;
70 }
View Code
posted @ 2019-06-08 18:42  HHHyacinth  阅读(559)  评论(0)  编辑  收藏  举报