UPC 2019年第二阶段我要变强个人训练赛第六场

1 题目描述 2 小D从家到学校的道路结构是这样的:由n条东西走向和m条南北走向的道路构成了一个n*m的网格,每条道路都是单向通行的(只能从北向南,从西向东走)。 3 已知小D的家在网格的左上角,学校在网格的右下角。 4 问小D从他的家到学校一共有多少种不同的上学路线。 5 (配图如下) 6 输入 7 两个正整数n和m,意义如题目所述。 8 9 输出 10 小D上学路线数量,结果对1000000007取余。
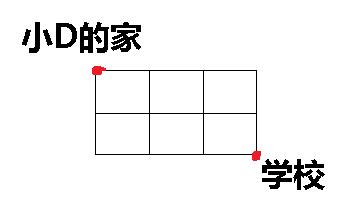

1 样例输入 2 3 4 3 样例输出 4 10
思路一(递推):
1 ll dp[maxn][maxn];///dp[i][j]:从点(i,j)到(n,m)的路线个数
初始化dp[n][m]=1;
AC代码:

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=1e3+50; 4 #define ll long long 5 #define mem(a,b) memset(a,b,sizeof(a)) 6 const int MOD=1000000007; 7 8 int n,m; 9 ll dp[maxn][maxn]; 10 11 ll Solve() 12 { 13 mem(dp,0); 14 for(int i=n;i >= 1;--i) 15 { 16 for(int j=m;j >= 1;--j) 17 { 18 if(i == n && j == m) 19 dp[i][j]=1; 20 else 21 dp[i][j]=(dp[i+1][j]+dp[i][j+1])%MOD; 22 } 23 } 24 return dp[1][1]%MOD; 25 } 26 int main() 27 { 28 scanf("%d%d",&n,&m); 29 printf("%lld\n",Solve()); 30 31 return 0; 32 }
思路二(记忆化搜索 by mxl):
由题意可知,一共向下走了 n-1 步;
那么对于第 i 列可能向下走连续的 0,1,2,...,n-1 步;
ll dp[maxn][maxn];///dp[i][j]:第i列向下走连续的j步含有的总方案数
初始化dp为-1;
AC代码:

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=1e3+50; 4 #define ll long long 5 #define mem(a,b) memset(a,b,sizeof(a)) 6 const int MOD=1000000007; 7 8 int n,m; 9 ll dp[maxn][maxn];///dp[i][j]:第i列向下走连续的j步含有的总方案数 10 11 ll DFS(int cur,int cnt)///第cur列最多向下走cnt步 12 { 13 if(cur > m) 14 return cnt == 0 ? 1:0; 15 16 if(dp[cur][cnt] != -1)///记忆化搜索 17 return dp[cur][cnt]; 18 19 ll ans=0; 20 for(int i=0;i <= cnt;++i)///第cur列向下走i步 21 ans=(ans+DFS(cur+1,cnt-i))%MOD; 22 23 dp[cur][cnt]=ans; 24 return ans; 25 } 26 ll Solve() 27 { 28 mem(dp,-1); 29 return DFS(1,n-1)%MOD; 30 } 31 int main() 32 { 33 scanf("%d%d",&n,&m); 34 printf("%lld\n",Solve()); 35 36 return 0; 37 }




