hdu 3530 "Subsequence" (单调队列)
题意:
给出一个序列,求最长的连续子序列,使得 m ≤ Max-Min ≤ k
我的理解:
定义数组 a[] 存储输入的 n 个数;
定义两个双端队列:
deque<int >qMax,qMin;
qMax : 维护前 i 个数的最大值(非递增序列);
qMin : 维护前 i 个数的最小值(非递增序列);
1 for(int i=1;i <= n;++i) 2 { 3 ///注意此处用了'=',也就是说,队列中的所有数都互异 4 while(!qMax.empty() && a[qMax.back()] <= a[i]) 5 qMax.pop_back();///保证qMax递减 6 qMax.push_back(i); 7 while(!qMin.empty() && a[qMin.back()] >= a[i]) 8 qMin.pop_back();///保证qMin递增 9 qMin.push_back(i); 10 }
例如:
1 2 3 4 5 6
val: 9 6 5 1 2 3
i = 6 时的队列情况(此处队列中维护的是值,便于理解):
qMax : {9,6,5,3};
qMin : {1,2,3};
假设来到 i 位置(队列维护下标):
qMax : { φ1,φ2,φ3,...,i };(下标递增,下标对应的值递减)
qMin : { ω1,ω2,ω3,....,i }:(下标递增,下标对应的值递增)
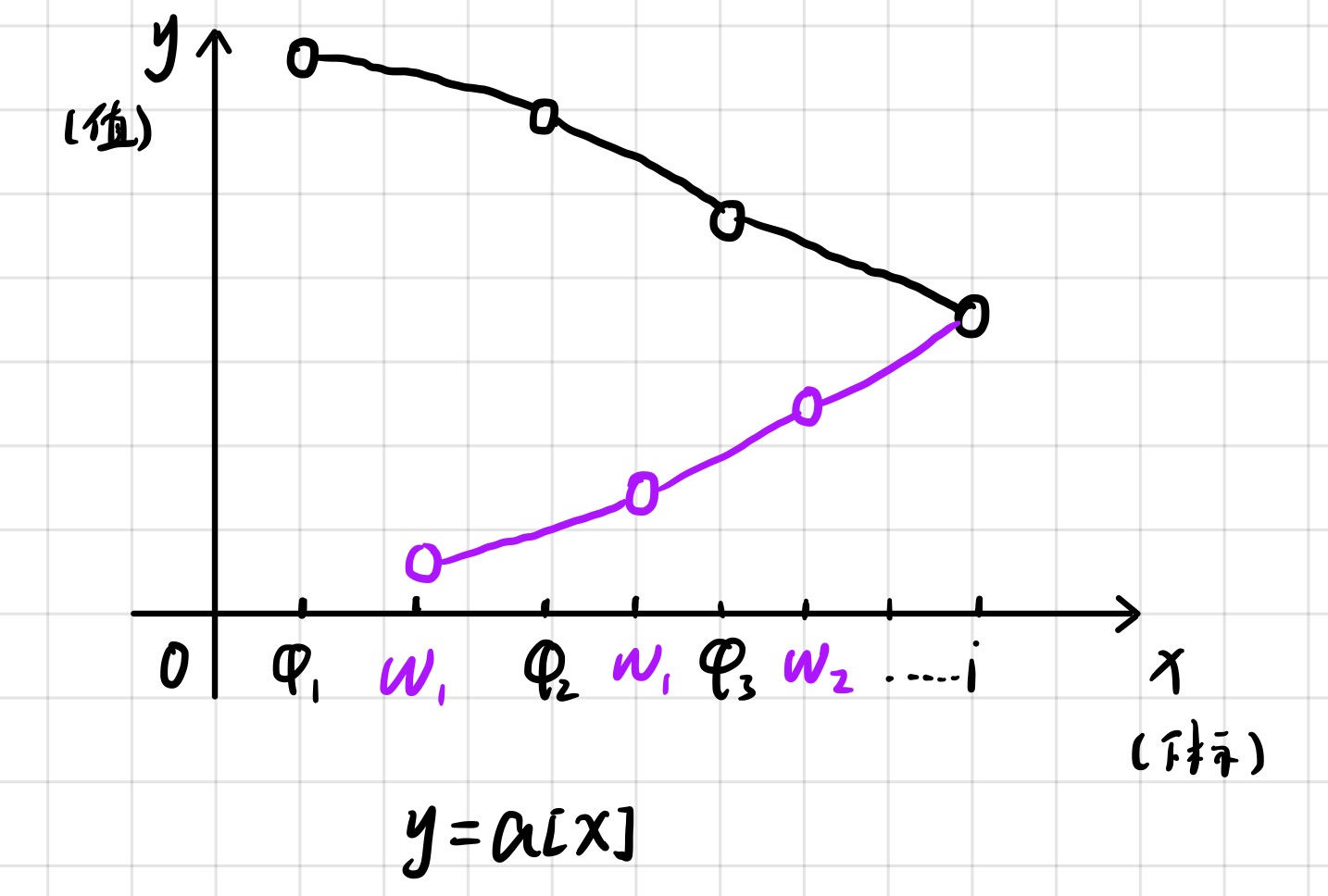
(φ1,φ2,φ3,...ω1,ω2,ω3 互不相同,当然 i 除外)
(qMax.val ≥ qMin.val,下标对应的值)
下面看看队列的操作(pos初始为1):
1 while(a[qMax.front()]-a[qMin.front()] > k) 2 { 3 if(qMax.front() < qMin.front()) 4 { 5 pos=qMax.front()+1; 6 qMax.pop_front(); 7 } 8 else 9 { 10 pos=qMin.front()+1; 11 qMin.pop_front(); 12 } 13 } 14 if(a[qMax.front()]-a[qMin.front()] >= m) 15 ans=max(ans,i-pos+1);
首先判断 qMax.front() 对应的值(假设为 a[φ1]) 与 qMin.front() 对应的值(假设为 a[ω1])做差是否大于 k;
如果大于,那么,如何使差值变小呢?
操作①qMax.pop_front(),(φ1 -> φ2)下一位对应的值更小
操作②qMin.pop_front(),(ω1 -> ω2)下一位对应的值更大
操作①②都可以使他们两者的差值变小,那么,到底该用哪个操作呢?
答案:谁的下标小,弹出谁,并且,所有的出队操作是不可能使队列为空的,因为两个队列中都有a[ i ]这个元素;
为什么要这么做呢?
假设不这么做,那么就是谁的下标大,弹出谁,假设 φ1 > ω1 ;
那么,就需要弹出φ1 ,那么,包含当前最值的区间为[ ω1 ,φ2],但是,φ1 也在其中,最大值就不该是a[φ1 ]而应该是a[φ2];
所以,谁的下标小,弹出谁;
pos作用又是啥呢?
找到包含 a[ i ] 的,并且满足条件的最大的区间,也就是[pos,i]是包含a[i]的最大的区间;
那,为什么pos=front()+1就一定对呢?
假设当前弹出的是φ1 ,也就是说a[φ1]-a[ω1] > t,假设 a[φ2]-a[ω1] ≤ t;
那么,a[pos]-a[ω1] ≤ t;
因为a[pos] ≤ a[φ2],在 φ2 满足条件的情况下,pos一定满足条件,且是满足条件的最大的区间(φ1不满足);
为什么不用判断其是否 ≥ m 呢?
因为操作①②都是使差值减小,只有可能在后面的更新队列的操作中使其差值增大;
AC代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<deque> 4 using namespace std; 5 const int maxn=1e5+50; 6 7 int n,m,k; 8 int a[maxn]; 9 deque<int >qMax,qMin; 10 11 int Solve() 12 { 13 qMax.clear(); 14 qMin.clear(); 15 16 int ans=0; 17 int pos=1; 18 for(int i=1;i <= n;++i) 19 { 20 ///注意此处用了'=',也就是说,队列中的所有数都互异 21 ///不加'='也行,不影响答案,因为在弹出操作时,qMax,qMin都将等于a[i]的给去了 22 ///那么,a[i]本身是不会更新pos的值 23 ///就算是队列末尾有重复的a[i]也不会更新pos,这就保证了pos的正确性 24 ///[pos,i]是包含a[i]的最大的区间 25 while(!qMax.empty() && a[qMax.back()] <= a[i]) 26 qMax.pop_back(); 27 qMax.push_back(i); 28 while(!qMin.empty() && a[qMin.back()] >= a[i]) 29 qMin.pop_back(); 30 qMin.push_back(i); 31 32 while(a[qMax.front()]-a[qMin.front()] > k)///最坏的情况是最后两个队列只剩下a[i] 33 { 34 if(qMax.front() < qMin.front()) 35 { 36 pos=qMax.front()+1; 37 qMax.pop_front(); 38 } 39 else 40 { 41 pos=qMin.front()+1; 42 qMin.pop_front(); 43 } 44 } 45 if(a[qMax.front()]-a[qMin.front()] >= m) 46 ans=max(ans,i-pos+1);///判断[pos,i]区间是否更新ans 47 } 48 return ans; 49 } 50 int main() 51 { 52 while(~scanf("%d%d%d",&n,&m,&k)) 53 { 54 for(int i=1;i <= n;++i) 55 scanf("%d",a+i); 56 printf("%d\n",Solve()); 57 } 58 return 0; 59 }




