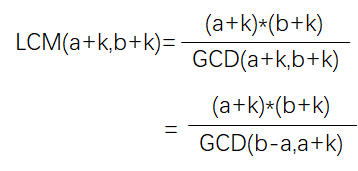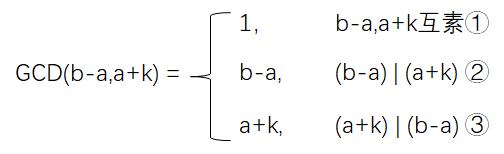Codeforces Round #554 (Div. 2) C. Neko does Maths（GCD(a,b) = GCD(a,b-a)）

传送门

 

•题意

　　给出两个正整数 a,b；

　　求解 k ，使得 LCM(a+k,b+k) 最小，如果有多个 k 使得 LCM() 最小，输出最小的k；

•思路

　　刚开始推了好半天公式，一顿xjb乱操作；

　　后来，看了一下题解，看到一个引理：

　　GCD(a,b) = GCD(a,b-a) = GCD(b,b-a);

假设GCD(a,b) = c;
a%c = 0;
b%c = 0;
那么(b-a)%c = 0;
这证明了a和(b-a),b和(b-a)有公约数c;
假设GCD(a,b-a)=c' > c;
那么，a%c' = 0;
(b-a)%c' = 0;
(b-a)%c' = b%c'-a%c';
所以 b%c' = 0;
那么GCD(a,b) = c' > c，与假设矛盾；
GCD(b,b-a)同理；
故命题得证；
简单证明

　　有了这个引理后，解题思路变得异常清晰；

　　首先，令 b > a；

　　将 LCM(a+k,b+k) 转化一下：

　　

　　

　　情况①，如果 a 与 b-a 不互素，那么 a+1 与 b-a 一定互素；

　　情况②，a+k = x·(b-a)，其中 x·(b-a) 是大于等于 a 的最小的 (b-a) 的倍数；

　　情况③，枚举 b-a 的约数；

•Code

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 using namespace std;
 5 #define ll long long
 6 
 7 ll a,b;
 8 
 9 ll GCD(ll a,ll b)
10 {
11     return a == 0 ? b:GCD(b%a,a);
12 }
13 ll LCM(ll a,ll b)
14 {
15     return a/GCD(a,b)*b;
16 }
17 ll F(ll k)
18 {
19     return (a+k)*(b+k)/GCD(a+k,b+k);
20 }
21 bool isSat(int i,ll k)//判断k是否可以更新为i-a
22 {
23     ll curK=i-a;
24     if(curK < 0 || F(curK) != LCM(a+curK,b+curK))
25         return false;
26     if(F(curK) < F(k) || F(curK) == F(k) && curK < k)
27         return true;
28     return false;
29 }
30 ll Solve()
31 {
32     if(a > b)
33         swap(a,b);
34     int d=b-a;
35     if(d == 0)
36         return 0;
37 
38     ll k=1;
39     for(;GCD(d,a+k) != 1;k++);///情况①
40     for(int i=1;i*i <= d;++i)///情况③
41     {
42         if(d%i != 0)
43             continue;
44         if(isSat(i,k))///a+k=i
45             k=i-a;
46         if(isSat(d/i,k))///a+k=d/i
47             k=d/i-a;
48     }
49     ///情况②，GCD()为定值，k越小LCM()就越小
50     ll x=(a/d+(a%d == 0 ? 0:1))*d;///a+k=k*d(k*d:>=a的最小的d的倍数)
51     if(isSat(x,k))
52         k=x-a;
53 
54     return k;
55 }
56 int main()
57 {
58     scanf("%lld%lld",&a,&b);
59     printf("%lld\n",Solve());
60 
61     return 0;
62 }
View Code

 

分割线：2019.7.23

•新想法

　　GCD(b-a , a+k) = f(b-a);

　　f(b-a) 表示 b-a 的约数；

　　当 GCD(b-a,a+k) 确定后，k 越小则 LCM(a+k,b+k) 就越小；

　　假设 GCD(b-a,a+k) = f;

　　①如果 a 本身就为 f 的倍数，且 GCD(b-a,a) = f;

　　那么 k = 0 是满足当前条件下，使得 LCM(a+k,b+k) 最小的最优解；

　　②反之，如果 a 不为  f 的倍数，那么，找到 ≥ a 的最小的 x·f，并判断 GCD(b-a,x·f) ?= f；

　　　　1)如果 GCD(b-a,x·f) = f;

　　　　　　那么 k = x·f-a 是满足当前条件下，使得 LCM(a+k,b+k) 最小的最优解；

　　　　2)如果 GCD(b-a,x·f) ≠ f;

　　　　　　那么 GCD(b-a,(x+1)·f)一定等于 f；

　　GCD(b-a,x·f) = GCD(y·f,x·f) = f·GCD(x,y);

　　判断 GCD(b-a,x·f) ?= f ⇔ 判断 GCD(y,x) ?= 1;

　　如果 GCD(y,x) ≠ 1，那么一定有 GCD(y,x+1) = 1;

•Code

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 #define GCD(a,b) __gcd(a,b)
 4 #define ll long long
 5 
 6 ll a,b;
 7 
 8 ll g(ll k)
 9 {
10     return (a+k)/GCD(a+k,b+k)*(b+k);
11 }
12 void update(ll f,ll &k)
13 {
14     ll x=a/f+(a%f != 0);///找到使得x·f ≥ a的最小的x
15     ll y=(b-a)/f;
16 
17     if(GCD(x,y) != 1)
18         x++;
19 
20     ///判断是否更新k
21     ll cur=x*f-a;
22     if(k == -1 || g(k) > g(cur))
23         k=cur;
24     else if(g(k) == g(cur))
25         k=min(k,cur);
26 }
27 ll Solve()
28 {
29     if(a == b)
30         return 0;
31     if(b < a)
32         swap(a,b);
33 
34     ll k=-1;
35 
36     for(ll i=1;i*i <= b-a;++i)
37     {
38         if((b-a)%i != 0)
39             continue;
40 
41         update(i,k);
42         update((b-a)/i,k);
43     }
44 
45     return k;
46 }
47 int main()
48 {
49     scanf("%lld%lld",&a,&b);
50     printf("%lld\n",Solve());
51 
52     return 0;
53 }
View Code

 

　　　　　　

 

posted @ 2019-04-25 20:18  HHHyacinth  阅读(793)  评论(0)  编辑  收藏  举报