Stanford Local 2016 E "Election of Evil"(搜索(正解)或并查集(划掉))
题意:
给出集合U,V,集合U有n个元素,集合V有m个元素;
有 m 个操作,mi : s1 s2 有一条s1指向s2的边(s1,s2可能属于第三个集合,暂且称之为K集合);
指向边具有传递性,即 A->B,B->C <=> A->C
求V集合中被 U 指向的元素;
题解:
并查集debug个了两天,始终wa,今天上午上数字逻辑课的时候,灵光一闪,又想到了一个可能会出错的点;
经过一番挣扎,终于判断了此题不能用并查集做,蓝瘦香菇~~~~~~
还记得并查集中的Union(x,y)操作吗?
此函数得作用是将 x元素 所在的集合与 y元素 所在得集合合并成一个大集合;
对于此题,初始想法是,并查集中只保存
①U 集合指出去的边
②K 集合指向 V 集合的边
③V 集合指向 V 集合的边
如果满足上述三种条件,则Union(s1,s2);
最后,判断V集合中元素的Find(s)是否属于U集合,如果属于,则输出s;
那么,问题来了,s1,s2真的可以这么合并吗?
看如下连接方式:
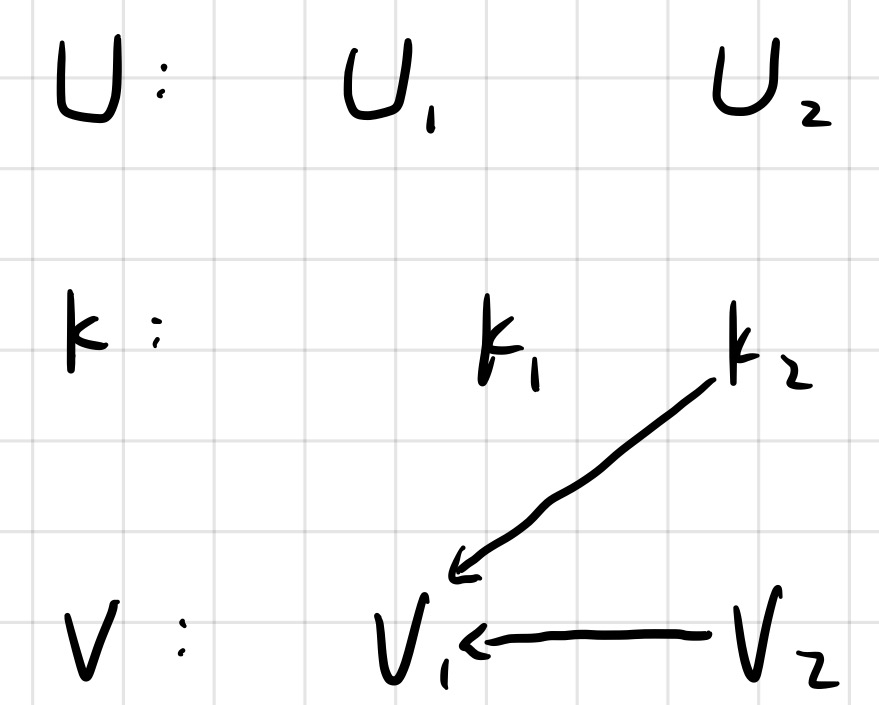
输入的顺序是:
v2 v1
k2 v1
对于第一条指令,Union(v2,v1)是没得说的,此时 fa(v1) = v2 , fa(v2) =v2;
对于第二条指令,可以调用 Union(k2,v1) 吗?
先看看调用后的结果:Find(k2) = k2 , Find(v1) = v2 , k2 ≠ v2 , fa(v1)=fa(v2)=k2; ???
那么,再加入一条边呢?
u1 k2
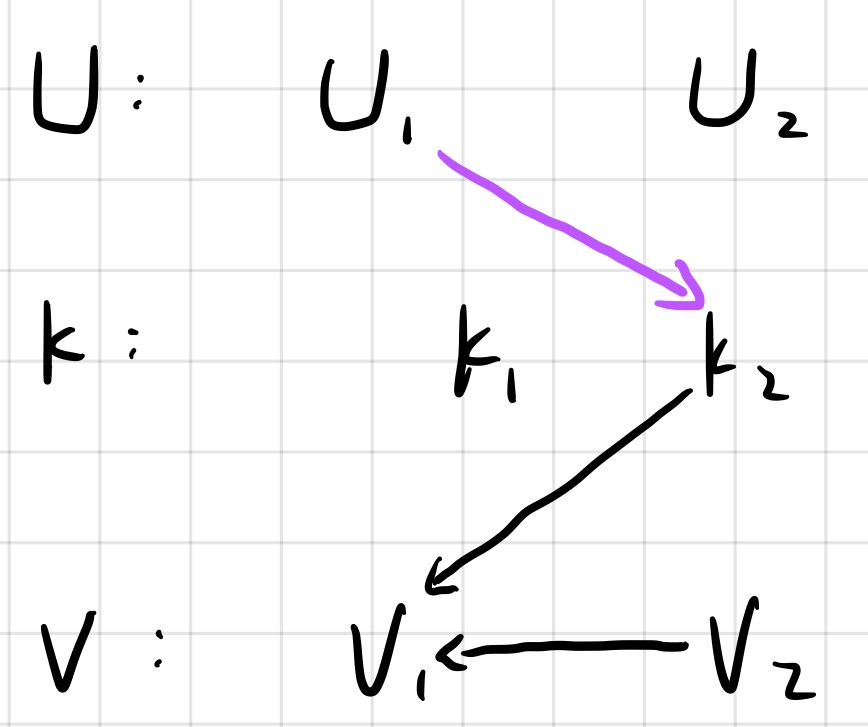
那么,此时调用Union(u1,k2) : fa(k2) = u1;
当输出时:
v1 : Find(v1) = Find(k2) = u1 ,输出 v1
v2 : Find(v2) = Find(k2) = u1 ,输出 v2
这就出现问题了吧!!!
那,如果人为的将 fa(v1) = k2,但是fa(v2) = v2呢?
看一下接下来的这张图:
加入边 u2 v2
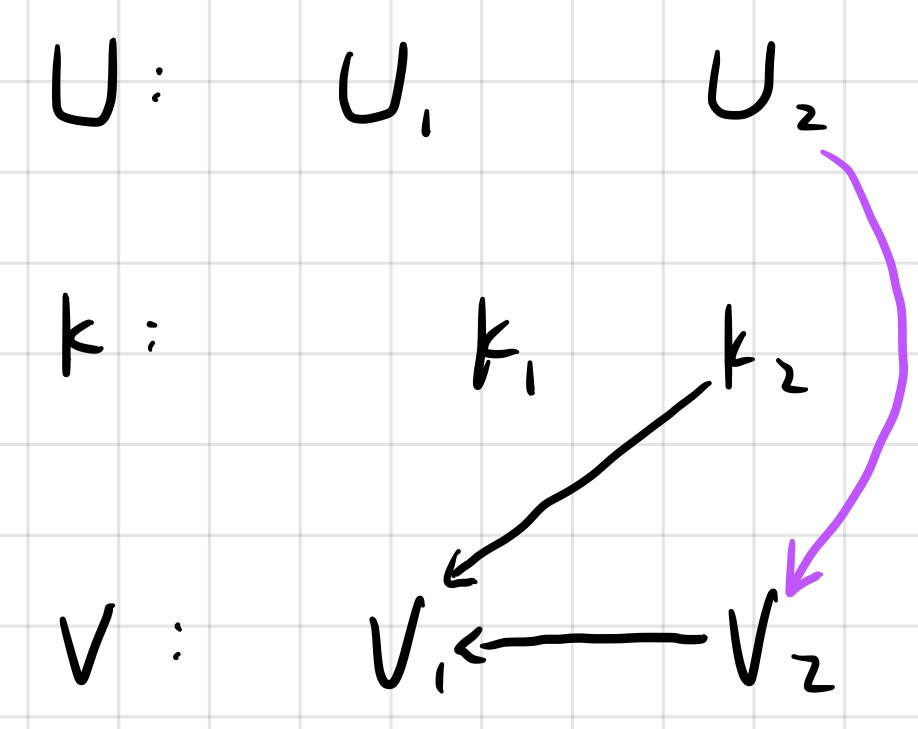
输出时:
v1 : Find(v1) = k2 ,不输出 v1
v2 : Find(v2) = u2 ,输出 v2
又出现错误了,是吧!
为什么并查集会出现这个问题呢?
v1,v2属于同一个集合,v1,k2属于同一个集合,但 k2,v2并不能属于同一个集合,所以不能合并;
看来,当图是有向图时,慎用并查集!!!!!!!!!!!!!
所以说,还是搜索大法好!!!!
AC代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<map> 4 #include<cstring> 5 using namespace std; 6 #define mem(a,b) memset(a,b,sizeof(a)) 7 const int maxn=1e4+50; 8 9 int n,m,x; 10 int numU,numV;//[1,numU]集合U的编号范围,[numU+1,numV]:集合V的编号范围 11 bool vis[maxn];//vis[i]:判断属于V集合的编号i是否有条被U集合指向的边 12 bool rep[maxn];//rep[i]:判断i编号对应的字符串是否重复出现在U,V集合中 13 int head[maxn]; 14 int num; 15 struct Edge 16 { 17 int to; 18 int next; 19 }G[2*maxn]; 20 void addEdge(int u,int v) 21 { 22 G[num].to=v; 23 G[num].next=head[u]; 24 head[u]=num++; 25 } 26 map<string ,int >mymap;//将字符串映射成整数 27 28 bool isSetU(int xx)//判断节点xx是否属于U集合 29 { 30 return xx >= 1 && xx <= numU; 31 } 32 bool isSetV(int xx)//判断节点xx是否属于V集合 33 { 34 return xx > numU && xx <= numV; 35 } 36 void DFS(int u) 37 { 38 vis[u]=true;//被集合U指向的节点 39 for(int i=head[u];~i;i=G[i].next) 40 { 41 int v=G[i].to; 42 if(!vis[v]) 43 DFS(v); 44 } 45 } 46 void Solve(int id) 47 { 48 for(int i=1;i <= x;++i) 49 { 50 string s1,s2; 51 cin>>s1>>s2; 52 if(!mymap.count(s1)) 53 mymap[s1]=++id; 54 if(!mymap.count(s2)) 55 mymap[s2]=++id; 56 int u=mymap[s1]; 57 int v=mymap[s2]; 58 addEdge(u,v); 59 } 60 map<string ,int>::iterator it; 61 for(it=mymap.begin();it != mymap.end();++it) 62 { 63 int x=it->second; 64 if(!isSetU(x) || vis[x]) 65 continue; 66 //以集合U中的元素为起点开始搜索 67 DFS(x); 68 } 69 bool flag=false; 70 for(it=mymap.begin();it != mymap.end();++it) 71 { 72 int x=it->second; 73 if(rep[x] || isSetV(x)&&vis[x]) 74 { 75 if(!flag) 76 cout<<it->first; 77 else 78 cout<<" "<<it->first; 79 flag=true; 80 } 81 } 82 cout<<"\n"; 83 } 84 void Init() 85 { 86 num=0; 87 mem(head,-1); 88 mem(rep,false); 89 mem(vis,false); 90 mymap.clear(); 91 } 92 int main() 93 { 94 // freopen("C:\\Users\\hyacinthLJP\\Desktop\\in&&out\\contest","r",stdin); 95 ios::sync_with_stdio(false); 96 cin.tie(0); 97 cout.tie(0); 98 99 int test; 100 cin>>test; 101 while(test--) 102 { 103 Init(); 104 cin>>n>>m>>x; 105 int id=0; 106 for(int i=1;i <= n;++i) 107 { 108 string s; 109 cin>>s; 110 mymap[s]=++id; 111 } 112 numU=id; 113 for(int i=1;i <= m;++i) 114 { 115 string s; 116 cin>>s; 117 if(!mymap.count(s)) 118 mymap[s]=++id; 119 else 120 rep[mymap[s]]=true;//重复出现的字符串 121 } 122 numV=id; 123 Solve(id); 124 } 125 return 0; 126 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号