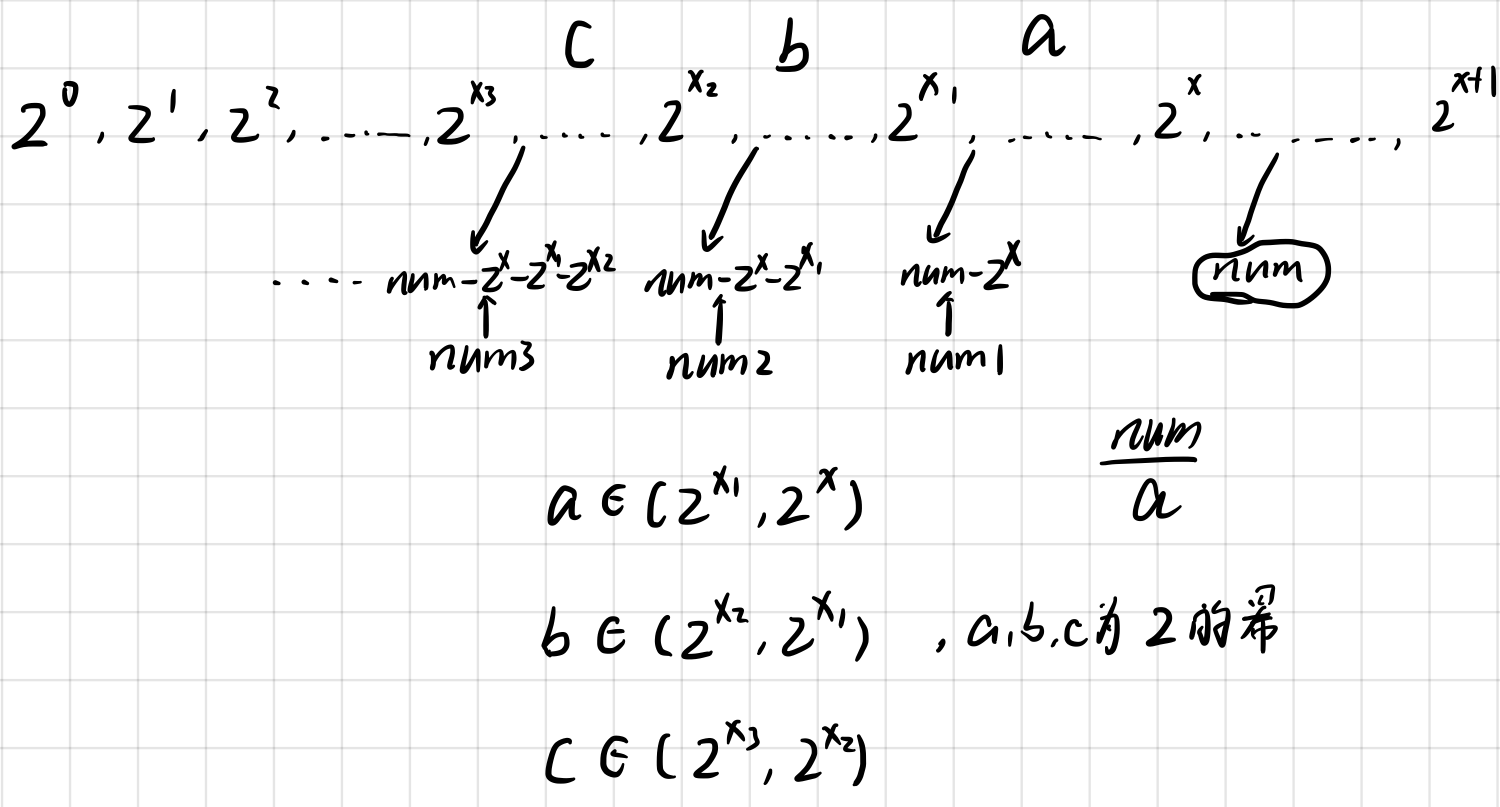Codeforces Round #529 (Div. 3) C. Powers Of Two(数学？？？？)

 

传送门

 

•题意

　　给出一个整数 n ，问能否将 n 分解成 k 个数之和，且这 k 个数必须是 2 的幂。

　　如果可以，输出"YES"，并打印出任意一组解，反之输出"NO"；

•题解

　　预备知识补充：如何求出数 num 最少需要多少个 2的幂之和？

　　例如 :

　　　　num = 3 = 2⁰+2¹至少需要两个

　　　　num = 4 = 2² 至少需要一个

　　　　num = 17 = 2⁴+2⁰ 至少需要两个

　　根据贪心的思想 :

　　　　令 2^x ≤ num，求出最大的 x ，那么此时num可以表示为 num = 2^x+num1 ( num1 = num-2^x );

　　　　num1接着重复上述过程，求出  ≤num1 的最近的2^x1，num1 = 2^x1+num2 ( num2 = num1-2^x1 );

　　　　那么num最少的2的幂之和就为 : 2^x+2^x1+2^x2+.......;

　　如何求出x,x1,x2,......呢？

　　　　　　　　2^x : ≤ num 的距num最近的2的幂

　　　　　　　　2^x1 : ≤ num1 的距num1最近的2的幂

　　　　　　　　2^x2 : ≤ num2 的距num2最近的2的幂

　　　　　　　　2^x3 : ≤ num3 的距num3最近的2的幂

　　易得 : 

　　　　(1) : num / 2^x = oddNum , num / 2^x1 = oddNum , num / 2^x2 = oddNum ,......

　　　　(2) : num / a = evenNum , num / b = evenNum , num / c = evenNum ,........

　　(1)证明 :

　　　　num / 2^x = 1;

　　　　num1 / 2^x1 = 1 → (num-2^x) / 2^x1 = 1 → num / 2^x1 - 2^x / 2^x1 = num / 2^x1 - 2^x-x1 = 1 → num / 2^x1 = 1 + 2^x-x1 = oddNum ( 奇+偶 );

　　　　num2 / 2^x2 = 1 → (num-2^x-2^x1) / 2^x2 = 1 → num / 2^x1 - 2^x / 2^x2- 2^x1 / 2^x2 = 1 → num / 2^x1 = 1 + 2^x-x2+2^x1-x2 = oddNum ( 奇+偶+偶 );

　　　　.................

　　(2)证明 :

　　　　num / a = (num1+2^x) / a = num1 / a + 2^x / a = 0+偶 = evenNum;( 2^x1 ≤ num1 < a )

　　　　..................

　　所以说：

for i:0 to k
    if(num/(2^i)为奇数)
        那么2^i就为num最少需要的2的幂之和的成员之一

　　并且，$2^i$ 等价于 两个 $2^{i-1}$，所以，可以通过 $2^i$ 转化为 $2^{i-1}$ 开填充；

•Code

#include<iostream>
#include<cstdio>
using namespace std;

int n,k;
int e[40];//e[i] : num需要e[i]个2^i

void Solve()
{
    int curK=0;
    for(int i=0;(1<<i) <= n;++i)
        if(n>>i&1)
        {
            e[i]=1;
            curK++;
        }
    //最少需要curK个2的幂
    if(k < curK || k > n)
    {
        printf("NO\n");
        return ;
    }
    printf("YES\n");
    for(int i=30;~i;--i)
    {
        if(!e[i])
            continue;
        if(curK == k)
            break;
        int x=min(e[i],k-curK);
        e[i] -= x;//减少x个2^i
        e[i-1] += 2*x;//增加2*x个2^(i-1)
        curK += x;//比之前多了x个
    }
    for(int i=0;i <= 30;++i)
        for(int j=0;j < e[i];++j)
            printf("%d ",1<<i);
}
int main()
{
    scanf("%d%d",&n,&k);
    Solve();
    return 0;
}

•感悟　　

　　其实，在比赛时，并没有做出这道题，不过也有点小想法，还不成熟；

　　赛后看排名，无意间看到了hdu大神Claris的排名，然后，看了一下Claris的提交代码，哇，真简洁，

　　是我目前无法达到的。

　　大约花费了一个多小时的时间才理解了%%%%%%%%%%%%

 

---

分割线2019.5.23

重新温习了一下这道题；

假设 n 最少由 k 个2的幂组成：

n = 2^x1 + 2^x2 +.......+ 2^xk；

那么 n / 2^xi 为奇数；

今天重新想了一下这个，没有像之前那么繁琐的推公式，一想就想到；

如果 n / 2^xi 为偶数，那么 2^xi 可以变为 2^xi+1 使得组成 n 这个幂值更大，那么，肯定比2^xi所需的2的幂少，与假设矛盾；

 

---

再次分割2019.10.24

　　二进制思想；

　　十进制数 n 对应的二进制的第 i 位如果为 1，那么 $2^i$ 就是二进制转十进制 n 的组成部分；

　　那么，也即是说，n 对应的二进制有多少个 1，n 就至少需要多少个 2 的幂之和；

　　如果这些不够 k 个，那么就通过一个 $2^i$ 可以转化为两个 $2^{i-1}$ 的形式来增加幂之和的个数；