状态压缩动态规划

　　不知不觉，状压DP已经看了有一周多时间了，上一周做了几道状压的简单题，也没整理自己的学习笔记，当然，上周比较颓废，某天晚上熬夜，直接导致接下来的两天丝毫没有学习的欲望，哎，愁人。

　　不说废话了，直奔主题：

状压DP自学笔记：

　　参考资料：

　　　　[1]:fifish (周伟，天津大学 2007级)

　　　　[2]:Tony_Double_Sky

　　预备知识：

　　　　做了几道状压的题后，在结合着大佬的博客，体会到了位运算与状压的密切联系。

　　　　像 n*n 的棋盘问题，每一个位置都可以选择放（1）还是不放（0），那么最终的状态就是 111....1 (n个1)，而我们要求的便是这n个1的方案数。

　　　　下面来补充一下位运算的知识：

　　　　其优先级为： not > and > xor > or

　　　　特别需要注意的是：== > and（踩到坑了）

　　　　

　　　　还记得树状数组中的lowbit(x)吗？

　　　　其作用就是取出x对应的二进制数中第一个 1。

　　　　例如：x=0b(1010)，lowbit(x)=x&(-x)=10;

　　　　对参考资料[1]中的引例中的一段代码的理解：

　　　　

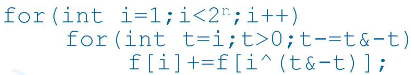
　　　　对于每一个状态 i ，其方案数为其二进制去掉任意一个 1 的所有方案总数。

　　　　例如f[100110]=f[100100]+f[100100]+f[000110];

　　　　而这段代码就是这个意思。

　　　　还是以100110为例：

　　　　　　初始,t = 100110,lowbit(t) = 10,i^lowbit(t) = 100100;

　　　　　　t -= lowbit(t) => t = 100100,lowbit(t) = 100, i^lowbit(t) = 100010;

　　　　　　t -= lowbit(t) => t = 100000,lowbit(t) = 100000, i^lowbit(t) = 000110;

　　　　还有一些比较好用的位运算，例如判断某状态 i 是否含有相邻的 1 ，则只需判断是否 i & (i << 1) == 0 即可，等等。