完全背包

https://www.cnblogs.com/violet-acmer/p/9852294.html

 自学笔记：

　　何为完全背包？

　　　　1.定义：

　　　　　　有N种物品和一个容量为V的背包，每种物品都有无限件可用。

　　　　　　第i种物品的费用是c[i]，价值是w[i]。

　　　　　　求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。 

　　　　2.与“01”背包的区别

　　　　　　“01”背包对于每个物品只有选与不选之分，而完全背包对于每个物品却有多种决策，选0,1,2,......,k个。

　　　　3.完全背包转“01”背包

　　　　　　相关变量解释：

int dp[maxn][maxn];///dp[i][j] : 前i个物品放入容量为j的背包所获得的最大价值
int w[maxn];///w[i]:第i个物品的重量
int v[maxn];///v[i] : 第i个物品的价值

　　　　　　思路：将一种物品拆成多件物品。  

　　　　　　考虑到第 i 种物品最多选 W / w[i] 件，于是可以把第 i 种物品转化为 W / w[i] 件费用及价值均不变的物品，然后求解这个01背包问题。

　　　　　　伪代码：　　　　　

for(int i=1;i <= n;++i)//物品
    for(int j=0;j <= W;++j)//容量
        for(int k=0;k*w[i] <= j;++k)//拿k个i物品
            dp[i][j]=max(dp[i-1][j],dp[i-1][j-k*w[i]]+k*v[i]);

　　　　4.完全背包

　　　　　　根据上述伪代码的循环可知

　　　　　　dp[ i ][ j ]只与dp[i-1][ j-k*w[i] ]有关，如图

                      

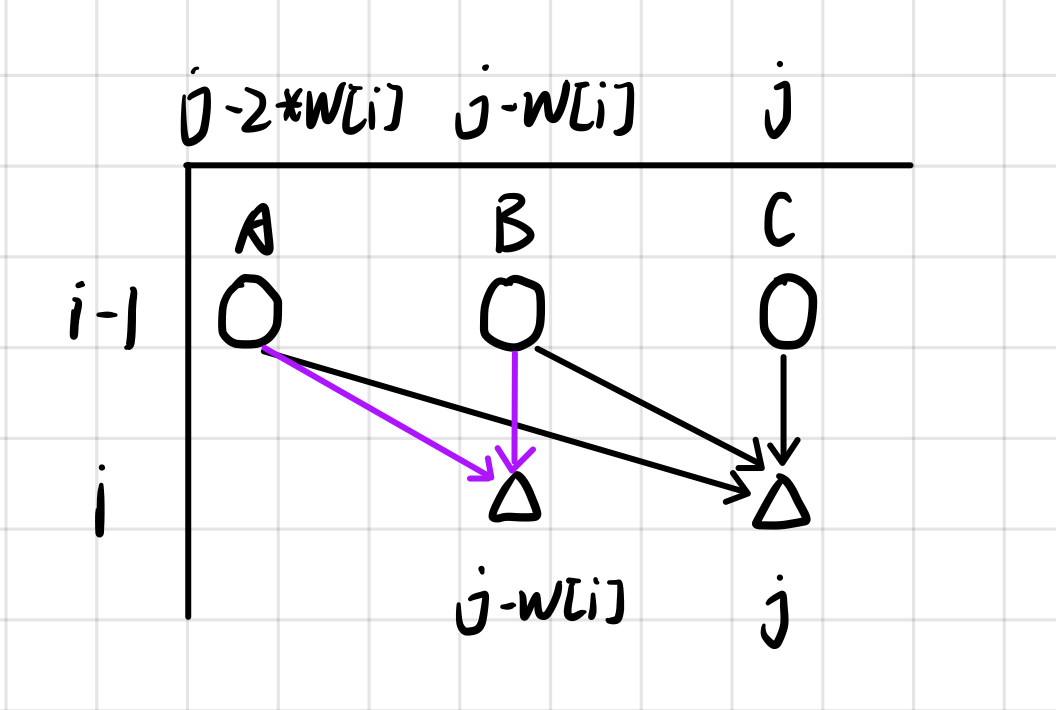
　　　　　　其中A ⇔ dp[i-1][ j-2*w[i] ]　　B ⇔ dp[i-1][ j-w[i] ]　　c ⇔ dp[i-1][ j ]

　　　　　　易得dp[i][ j-w[i] ]=max( A+v[i] , B );

　　　　　　　　dp[i][ j ]=max( A+2*v[i] , B+v[i] , C );

　　　　　　如果dp[i][ j-w[i] ]=A+v[i]，说明A+v[i] > B;

　　　　　　两边同时加上v[i]得 A+2*v[i] > B+v[i];

　　　　　　这样的话，dp[i][ j ] 得决策就变成了max( A+2*v[i] , C );

　　　　　　反之，如果dp[i][ j-w[i] ]=B，则说明B > A+v[i];

　　　　　　同理 B+v[i] > A+2*V[i];

　　　　　　那dp[i][ j ] 的决策就变成了max( B+v[i] , C );

　　　　　　综上可得dp[i][ j ]=max{ dp[i][ j-w[i] ]+v[i] , C };

　　　　　　同理，对于其余任意i,j同样成立。

　　　　　　所以，上述代码可简化为：

for(int i=1;i <= n;++i)//物品
    for(int j=0;j <= W;++j)//容量
        if(j < w[i])
            dp[i][j]=dp[i-1][j];
        else
            dp[i][j]=max(dp[i-1][j],dp[i][j-w[i]]+v[i]);

　　　　上述过程是不是用滚动数组优化空间的做法，如果使用滚动数组呢？

　　　　定义变量dp[maxn]......................dp[i] : 容量为 i 得背包所获得得最大得价值。　

for(int i=1;i <= n;++i)
    for(int j=1;j <= W;++j)
        if(j >= w[i])
            dp[j]=max(dp[j],dp[j-w[i]]+v[i]); 

　　　　你会发现，这个伪代码只与“01”背包使用滚动数组优化中 j 的循环次序不同而已。为什么这样一改就可行呢？

　　　　首先想想为什么“01”背包使用滚动数组优化中要按照 j= W down 1 的逆序来循环。

　　　　这是因为要保证第 i 次循环中的状态 dp[ i ][ j ]是由状态 dp[ i-1 ][ j-w[i] ]递推而来。

　　　　换句话说，这正是为了保证每件物品只选一次，保证在考虑“选入第i件物品”这件策略时，依据的是一个绝无已经选入第 i 件物品的子结果 dp[i-1][ j-w[i] ]。

　　　　而现在完全背包的特点恰是每种物品可选无限件，所以在考虑“加选一件第i种物品”这种策略时，却正需要一个可能已选入第 i 种物品的子结果 dp[ i ][ j-w[i] ]。

　　　　所以就可以并且必须采用 j= 1 to W 的顺序循环。

　　　　这就是这个简单的程序为何成立的道理。