链式前向星

 

参考资料：

　　[1]:https://blog.csdn.net/acdreamers/article/details/16902023

　　[2]:https://blog.csdn.net/ZHangFFYY/article/details/77871897

如果用链式前向星,就可以避免排序.

const int maxn=1e3+50;

int head[maxn];//head[i] : 表示以i为起点的第一条边存储的位置，初始化为-1
int num;//num:表示当前边在链式前向星中的编号，初始化为 0
struct Edge//边的结构体
{
    int to;//G[i].to:表示第i条边的终点
    int w;//G[i].w为边权值
    int next;//G[i].next表示与第i条边同起点的下一条边的存储位置
}G[2*maxn];//无向图需要2倍
//实际上你会发现这里的第一条边存储的位置其实就是以i为起点的所有边的最后输入的那个编号。
void addEdge(int u,int v,int w)//加边操作
{
    G[num].to=v;
    G[num].w=w;
    G[num].next=head[u];
    head[u]=num++;
}
void Prine(int u)//输出与u相关的边
{
    //~ : 按位取反，只有 ~(-1) == 0，这就是为什么初始化 head[]为-1的原因
    for(int i=head[u];~i;i=edge[i].next)
    {
        int v=edge[i].to;
        int w=edge[i].w;
        cout<<u<<"->"<<v<<' '<<w<<endl;
    }
}
void Init()//初始化操作
{
    memset(head,-1,sizeof(head));
    num=0;
}

 

 

 

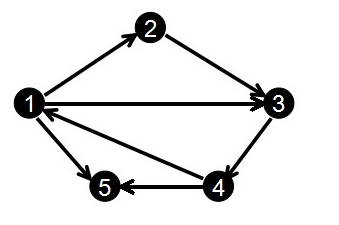
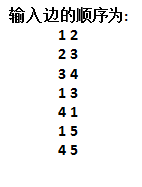
现在我们还是按照上面的图和输入来模拟一下:
G[0].to = 2;     G[0].next = -1;      head[1] = 0;
G[1].to = 3;     G[1].next = -1;      head[2] = 1;
G[2].to = 4;     G[2],next = -1;      head[3] = 2;
G[3].to = 3;     G[3].next = 0;       head[1] = 3;
G[4].to = 1;     G[4].next = -1;      head[4] = 4;
G[5].to = 5;     G[5].next = 3;       head[1] = 5;
G[6].to = 5;     G[6].next = 4;       head[4] = 6;
很明显,head[i]保存的是以i为起点的所有边中编号最大的那个,而把这个当作顶点i的第一条起始边的位置.
这样在遍历时是倒着遍历的,也就是说与输入顺序是相反的,不过这样不影响结果的正确性.
我们在遍历以u节点为起始位置的所有边的时候是这样的:
for(int i=head[u]; ~i ;i=G[i].next)//~按位取反，只有当i==-1时，~i才为0，这就是为什么初始化head[]为-1的原因,或将~i改为i != -1