LCA

 

•参考资料

　　[1]:挑战程序设计竞赛

　　[2]:Tarjan

　　[3]:郭华阳《RMQ与LCA问题》 [提取码：qvx1]

 

LCA自学笔记

何为LCA

　　在有根树中，两个节点 $u$ 和 $v$ 的公共祖先中距离根节点最远的的那个被称为最近公共祖先 (LCA,Lowest Common Ancestor)。

　　例如：

　　　　

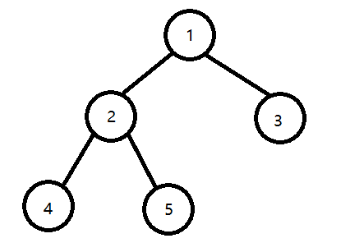
　　$LCA(4,5) = 2;$

　　$LCA(4,3) = 1;$

　　$LCA(2,5) = 2;$

基于二分的LCA

　　推荐资料：挑战程序设计竞赛（第二版）

　　1.朴素求解方式：

　　2.二分搜索优化：

　　3.模板

　　　　LCA（二分）.cpp

　　4.解惑

　　　　对模板中第 54,55,56 行的理解：

　　　　节点 v 向上走 $x=dep_v-dep_u$ 步来到和 u 同深度的位置；

　　因为 $fa[k][u]$ 存的是节点 u 向上走 $2^k$ 步来到的节点位置；

　　那么，考虑到 x 的二进制形式，如果 x 的第 i 位为 1，那么 $2^i$ 就是 x 的二进制转十进制的组成部分；

　　那么，v 肯定会向上走 $2^i$ 步，所以 $v=fa[i][v]$；

　　　　上述代码中的 54,55,56 查找 v 节点与 u 节点同一深度的祖先节点时可以优化一下（有些题因为这么一个小小的优化就过了，不然，TLE）

1 int i;
2 for(i=0;(1<<i) <= depth[v];++i);
3 i--;//从根结点(depth[root]=0)向下走，最靠近且不会超过节点v的最大步数为2^i
4 for(int k=i;k >= 0;--k)//求两者差值最少有多少个2的幂组成
5     if((depth[v]-(1<<k)) >= depth[u])//根据贪心思想，能往前走就往前走
6         v=fa[k][v];

基于Tarjan的LCA

算法流程请看参考资料[2]，下面谈谈我对此算法得理解；

对于某一结点 i ，如果询问中存在点对 $(u,v)$ 使得 $u\in i$ 的某一颗子树，$v\in i$ 的另一颗子树，那么 $LCA(u,v) = i$；

根据算法流程，由节点 i 向下搜索其中一颗子树时，假设为 u 所在的子树，但此前并没有搜索到 v 所在的子树，

当来到u节点时，此时vis[ v ] =false，并更新 fa[u]=其父亲节点,vis[u]=true；

在往上回溯过程中，再一次来到 i 节点，根据并查集可得 fa[u]=i ；

继续执行搜索过程，来到另一颗子树，假设为 v 所在的子树，当来到v节点时，vis[ u ]=true，说明之前搜索过u节点，那么

　　　　$LCA(u,v) = fa[u] = i$;

3.基于RMQ的LCA

　　1.LCA向RMQ的转化

    • 对包含 N 个节点有根树 T 进行 DFS
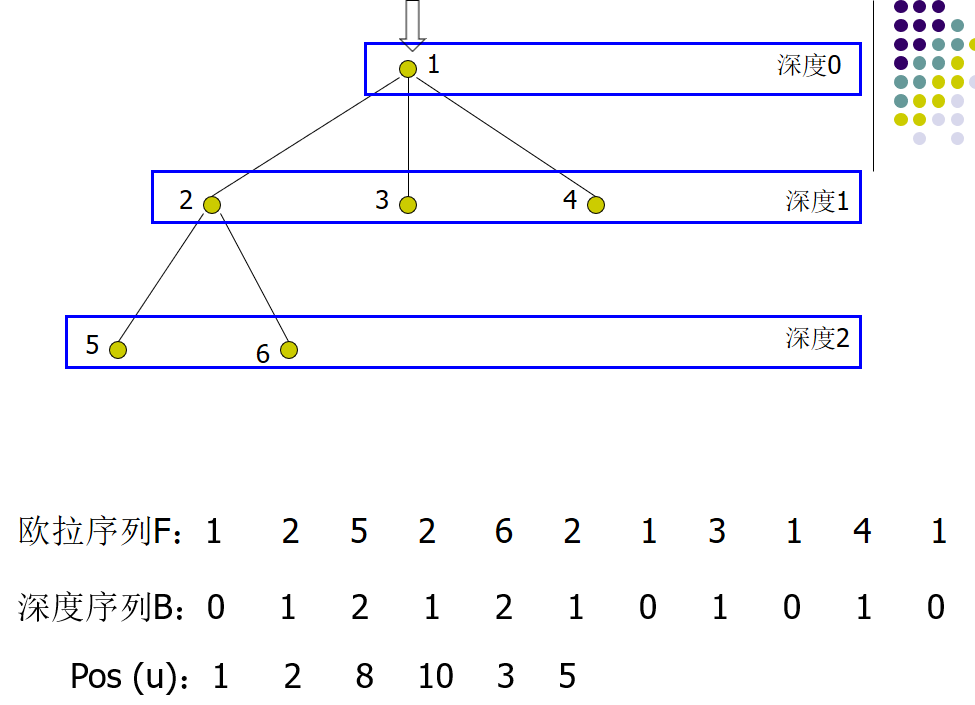
    • 将遍历到的结点按照顺序记下，我们将得到一个长度为 2N – 1 的序列，称之为 T 的欧拉序列 F
    • 欧拉序列 F 中，每个点对应一个深度，称之为 F 的深度序列
    • 每个结点都在欧拉序列中出现，我们记录结点 u 在欧拉序列中第一次出现的位置为 pos(u)
    • 图示

    • 根据DFS的性质，对于两结点u、v，从pos(u)遍历到pos(v)的过程中经过LCA(u, v)有且仅有一次
    • 且深度是深度序列B[pos(u)…pos(v)]中最小的
    • 即 $LCA(T,u,v) = RMQ(B,pos(u),pos(v))$，并且问题规模仍然是O(N)的
 1 /**
 2     LCA:DFS+ST()
 3 */
 4 #include<iostream>
 5 #include<cstdio>
 6 #include<cmath>
 7 #include<cstring>
 8 using namespace std;
 9 #define mem(a,b) memset(a,b,sizeof(a))
10 #define ll long long
11 const int maxn=1e5+50;
12 
13 int n,m;
14 int num;
15 int head[maxn];
16 ll dis[maxn];
17 struct Edge
18 {
19     int to;
20     ll w;
21     int next;
22 }G[maxn<<1];
23 void addEdge(int u,int v,ll w)
24 {
25     G[num]=Edge{v,w,head[u]};
26     head[u]=num++;
27 }
28 struct LCA
29 {
30     /**
31         个人习惯数组下标从1开始
32         此模板的下标从1开始
33     */
34     int vs[maxn<<1];///欧拉序列
35     int dep[maxn<<1];///欧拉序列对应的深度序列
36     int pos[maxn];///pos[i]:节点i在欧拉序列中第一次出现的位置
37     int cnt;
38     int logTwo[maxn<<1];///logTwo[i]=log2(i)
39     int dp[maxn<<1][20];
40     void DFS(int u,int f,int depth,ll dist)
41     {
42         vs[++cnt]=u;
43         dep[cnt]=depth;
44         pos[u]=cnt;
45         dis[u]=dist;
46         for(int i=head[u];~i;i=G[i].next)
47         {
48             int v=G[i].to;
49             int w=G[i].w;
50             if(v == f)
51                 continue;
52             DFS(v,u,depth+1,dist+w);
53             vs[++cnt]=u;
54             dep[cnt]=depth;
55         }
56     }
57     void ST()
58     {
59         ///预处理出dp[i][j],logTwo[i]
60         logTwo[0]=-1;
61         for(int i=1;i <= cnt;++i)
62         {
63             dp[i][0]=i;
64             ///111(2)->1000(2):(111)&(1000)=0,logTwo[1000]=logTwo[111]+1
65             logTwo[i]=((i&(i-1)) == 0) ? logTwo[i-1]+1:logTwo[i-1];
66         }
67         for(int k=1;k <= logTwo[cnt];++k)
68             for(int i=1;i+(1<<k)-1 <= cnt;++i)
69                 if(dep[dp[i][k-1]] > dep[dp[i+(1<<(k-1))][k-1]])
70                     dp[i][k]=dp[i+(1<<(k-1))][k-1];
71                 else
72                     dp[i][k]=dp[i][k-1];
73     }
74     void lcaInit(int root)
75     {
76         cnt=0;
77         DFS(root,root,0,0);
78         ST();
79     }
80     int lca(int u,int v)///返回u,v的公共祖先
81     {
82         u=pos[u];
83         v=pos[v];
84         if(u > v)
85             swap(u,v);
86         int k=logTwo[v-u+1];
87         if(dep[dp[u][k]] > dep[dp[v-(1<<k)+1][k]])
88             return vs[dp[v-(1<<k)][k]];
89         else
90             return vs[dp[u][k]];
91     }
92 }_lca;
93 void Init()///一定要记得Init()
94 {
95     num=0;
96     mem(head,-1);
97 }
View Code

•入门习题

题目一览表 来源         考察知识点 完成时间  
A　　2856 How far away ？ HDU 裸LCA 2018.9.21 
B　　2874 Connections between cities HDU　　 裸LCA  2018.9.22
C　　2370 小机房的树 CODEVS 裸LCA 2018.9.24
D　　1330 Nearest Common Ancestors POJ　　 RMQ&LCA入门题  2018.9.25
E　　3195 Design the city zoj LCA模板题 2018.10.8
F　　2763 Housewife Wind poj RMQ+BIT/树链剖分 2018.10.9

 

posted @ 2018-10-05 16:18  HHHyacinth  阅读(357)  评论(0)  编辑  收藏  举报