树状数组简要笔记

 

•参考资料

　　树状数组彻底入门

•简要笔记

　　　　

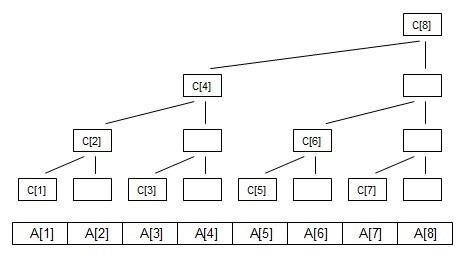
$C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8]$

$C[7]=A[7]$

$C[6]=A[5]+A[6]$

$C[5]=A[5]$

$C[4]=A[1]+A[2]+A[3]+A[4]$

$C[3]=A[3]$

$C[2]=A[1]+A[2]$

$C[1]=A[1]$

　　你会发现，$C[x]$ 的取值和线段树中，去掉所有的右儿子后，以 $x$ 为结尾的区间包含的数相同；

　　$lowbit(x)$ : 取出 $x$ 的最低位 1；

　　$lowbit((1010)_2)=(10)_2$

　　$lowbit((1101)_2)=(1)_2$

　　并且有 $C[x]=A[x]+A[x-1]+\cdots +A[x-lowbit(x)+1]$；

　　就是，与 $x$ 末尾连续 0 的个数有关系；

　　$sum[7]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]=C[4]+C[6]+C[7]$；

　　转化成二进制就是：

　　　　$sum[(111)]=C[(111)]+C[(110)]+C[(100)]$；

　　每次都会去掉低位的 1；

　　也就是 $x -= lowbit(x)$ 操作；