动态规划之最大M子段和问题

 

自学笔记

•参考资料

　　[1]:最大m子段和总结与例题 51nod1052 HDU1024

•何为最大M子段和？

• 给定由 n 个整数（可能为负）组成的序列 $a_1,a_2,\cdots ,a_n$ 以及一个正整数m
• 求序列的 m 个不相交子段，使这 m 个子段的总和最大

　　特别注意：

　　　　有些题目可能不需要必须找到 m 个子段，例如给出的序列中，正整数个数不足 m 个，那么答案是所有正整数的加和。

　　　　此时选择的子段个数是全部的正整数个数，不足 m 个，但符合题意，如这道题【51nod 1052 最大M子段和】

　　　　也可能有些题目要求，必须选够 m 个子段，如这道题【HDU 1024】。

•问题的解

　　动态规划，借助矩阵可以直观的看到计算过程。

　　定义二维数组 $dp$， $dp[i][j]$，表示前 j 项所构成 i 子段的最大和，且必须包含着第 j 项，即以第 j 项结尾；

　　求 $dp[i][j]$，有两种情况：

• • $dp[i][j]=max(dp[i][j],dp[i][j-1]+a[j])$ ，即把第 j 项融合到第 j-1 项的子段中，子段数没变
  • $dp[i][j]=max(dp[i][j],dp[i-1][k]+a[ j ])\ ,\ (i-1\leq k < j)$，即第 j 项单独作为一个子段加入到前 j-1 个形成的 i-1 个子段中；

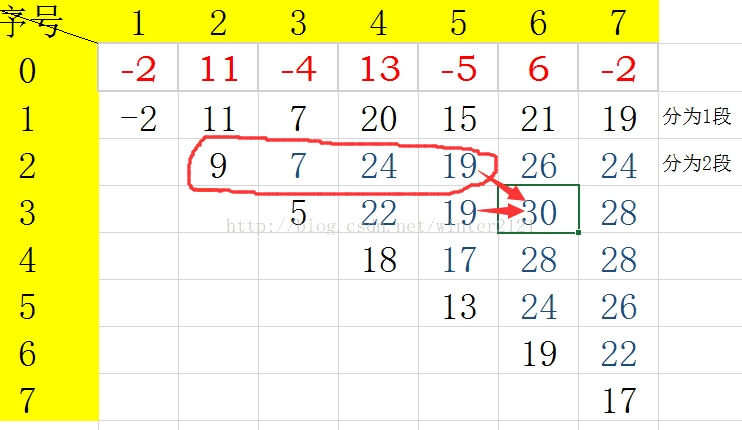
　　如图所示，红色数字为输入的序列：

 

　　如图，要求 $dp[3][6]$，只需比较他左边的那个，和上面那一行圈起来的之中最大的数+$a_j$ 即可；

　　优化：

• • 沿着第 m 行的最后一个元素，往左上方向画一条线，线右上方的元素是没必要计算的
  • 因为线右上方的元素没必要计算，所以，在计算第 $i$ 行的 $dp[i][j]$ 时，$j$ 的范围为 $[i,n-m+i]$
  • 左下角那一半矩阵，也是不用计算的，因为分成 $i$ 段至少需要 $i$ 个数字
  • 每确定一个 $dp[i][j]$，只需用到本行和上一行，所以不用开二维数组也可以，省内存

•Code

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define INFll 0x3f3f3f3f3f3f3f3f
#define mem(a,b) memset(a,b,sizeof(a))
const int maxn=1e6+50;

int n,m;
ll a[maxn];
ll dp[maxn];
ll Max[maxn];

ll Solve()
{
    /**
        二位数组中，dp[i][j]的求解依赖 dp[i][j-1] 以及 max(dp[i-1][j-1],dp[i-1][j-2],...,dp[i-1][i-1])
        因为只需要当前行和上一行的最大值
        所以，我定义 Max[j] 表示前一行中[i-1,j]的dp最大值
    */
    mem(Max,0);
    for(int i=1;i <= m;++i)
    {
        dp[i-1]=-INFll;///i-1个数不能划分成i段，所以将dp[i-1]赋值为-INFll
        for(int j=i;j <= n-m+i;++j)
            dp[j]=max(dp[j-1],Max[j-1])+a[j];
            
        Max[i-1]=-INFll;///i-1个数不能划分成i段，所以将Max[i-1]赋值为-INFll
        for(int j=i;j <= n-m+i;++j)
            Max[j]=max(Max[j-1],dp[j]);
    }
    return *max_element(dp+m,dp+n+1);
}

 

---

 

HDU1024

•题意

　　给你 n 个数，将这 n 个数恰好划分成 m 个互不相交的子段，求这 m 个子段的最大值；

•题解

　　因为题目让求的是恰好 m 个互不相交的子段，那么，势必有 $m \le n$，不然是无法满足题意的；

　　直接按照上述分析的更新 m 次 $dp$ 值即可，最后，输出 $max(dp_m,dp_{m+1},\cdots ,dp_n)$ 即可；

•Code

　　HDU1024.cpp

 

---

 

51nod 1052

•题解

　　相比上一题，这道题的要求如果正整数的个数不足 m 个，直接输出这些正整数的加和即可；

　　只需要在上一题的基础上增加一个特判即可；

•Code

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define INFll 0x3f3f3f3f3f3f3f3f
#define mem(a,b) memset(a,b,sizeof(a))
const int maxn=5e3+50;

int n,m;
ll a[maxn];
ll dp[maxn];
ll Max[maxn];

ll Solve()
{
    ll sum=0;
    int cnt=0;
    for(int i=1;i <= n;++i)
        if(a[i] > 0)
        {
            sum += a[i];
            cnt++;
        }
    if(m >= cnt)
        return sum;

    for(int i=1;i <= m;++i)
    {
        dp[i-1]=-INFll;
        for(int j=i;j <= n-m+i;++j)
            dp[j]=max(dp[j-1],Max[j-1])+a[j];
        Max[i-1]=-INFll;
        for(int j=i;j <= n-m+i;++j)
            Max[j]=max(Max[j-1],dp[j]);
    }
    return *max_element(dp+m,dp+n+1);
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i <= n;++i)
        scanf("%lld",a+i);
    printf("%lld\n",Solve());

    return 0;
}