初始线性基
•参考资料
[1]:百度百科
[2]:算法 | 线性基学习笔记
[4]:异或线性基分析
•学习历程
- 通过资料[1],明白了线性基的用途
- 通过资料[2],掌握了线性基的构造、查询、合并
- 大致掌握后,做了做相关习题 BZOJ 2460 并参阅了资料[3]
- 看到这道题 CF 1100F 时,写了个线性基+线段树的代码,TLE,不过学会了如何让线性基与线段树结合
- 之后,便是疯狂的找题解,终于,看到了这篇--资料[4],有关线性基的分析写的很好,让我深入理解了线性基的构造,查询
- 结合着资料[4],[5]顺利AC这道题
•习题集锦
线性基进阶--线性基求交
•参考资料
[1]:线性基求交
[2]:2019牛客多校第四场题解
[3]:线性基求交
[4]:线性基学习笔记
•备注
以下解析摘抄自资料[4],博主讲解的很明白,tql;
•何为线性基的交?
假设求交的对象是两组线性基 $A,B$
求线性基交,是指求一组新的线性基 $C$,使得任意能被 $C$ 表示的数都能被线性基 $A,B$ 表示;
且不能被 $C$ 表示的数也不能被线性基 $A,B$ 同时表示;
•引理
设线性基 $A$ 所对应的线性空间为 $V_A$(就是 $A$ 能表示的所有数的集合),线性基 $B$ 所对应的线性空间为 $V_B$;
令 $W=V_A\cap B$(即 $W$ 是线性基 $B$ 中能被 $A$ 表示的基向量的集合)
则有定理:若 $A\cup (B-W)$ 线性无关,那么 $W$ 就是我们所想求的 $A,B$ 的线性基交;
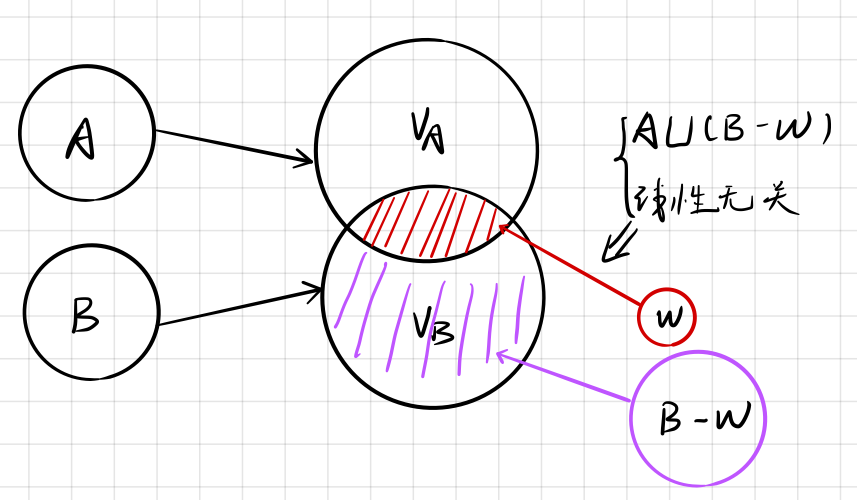
•引理的图解证明
$A\cup (B-W)$ 线性无关,也就是说 基$B-W$ 对应的线性空间与 基$A$ 对应的线性空间没有交集;
也就是 基$B-W$ 对应的线性空间为上图紫色区域,那么,基$W$ 对应的线性空间就为 $V_A\cap V_B$ 所对应的区域;
•解的可行性
但是我们不能保证对于线性空间 $V_B$ 的任意一组线性基 $B$,都有 $A\cup (B\setminus W)$ 线性无关;
比如,想对 $A=\{5\},B=\{1,4\}$ 求线性基交,显然结果是 $C=\{5\}$;
但是按照上述解法,令 $W=V_A\cap B = \phi$,$A\cup (B-W) = \{1,4,5\}$ 线性相关,所以此时求解的 基$W$ 并非答案;
于是我们所需要做的,就是调整出一组线性基 $B'$(记 $W'=V_A\cap B'$),使得 $A\cup (B'- W')$ 线性无关;
还是上面的例子,我们可以调整出 $B'=\{1,5\}$,这样一来线性空间 $V_B$ 不变,同时能顺利求出线性基交 $C$;
•实现流程
我们可以动态地维护一个线性基 $all$,$all=A\cup (B'-W')$;
表示尝试插入当前 $B$ 中基向量 $B_i$ 后,$A\cup (B'- W')$ 所对应的线性基;
初始,$all=A\ ,\ B'=\phi \ ,\ W'=\phi$;
我们依次将 $B$ 中的基向量尝试插到 $all$ 中(从高位到低位、从低位到高位皆可),假设当前插入 $B_i$:
1. $B_i$ 能够插进$all$中,这意味着 $B_i$ 与当前的 $all$ 线性无关,那么显然 $B_i\notin W'$,$B_i \in B'$;
2. $B_i$ 不能插进$all$中,这意味着 $B_i$ 可以通过 $all$ 表示,那么 $B_i \notin all$;
并需要进行调整、使得调整后的 $B_i \in W'$;
(1) 若 $B_i$ 只用 $A$ 即可表示,那么无需调整,$B_i \in W'$;
(2) 若 $B_i$ 需要 $A$ 及 $B'_{p_1},B'_{p_2},...,B'_{p_m}$ 才能表示;
那么我们考虑 $u=B_i\ xor\ B'_{p_1}\ xor\ ...\ xor\ B'_{p_m}$;
显然,这时 $u$ 只用 $A$ 就可以表示了;
经过这样的调整后,就有 $u \in W$;
•Code