求无向连通图的割点
参考资料:
[1]: 【图论】求无向连通图的割点
[2] : 深度优先生成树及其应用
1.割点与联通度
在无向连通图中,删除一个顶点v及其相连的边后,原图从一个连通分量变成了两个或多个连通分量,则称顶点v为割点,同时也称关节点(Articulation Point)。
一个没有关节点的连通图称为重连通图(biconnected graph)。
若在连通图上至少删去 k 个顶点才能破坏图的连通性,则称此图的连通度为k。
2.简单的例子
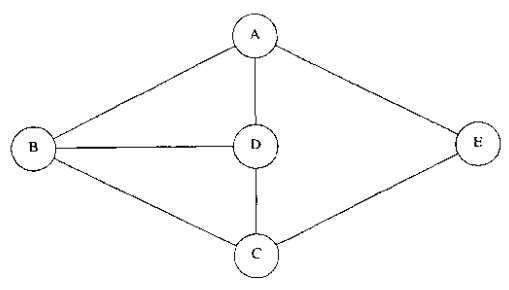
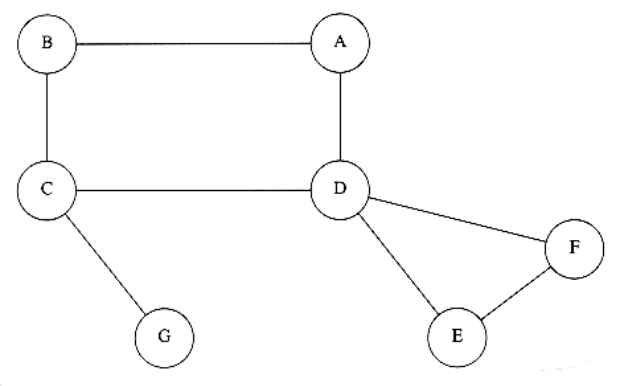
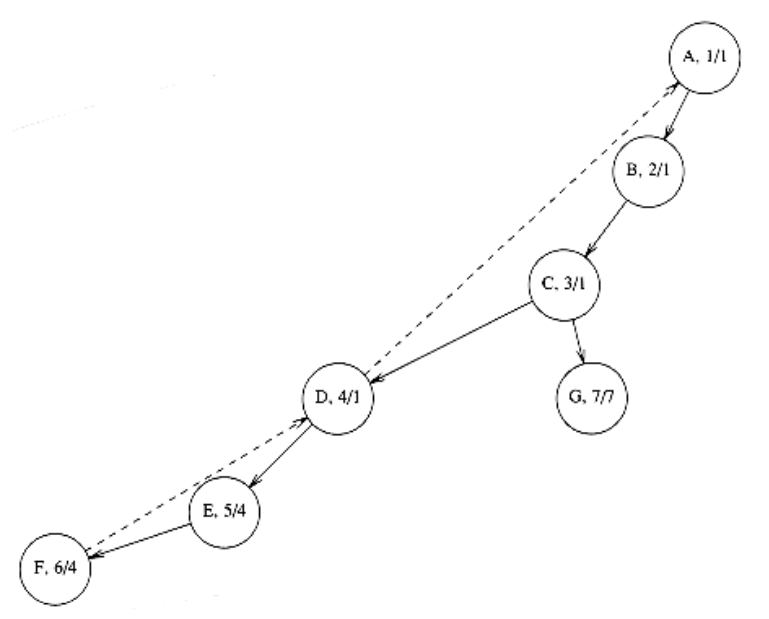
(图a) (图b) (图c)
图a为重联通图,图b为非重联通图;
图b的割点为 C,D;
3.高效求解割点的方法
在介绍算法之前,先介绍几个基本概念
- DFS搜索树:用DFS对图进行遍历时,按照遍历次序的不同,我们可以得到一棵DFS搜索树,如图(c)所示,(以图b的A为根节点)。
- 树边:(也称为父子边),在搜索树中的实线所示,可理解为在DFS过程中访问未访问节点 时所经过的边。
- 回边:(也称为返祖边、后向边),在搜索树中的 虚线 所示,可理解为在DFS过程中遇到 已访问节点 时所经过的边。
该算法是R.Tarjan发明的。观察DFS搜索树,我们可以发现有两类节点可以成为割点:
- 对根节点u,若其有两棵或两棵以上的子树,则该根结点 u 为割点;
- 对非叶子节点 u(非根节点),若其子树的节点均没有指向 u 的祖先节点的回边,说明删除u之后,根结点与u的子树的节点不再连通;则节点u为割点。
对于根结点,显然很好处理;但是对于非叶子节点,怎么去判断有没有回边是一个值得深思的问题。
我们用dfn[u]记录节点u在DFS过程中被遍历到的次序号,low[u]记录节点u或u的子树通过非父子边追溯到最早的祖先节点(即DFS次序号最小);
那么low[u]的计算过程如下:
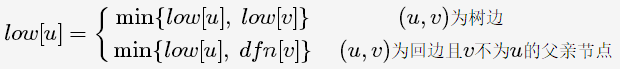
对于情况2,当(u,v)为树边且 low[v] >= dfn[u]时,节点u才为割点。
该式子的含义:以节点v为根的子树所能追溯到最早的祖先节点要么为 v 要么为 u。
参考代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 using namespace std; 5 #define mem(a,b) memset(a,b,sizeof(a)) 6 const int maxn=1e3+50; 7 8 int n,m; 9 int fa[maxn]; 10 int dfn[maxn]; 11 int low[maxn]; 12 int root; 13 bool vis[maxn]; 14 bool artPoint[maxn];//判断节点i是否为割点 15 int num; 16 int head[maxn]; 17 struct Edge 18 { 19 int to; 20 int next; 21 }G[2*maxn]; 22 void addEdge(int u,int v) 23 { 24 G[num].to=v; 25 G[num].next=head[u]; 26 head[u]=num++; 27 } 28 29 void DFS(int u,int f,int &k,int &rootSon) 30 { 31 fa[u]=f; 32 vis[u]=true; 33 dfn[u]=low[u]=++k; 34 if(f == root) 35 rootSon++; 36 for(int i=head[u];~i;i=G[i].next) 37 { 38 int v=G[i].to; 39 if(!vis[v])//父子边 40 { 41 DFS(v,u,k,rootSon); 42 43 if(low[v] >= dfn[u] && u != root) 44 artPoint[u]=true; 45 46 low[u]=min(low[u],low[v]); 47 } 48 else if(fa[u] != v)//返祖边 49 low[u]=min(low[u],dfn[v]); 50 } 51 } 52 int Solve() 53 { 54 int k=0; 55 root=1;//以任意合法的节点为根节点都可以 56 int rootSon=0;//根节点的儿子个数 57 DFS(root,-1,k,rootSon); 58 59 int ans=0; 60 for(int i=1;i <= n;++i) 61 ans += artPoint[i] ? 1:0; 62 ans += rootSon >= 2 ? 1:0; 63 return ans; 64 } 65 void Init() 66 { 67 num=0; 68 mem(head,-1); 69 mem(vis,false); 70 mem(artPoint,false); 71 } 72 int main() 73 { 74 //n个节点,m条边 75 while(~scanf("%d%d",&n,&m)) 76 { 77 Init(); 78 for(int i=1;i <= m;++i) 79 { 80 int u,v; 81 scanf("%d%d",&u,&v); 82 addEdge(u,v); 83 addEdge(v,u); 84 } 85 printf("此图的割点个数为:%d\n",Solve()); 86 } 87 return 0; 88 }
以上内容全部参考自大佬博客,下面谈谈我的心得:
1.问法不同,定义的变量artPoint的状态就不同
[1]:如果题目求得是割点的个数或者只让求出那些点是割点,那么,artPoint定义成bool型的就可以了。
[2]:如果题目让求出删除某个割点所形成的联通子图的数量呢?这该怎么做呢?(poj 1523"SPF")
答案是将artPoint定义成int型的,然后,将44行的语句 artPoint[u]=true 改成 artPoint[u]++即可,对于非根节点的割点 u ,将
其删去后,会形成 artPoint[ u ]+1个联通子图。
为什么这么做会对呢?
对于这么一个图a
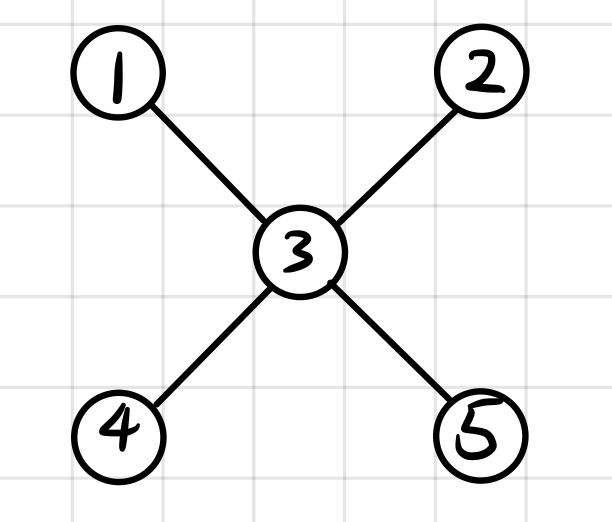
图a 图b
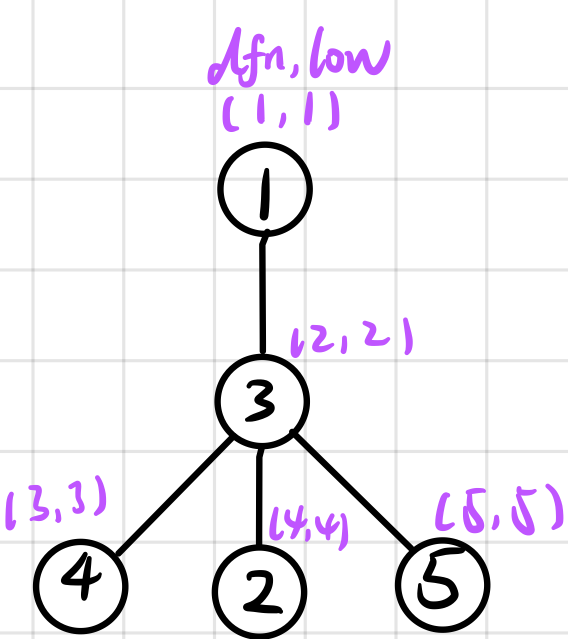
其形成的深度优先生成树为图b;
显然,artPoint[3]=3,artPoint[3]+1就是将割点3删去后的联通子图的个数,那,如果④和⑤有边相连呢(图c)?
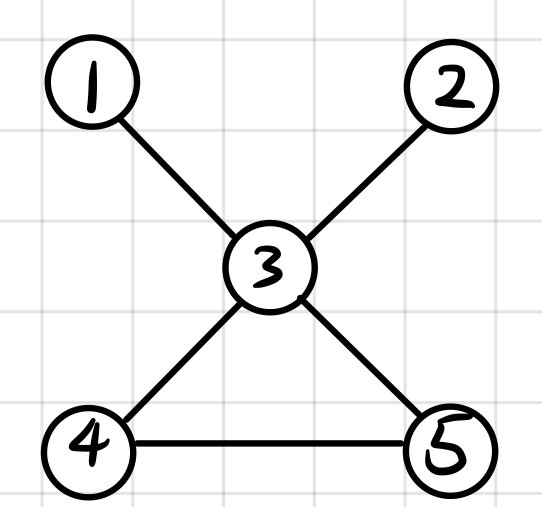
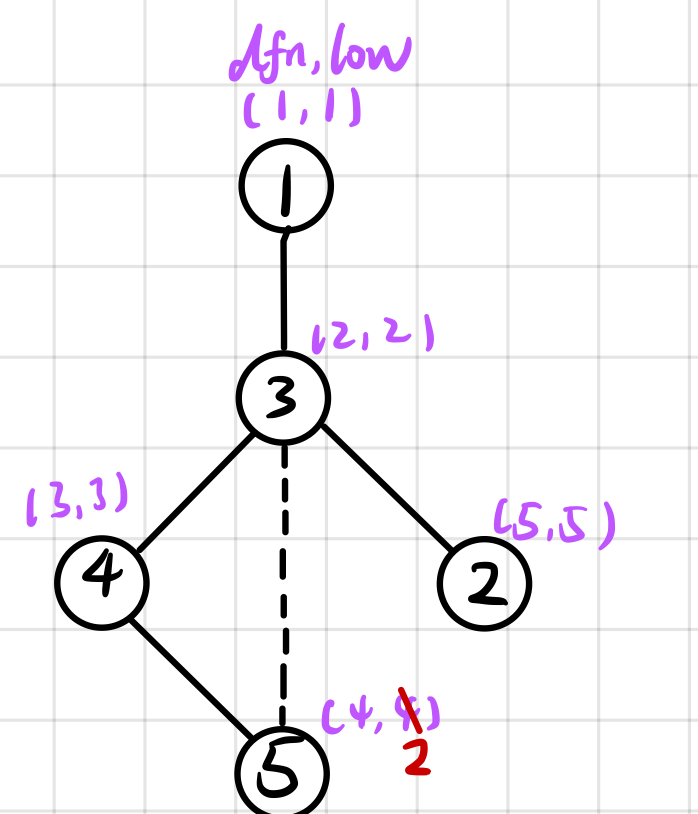
图c 图d
根据深度优先生成树的顺序,假设③节点先来到④节点,那么接下来的操作一定为DFS(4,5,k,rootSon),那么形成的深度优先生成树为图d;
那么,当来到节点④时,由于low[5] < dfn[4]所以④不再是割点,那么最后求出的artPoint[3]=3;
artPoint[3]+1还是删去割点3后形成的联通子图的个数。
2.求解任意两点间的割点个数呢?([蓝桥杯][2013年第四届真题]危险系数)
具体戳这里👉解题报告
以上为目前的解题心得,持续更新中~~~~~~~




