拓展KMP

 

•参考资料

　　[1]:刘雅琼PPT讲义 [提取码：337l]

　　[2]:kuangbin的模板

•问题描述

　　给定母串S，和子串T。
　　定义 n = |S| , m = |T|，extend[ i ] = S[ i..n-1 ]与T[0...m-1] 的最长公共前缀长度。

　　请在线性的时间复杂度内，求出所有的 extend[ 0..n-1 ]。

　　注意：字符串下标从0开始

•解释

　　

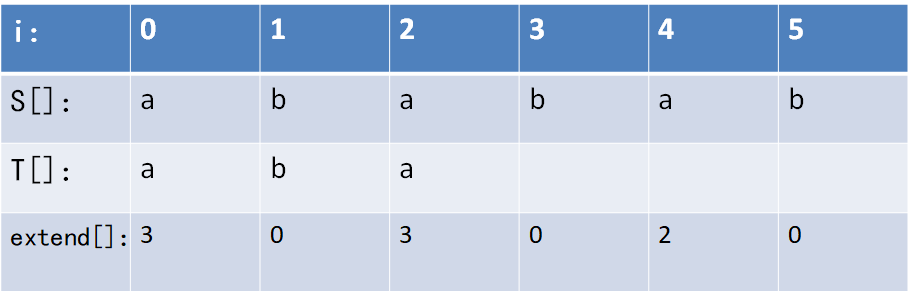
　　n = |S| = 6 , m = |T| = 3;

　　extend[0] = S[0….n-1]与T[0...m-1]的最长公共前缀，为aba，故extend[0] = 3。
　　extend[1] = S[1….n-1]与T[0...m-1]的最长公共前缀，无，故extend[0] = 0。
　　extend[2] = S[2….n-1]与T[0...m-1]的最长公共前缀，为aba，故extend[0] = 3。
　　以此类推…………

•问题的解

　　容易发现，如果有某个位置 i 满足 extend[ i ] = m；

　　那么 T 就肯定在 S 中出现过，并且进一步知道出现首位置是 i，而这正是经典的KMP问题。
　　例如：对上述样例分析，当 i = 0 时，extend[0] = 3，而 |T|=3，满足上述描述。
　　因此可见“扩展的KMP问题”是对经典KMP问题的一个扩充和加难。

　　

　　　　　　　　　　　　　（红色字母表示失配，在第10位置失配）

　　这里为了要计算extend[0]，需要进行11次比较运算，求出extend[0]=10。

　　然后计算 extend[1] = 9；

　　为了计算 extend[1]，我们是不是也要进行10次比较运算呢？
　　答案当然是否定的，因为通过计算 extend[0]=10，我们可以得到这样的信息：
　　　　S[0..9] = T[0..9];
　　　　S[1..9] = T[1..9];
　　计算 extend[1] 的时候，实际上是 S[1] 开始匹配 T[0...m-1]。

　　因为 S[1..9] = T[1..9]，所以在匹配的开头阶段是 “以 T[1..9] 为母串，T为子串” 的匹配。

　　设辅助函数 next[ i ] 表示 T[ i..m-1 ]与 T[0...m-1] 的最长公共前缀长度。
　　对上述例子，next[1] = 10，也就是说：

　　　　①T[1..10]=T[0..9];
　　　　②T[1..9]=T[0..8];
　　由 ①② 可推出 S[1..9] = T[1..9] = T[0..8] 。
　　这就是说前9位的比较是完全可以避免的！

　　我们直接从 S[10] ? T[9] 开始比较。

　　这时候一比较就发现失配，因此extend[1]=9。

•拓展KMP算法

　　下面提出一般的算法。
　　定义P：在匹配 extend[ i ] 时，i 之前已匹配的最远的公共前缀，即 $P=\sum_{j=0}^{j<i}max\{extend_j\}$；

　　设取最大值的 j 用字母 K 表示，即P = extend[ k ]。

　　假设 extend[ 0…i ] 已经计算好，并且在之前的匹配过程中到达的最远位置为 P，取到最远位置 P 的下标为 K。
　　

　　根据定义：S[ K....P ] = T[ 0….P-K ] ⇔ S[ i+1...P ] = T[ i+1-K...P-K];
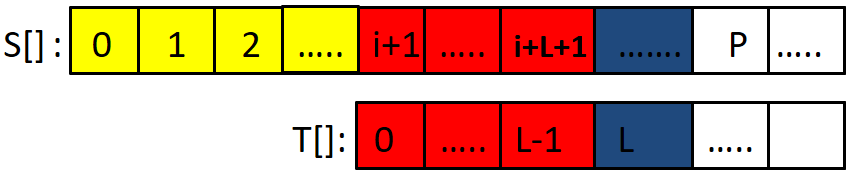
　　设 L = next[ i+1-K ]，则T[ i+1-K...L+(i+1-K)-1] = T[ 0...L-1 ];

　　情况①：P-K ≥ L+(i+1-K)-1，即 P ≥ L+i，也就是说从 S[ i+1 ] 开始匹配，只匹配到了 T[ 0...L-1 ]，如下图：

　　　　

　　　　上面红色部分代表相等部分，蓝色部分肯定不相等。
　　　　因为 next[ i+1-K ] = L，如果蓝部分相等的话，next[ i+1-K ] 必定大于 L，而所求的next[]是正确的，与此矛盾；
　　　　这个时候无需任何比较就得 extend[ i+1 ] = L，且不必更新 P,K； 
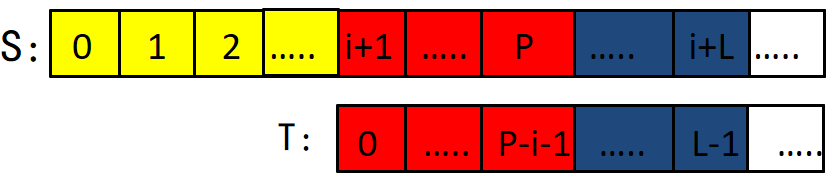
　　情况②：P-K < L+(i+1-K)-1，也就是说从 S[ i+1 ] 开始匹配，目前匹配到了 T[ 0...P-i-1 ]，如下图：

　　　　

　　　　上图蓝色部分是未知的，因为在计算extend[0...i]时，达到的最远位置为 P，所以P之后未被访问过。
　　　　这种情况下，就要从S[ P+1 ] ？ T[ P-i ] 开始匹配，直到失配为止，匹配完后，更新 P , K。

•Code

char T[maxn];//母串，长度为 n
char S[maxn];//子串，长度为 m
int nex[maxn];//S[i...m-1]与S[0...m-1]的最长公共前缀
int extend[maxn];//T[i,...,n-1]与S[0,...,m-1]的最长公共前缀
void getNex
{
    int len=strlen(S);
    nex[0]=len;
    int j=0;
    while(j+1 < len && S[j+1] == S[j])
        j++;
    nex[1]=j;
    int k=1;
    for(int i=2;i < len;++i)
    {
        int P=k+nex[k]-1;
        int L=nex[i-k];
        if(L < P-i+1)
            nex[i]=L;
        else
        {
            int j=max(0,P-i+1);
            while(j < len && i+j < len && S[j] == S[i+j])
                j++;
            k=i;
            nex[i]=j;
        }
    }
}
void getExtend()
{
    int len1=strlen(T);
    int len2=strlen(S);
    int j=0;
    while(j < len1 && j < len2 && T[j] == S[j])
        j++;
    extend[0]=j;
    int k=0;
    for(int i=1;i < len1;++i)
    {
        int P=k+extend[k]-1;
        int L=nex[i-k];
        if(L < P-i+1)
            extend[i]=L;
        else
        {
            int j=max(0,P-i+1);
            while(i+j < len1 && j < len2 && T[i+j] == S[j])
                j++;
            k=i;
            extend[i]=j;
        }
    }
}