支配集,覆盖集与独立集与匹配
参考资料:
本讲内容会涉及以下容易相互混淆的内容:
- 点支配集, 极小点支配集, 最小点支配集, 点支配数γ0(G);
- 点独立集, 极大点独立集, 最大点独立集, 点独立数β0(G);
- 点覆盖集, 极小点覆盖集, 最小点覆盖集, 点覆盖数α0(G);
- 边覆盖集, 极小边覆盖集, 最小边覆盖集, 边覆盖数α1(G);
- 边独立集(匹配), 极大边独立集(极大匹配), 最大边独立集(最大匹配), 边独立数(或匹配数)β1(G);
以上几个量存在以下关系:
α0 + β0 = n,即:点覆盖数 + 点独立数 = n;
α1 + β1 = n,即:边覆盖数 + 边独立数 = n;
首先看一下他们的的定义:

定义1:支配与支配集
设图G = <V, E>, V* ⊆ V, 若对于 ∀vi ⊆ (V - V*), ∃vj ⊆ V*,使得(vi, vj) ⊆ E, 则称 vj 支配 vi , 并称V*为G的一个支配集;
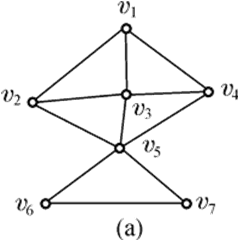
图(a)中,V*={ v1, v5 }就是一个支配集。
因为V-V*={v2, v3, v4, v6, v7}中的顶点都是V*中顶点的邻接顶点。
通俗地讲,所谓支配集,就是 V 中的顶点要么是 V* 集合中的元素,要么与 V* 中的一个顶点相邻。
若支配集 V* 的任何真子集都不是支配集, 则称V*是极小支配集;
顶点数最少的支配集称为最小支配集;
最小支配集中的顶点数称为支配数, 记作γ0(G)或简记为γ0。
图(a)中, { v1, v5 }, { v3, v5 }和{ v2, v4, v7 }都是极小支配集,{ v1, v5 }, { v4, v5 }和{ v3, v6 }都是最小支配集, γ0 = 2。
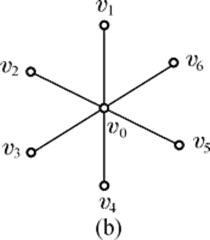
图(b)为7阶星形图, { v0 }, { v1, v2, ..., v6 }为极小支配集,{ v0 }为最小支配集, γ0 = 1。
图(c)为轮图W6,{ v0 }, { v1, v3 }, { v1, v4 }等都是极小支配集, 显然, γ0=1。
支配集的性质:
若G中无孤立顶点(度数为0的顶点),则存在一个支配集V*,使得G中除V*外的所有顶点也组成一个支配集(即V - V*也是一个支配集)。
若G中无孤立顶点(度数为0的顶点),V1*为极小支配集,则G中除V1*外的所有顶点也组成一个支配集(即V – V1*也是一个支配集)。



定义2:覆盖与点覆盖集
设G = <V, E>, V* ∈ V, 若对于"∀e ∈ E, ∃v ∈ V*, 使得v与e相关联,则称v覆盖e,并称V*为G的点覆盖集或简称点覆盖;
图(a)中,V*= { v1, v3, v5, v7 }就是一个点覆盖集。
通俗地讲,所谓点覆盖集V*,就是G中所有的边至少有一个顶点属于V*(顶点覆盖边)。
若点覆盖V*的任何真子集都不是点覆盖, 则称V*是极小点覆盖;
顶点个数最少的点覆盖称为最小的点覆盖;
最小点覆盖的顶点数称为点覆盖数, 记作α0(G), 简记为α0。
图(a)中, { v2, v3, v4, v6, v7 }, { v1, v3, v5, v7 }等都是极小点覆盖,,{ v1, v3, v5, v7 }是最小点覆盖,α0 = 4;
图(b)中, { v0 }, { v1, v2, …, v6 }都是极小点覆盖,,{ v0 }是最小点覆盖,α0 = 1;
图(c)中, { v0, v1, v3, v4 }, { v0, v1, v3, v5 }都是极小点覆盖,也都是最小的点覆盖,α0 = 4。



定义3:点独立集
对于图G=(V,E)来说,最大独立集指的是从V中取尽量多的点组成一个集合,使得这些点之间没有边相连。
也就是说,设V’是图G的一个独立集,则对于图中任意一条边(u,v),u和v不能同时属于集合V',甚至可以u和v都不属于集合V‘。
如果在V’中添加任何不属于V‘的元素后V’不再是独立集,则称V‘是极大独立集。
称G的所有顶点独立集中顶点个数最多的独立集为最大独立集。
对于任意图G来说,这三个问题不存在多项式时间的解法。
不过对于树来说,却很容易。
目前有两种解法,一种基于贪心思想,另一种基于树形动态规划思想。
一:贪心法
以最小支配集为例,对于树上的最小支配集问题,贪心策略是首先选择一点为根,按照深度优先遍历得到遍历序列;
按照所得序列的反向序列的顺序进行贪心,对于一个既不属于支配集也不与支配集中的点相连的点来说,
如果他的父节点不属于支配集,将其父节点加入支配集。
这里注意到贪心的策略中贪心的顺序非常重要,按照深度优先遍历得到遍历序列的反向进行贪心,
可以保证对于每个点来说,当其子树都被处理过后才轮到该节点的处理,保证了贪心的正确性。
最小点覆盖和最大独立集与上面的做法相似。
对于最小点覆盖来说,贪心的策略是:
如果当前点和当前点的父节点都不属于顶点覆盖集合,则将父节点加入到顶点覆盖集合,并标记当前节点和其父节点都被覆盖。
对于最大独立集来说,贪心策略是:
如果当前点没有被覆盖,则将当前节点加入到独立集,并标记当前节点和其父节点都被覆盖。
需要注意的是由于默认程序中根节点和其他节点的区别在于根节点的父节点是其自己;
所以三种问题对根节点的处理不同:对于最小支配集和最大独立集,需要检查根节点是否满足贪心条件,但是对于最小点覆盖不可以检查根节点。
因为fa[root]=root,当来到root点时,root点肯定不会出现在最小点覆盖集合里,那么fa[root]也不会出现在最小点覆盖集合里,
贪心代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 using namespace std; 5 #define mem(a,b) memset(a,b,sizeof(a)) 6 const int maxn=1e5+50; 7 8 int n; 9 int num; 10 int head[maxn]; 11 struct Edge 12 { 13 int to; 14 int next; 15 }G[2*maxn]; 16 int fa[maxn];//父节点 17 int vs[maxn];//深度优先搜索序列 18 bool domSet[maxn];//最小支配集(dominate) 19 bool covSet[maxn];//最小点覆盖(cover) 20 bool indSet[maxn];//最大独立集(independent) 21 bool vis[maxn];//vis[i]:判断节点i是否与集合中的节点有关联 22 void addEdge(int u,int v) 23 { 24 G[num].to=v; 25 G[num].next=head[u]; 26 head[u]=num++; 27 } 28 void Dfs(int u,int f,int &k) 29 { 30 fa[u]=f; 31 vs[++k]=u; 32 for(int i=head[u];~i;i=G[i].next) 33 { 34 int v=G[i].to; 35 if(v == f) 36 continue; 37 Dfs(v,u,k); 38 } 39 } 40 //求解最小支配集 41 int DomSet(int k) 42 { 43 mem(vis,false); 44 int ans=0; 45 for(int i=k;i >= 1;--i) 46 { 47 int v=vs[i]; 48 int f=fa[v]; 49 if(!vis[v]) 50 { 51 if(!domSet[f]) 52 { 53 domSet[f]=true; 54 ans++; 55 } 56 vis[v]=true; 57 vis[f]=true; 58 vis[fa[f]]=true; 59 } 60 } 61 return ans; 62 } 63 //求解最小覆盖集 64 int CovSet(int k) 65 { 66 mem(vis,false); 67 int ans=0; 68 //不处理根节点1 69 for(int i=k;i > 1;--i) 70 { 71 int v=vs[i]; 72 int f=fa[v]; 73 if(!vis[v] && !vis[f])//如果当前节点和父亲节点都不属于顶点集覆盖 74 { 75 covSet[f]=true;//将父亲节点加入到覆盖集 76 ans++; 77 vis[v]=true; 78 vis[f]=true; 79 } 80 } 81 return ans; 82 } 83 //求最大独立集 84 int IndSet(int k) 85 { 86 mem(vis,false); 87 int ans=0; 88 for(int i=k;i >= 1;--i) 89 { 90 int v=vs[i]; 91 int f=fa[v]; 92 if(!vis[v])//如果当前节点没有被覆盖 93 { 94 indSet[v]=true; 95 ans++; 96 vis[f]=true; 97 vis[v]=true; 98 } 99 } 100 return ans; 101 } 102 void Solve() 103 { 104 //以任意节点当根节点都可以 105 int k=0; 106 Dfs(1,1,k); 107 int ans1=DomSet(k); 108 int ans2=CovSet(k); 109 int ans3=IndSet(k); 110 printf("The total point of minimum dominate set is %d\n",ans1); 111 printf("The total point of minimum cover set is %d\n",ans2); 112 printf("The total point of maximum independent set is %d\n",ans3); 113 } 114 void Init() 115 { 116 num=0; 117 mem(head,-1); 118 mem(domSet,false); 119 mem(covSet,false); 120 mem(indSet,false); 121 } 122 int main() 123 { 124 while(~scanf("%d",&n)) 125 { 126 Init(); 127 for(int i=1;i < n;++i) 128 { 129 int u,v; 130 scanf("%d%d",&u,&v); 131 addEdge(u,v); 132 addEdge(v,u); 133 } 134 Solve(); 135 } 136 return 0; 137 } 138 /** 139 11 140 1 3 141 3 11 142 11 10 143 11 9 144 1 4 145 4 2 146 2 8 147 4 7 148 7 5 149 7 6 150 */
相关习题:




