线段树区间合并
https://vjudge.net/problem/HDU-3308
•参考资料
[1]:ACM线段树的区间合并(图文) [提取码:o380]
[2]:博客
[3]:线段树总结
•抛出问题
- 给出一个序列,仅由 0 和 1 组成
- 给出一个区间 [ l , r ]
- 求这个区间中只包含 1 的子串的最大长度
•歪门邪道
- 区间 DP : 时间复杂度 O(n3) 的预处理,O(n) 的询问
- 胡乱预处理+询问O(n2)
•但是如果增加新的条件呢?
- 给出a,b,要求将第a位的值改为b
- 刚才给出的解法都是依靠预处理来达到之后的询问时间的
- 如果我们要做修改操作,就要重新预处理
•联想线段树的作用
- 如果我们能够使用线段树来解决这类区间查询问题(但并不是简单的带修改求和或RMQ)
- 我们可以达到修改的 O(logn) 和查询的 O(logn)
- 线段树的建造是 O(nlogn),查询的总时间就是O(nlogn)
- 即使不带修改也要比前面的方法优秀
•解决这类问题,线段树由固定的套路
- 这类问题基本是 “带修改的区间查询”,“连续” 问题
- 他可以问你一个区间的 LCIS 或者是一个区间的连续某数字等等
•正解
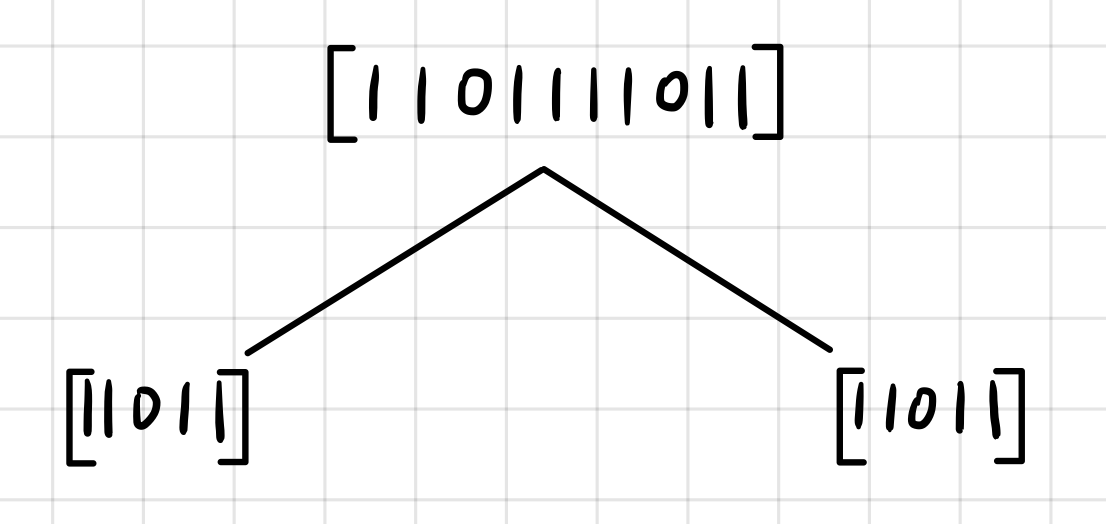
如图所示,是由"1101111011" 构造的一颗线段树,要求某区间连续的 1 的个数(一部分,都画出来太麻烦了,主要是用于方便理解概念用的)
在此之前,先声明一下我的代码风格:
1 #define ls(x) (x<<1)//左儿子 2 #define rs(x) (x<<1|1)//右儿子 3 4 struct Seg 5 { 6 int l,r; 7 int lsum,rsum; 8 int sum; 9 int mark;//懒惰标记 10 int mid(){ return l+((r-l)>>1);} 11 int len(){ return r-l+1;} 12 }seg[maxn<<2];①首先介绍一下相关概念
lsum : 从本节点区间最左端开始(向右)一共有 lsum 个连续的1;(seg[1].lsum = 2)
rsum : 从本节点区间最右端开始(向左)一共有 rsum 个连续的1;(seg[1].rsum = 2)
sum : 本区间一共最多有 sum 个连续的1;(seg[1].sum = 4)
mark : 区间更新的懒惰标记,比如,如果将区间 [l,r] 中所有的1变为0,那么 mark = 0 就意味着要将此区间中的所有1变为0;
②如何求解 lsum,rsum,sum ? 下面介绍函数pushUp(int pos)的作用
pushUp(int pos) : 把当前pos结点的"左右儿子的节点"信息更新到pos结点;
例如,假设求出 1号 节点 "1101111011" 的左右儿子节点的 lsum,rsum,sum,那么便可通过 pushUp(1) 来求出 1号节点的lsum,rsum,sum值;
seg[1].lsum = seg[ls(1)].lsum;
seg[1].rsum = seg[rs(1)].rsum;
这两个操作是毋庸置疑的,1号节点的 lsum 至少为 ls(1) 号节点的 lsum,但有没有可能比 seg[ls(1)].lsum 大呢?
答案是肯定的,如果 seg[ls(1)].lsum = segTree[ls(1)].len(),那么
seg[1].lsum = seg[ls(1)].lsum + seg[rs(1)].lsum;
如上图,如果将1号节点的左儿子中的'0'改为'1',那么seg[1].lsum = 5+2 = 7;
seg[1].rsum 同理;
那seg[1].sum 该如何求呢?
很显然,它等于 (左儿子的sum值,右儿子的sum值,左儿子的rsum+右儿子的lsum值)三者的最大值;
pushUp()函数代码如下:
1 //返回三者最大值 2 int Max(int a,int b,int c) 3 { 4 return max(max(a,b),c); 5 } 6 void pushUp(int pos) 7 { 8 seg[pos].lsum=seg[ls(pos)].lsum; 9 seg[pos].rsum=seg[rs(pos)].rsum; 10 11 //判断是否可以增加 12 if(seg[pos].lsum == seg[ls(pos)].len()) 13 seg[pos].lsum += seg[rs(pos)].lsum; 14 if(seg[pos].rsum == seg[rs(pos)].len()) 15 seg[pos].rsum += seg[ls(pos)].rsum; 16 17 seg[pos].sum=Max(seg[ls(pos)].sum, 18 seg[rs(pos)].sum, 19 seg[ls(pos)].rsum+seg[rs(pos)].lsum); 20 }③介绍完 pushUp(int pos) 函数后,下面来介绍 pushDown(int pos) 函数的作用
pushDown(int pos) : 把当前pos结点的信息传递给儿子结点;
还记得区间更新懒惰标记中的 pushDown(int pos) 函数吗?
之所以能够正确求解,就是这个函数的作用;
在区间更新,查询操作中,每来到一个大区间,都要将这个区间的懒惰标记向下传递,这样才不会出错。
那么线段树区间合并中的 pushDown(int pos) 的作用也差不多;
假设有两种操作:
1.将区间 [l,r] 全变为'0';
2.将区间 [l,r] 全变为'1';
那么,相应的,mark就需要有三个取值:
mark = -1 : 不做任何操作;
mark = 1 : 将区间[l,r]全变为'1';
mark = 0 : 将区间[l,r]全变为'0';
如果 seg[pos].mark = 1,那么在向下传递标记的时候,左右儿子的 lsum,rsum,sum 分别全都变为 seg[ls(pos)].len() , seg[rs(pos)].len();
如果 seg[pos].mark = 0,那么在向下传递标记的时候,左右儿子的 lsum,rsum,sum 全都变为0
pushDown(int pos)代码如下:
1 void F(int pos,int val) 2 { 3 seg[pos].lsum=val; 4 seg[pos].rsum=val; 5 seg[pos].sum=val; 6 } 7 /** 8 mark=-1 : no operator 9 mark= 1 : 0变成1 10 mark= 0 : 1变成0 11 */ 12 void pushDown(int pos) 13 { 14 int &mark=seg[pos].mark; 15 if(mark == -1) 16 return ; 17 seg[ls(pos)].mark=mark; 18 seg[rs(pos)].mark=mark; 19 if(mark == 0) 20 { 21 F(ls(pos),0); 22 F(rs(pos),0); 23 } 24 else 25 { 26 F(ls(pos),seg[ls(pos)].len()); 27 F(rs(pos),seg[rs(pos)].len()); 28 } 29 mark=-1; 30 }④介绍完主要的pushUp(),pushDown()后,建树,查询,更新操作就比较简单了
POJ3667 "Hotel"(简单的区间和并问题)
•题意
有 n 间房,初始每间房都为空;
m 次操作,每次操作有两种:
(1)1 x : 找连续的 x 间房住人,并要求第一间房的编号尽可能小,找不到输出 0
(2)2 x y : 房间 [x,...,x+y-1] 重置为空房间;
输出操作(1)对应的答案;
•题解
将这 n 个房间看成长度为 n 的串,0 表示房间为空,1 表示房间住人;
那么,根据题目要求,就是求连续的 0 的个数,满足至少有 x 个连续的 0,并且起始位置编号最小;
根据上面对线段树区间更新的分析,首先,我定义如下数据结构:
1 struct Seg 2 { 3 int l,r; 4 /** 5 lsum:[l,...,r]从左开始数连续的0的个数; 6 rsum:[l,...,r]从右开始数连续的0的个数; 7 sum:[l,...,r]连续的0的最大值; 8 */ 9 int lsum,rsum,sum; 10 int lazy;///-1:无操作; 0:[l,...,r]房间置空;1:[l,...,r]房间住人 11 int mid(){return l+((r-l)>>1);} 12 int len(){return r-l+1;} 13 }seg[maxn<<2];对于询问操作,根据题目要求,优先递归左儿子;
如果左儿子没有那么多连续的空房间,优先判断左儿子的 rsum 与右儿子的 lsum 是否有 x 个连续的空房间;
如果有,直接输出 seg[ls(pos)].r+1-seg[ls(pos)].rsum;
最后,如果上述两种方案都不行,递归右儿子;
•Code