KMP && KMP求字符串循环节

 

•参考资料

　　[1]:KMP学习资料：左神进阶班第一节 

 

KMP学习小结

•KMP的用途

　　对于给定的两个串 S,T，如何在线性时间内判断 S 是否包含 T 呢？

　　以下默认 S,T 下标从 0 开始；

•前置知识

　　$next$ 数组，定义 $next_i$ 表示 T 中前 i 个字符 （$T_0,T_1,\cdots ,T_{i-1}$） 最长前缀和最长后缀的匹配长度并且满足 $next_i < i$；

　　并人为规定 $next_0=-1,next_1=0$；

　　例如，假设 $T="aaaab"$，$next$ 求解情况如下：

　　　　$\begin{aligned} next_0 &= -1 \\ next_1 &= 0 \\next_2 &=1\ (prefix="a",suffix="a") \\ next_3&=2\ (prefix="aa",suffix="aa")\\ next_4&=3\ (prefix="aaa",suffix="aaa") \\ next_5&=0\ (don't\ exsits\ prefix = suffix)\end{aligned}$;

　　$next$ 数组的求解可以通过动态规划在线性时间内完成；

int next[maxn];
void getNext(const char *s)
{
    int len=strlen(s);
    next[0]=-1;
    next[1]=0;
    int index=2;
    int cnt=0;
    while(index <= len)
    {
        if(s[index-1] == s[cnt])
            next[index++]=++cnt;
        else if(cnt != 0)
            cnt=next[cnt];
        else
            next[index++]=0;
    }
}

•通过KMP判断S是否包含T

　　

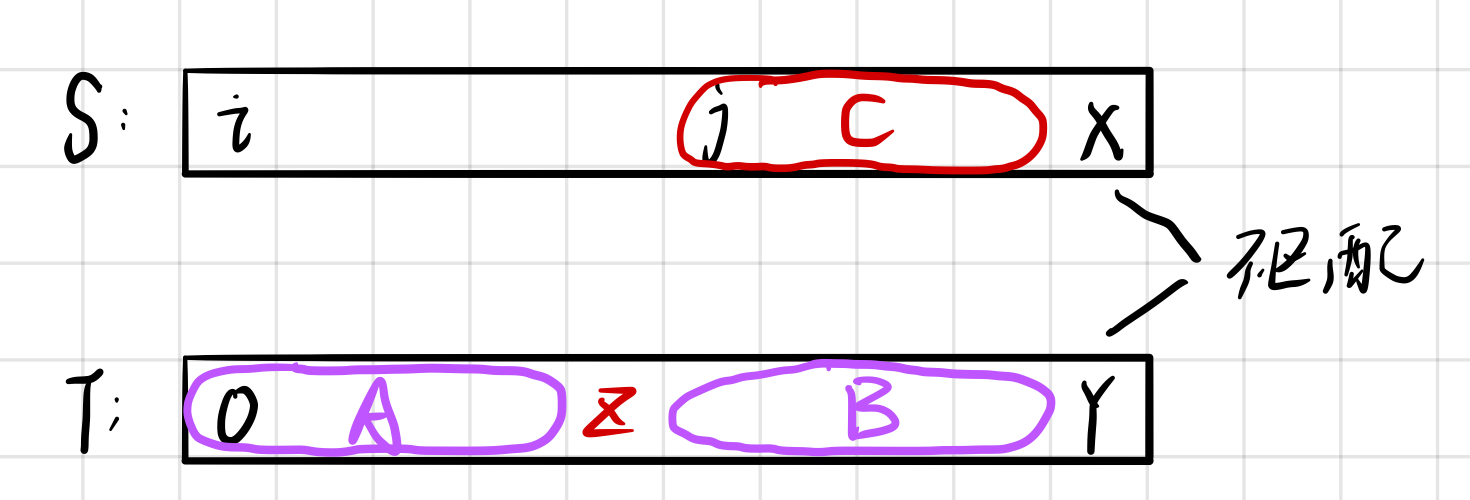
　　假设当前是从 S 的 i 位置匹配 T 的 0 位置，并且 $S[x] \neq T[y]$；

　　A,B 是通过 $next_y$ 求出的最长前缀和最长后缀的匹配串；

　　易得 C=A=B，那么，当前位置失配后，下一个匹配的位置为 S[x] 与 T[z] ；

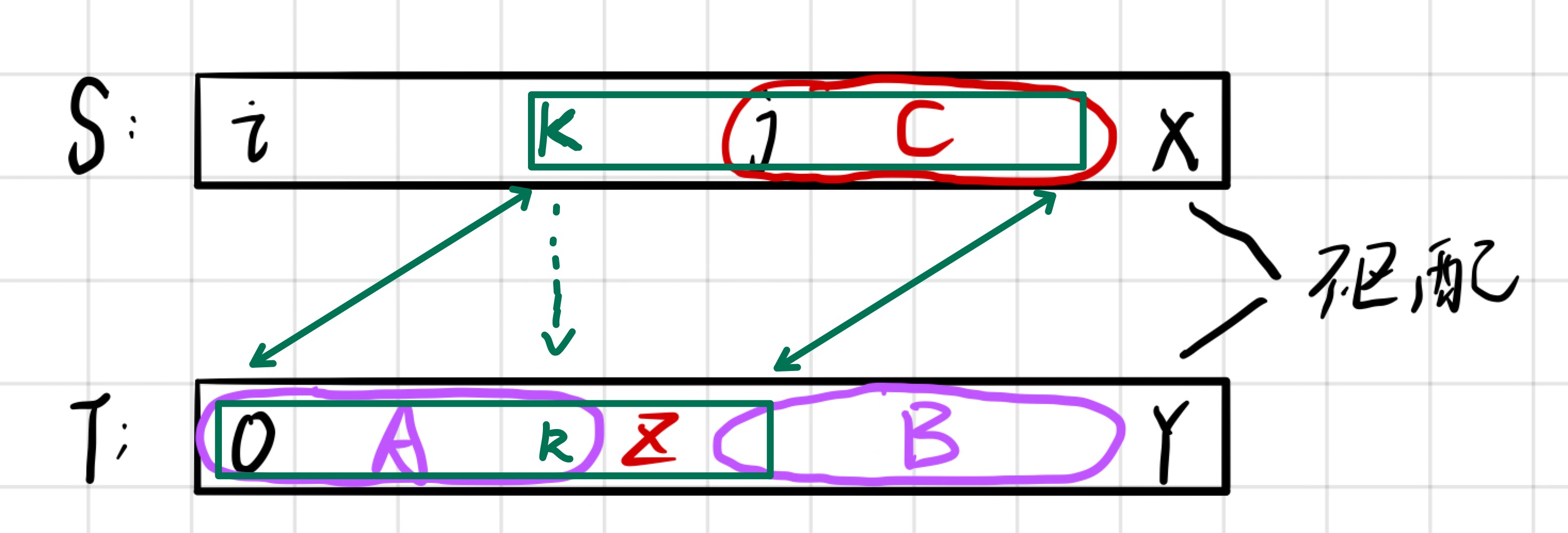
　　并且很容易证明 $[i+1,j-1]$ 中，以任意下标为开始都不会完整的匹配出 T；

　　用 $next$ 数组证明如下：

　　　　假设 $[i+1,j-1]$ 中存在一位置 K，从 K 位置出发可以匹配出 T;

　　　　

　　　　那么就有 S[K,......,X-1] = T[0,......,X-1-K](图中的绿色方框);

　　　　又因为 S[K,......,X-1] = T[k,......,Y-1]，那么 T[0,......,X-1-K] = T[k,......,Y-1]；

　　　　也就是说，Y 之前找到了比 next[Y] 更长的一对相等的最长前缀和最长后缀；

　　　　但是因为 next 数组求解的是正确的，所以，就不会存在 K 位置，使得 S 从 K 位置出发可以匹配出 T。

　　　　证毕。

struct KMP
{
    int next[maxn];
    void getNext(const char *s)
    {
        int len=strlen(s);
        next[0]=-1;
        next[1]=0;
        int index=2;
        int cnt=0;
        while(index <= len)
        {
            if(s[index-1] == s[cnt])
                next[index++]=++cnt;
            else if(cnt != 0)
                cnt=next[cnt];
            else
                next[index++]=0;
        }
    }
    bool kmp(const char *s,const char *t)///判断串s是否包含串t
    {
        getNext(t);
        int n=strlen(s);
        int m=strlen(t);
        int x=0;///s的下标索引
        int y=0;///t的下标索引
        while(x < n && y < m)
        {
            if(s[x] == t[y])///s[x]匹配t[y],都++去匹配下一个位置
                x++,y++;
            else if(y == 0)///如果y==0,只能让x来到下一个位置
                x++;
            else///通过next数组找需要x匹配的位置
                y=next[y];
        }
        ///如果y == m，说明在串S包含串T
        return y == m ? true:false;
    }
}_kmp;

应用1-2019ICPC徐州网络赛D.Carneginon

•题意

　　给你一个 串T 和 q 次询问，每次询问给出一个 串S；

　　对于每次询问，判断 T 和 S 的包含关系；

　　（1）如果 |T| > |S|

　　　　T 包含 S，输出 "my child!";

　　　　反之，输出 "oh, child!";

　　（2）如果 |T| < |S|

　　　　S 包含 T，输出 "my teacher!";

　　　　反之，输出 "senior!";

　　（3）|T| = |S|

　　　　如果 T = S，输出 "jntm!";

　　　　反之，输出 "friend!";

　　并且，题目给出的数据范围 $q\times (|S|+|T|)\leq 10^7$，所以每次判断跑一遍 KMP 是完全可以 AC 这道题的；

•Code

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+50;

char s[maxn];
char t[maxn];
struct KMP
{
    int next[maxn];
    void getNext(const char *s)
    {
        int len=strlen(s);
        next[0]=-1;
        next[1]=0;
        int index=2;
        int cnt=0;
        while(index <= len)
        {
            if(s[index-1] == s[cnt])
                next[index++]=++cnt;
            else if(cnt != 0)
                cnt=next[cnt];
            else
                next[index++]=0;
        }
    }
    bool kmp(const char *s,const char *t)///判断串s是否包含串t
    {
        getNext(t);
        int n=strlen(s);
        int m=strlen(t);
        int x=0;///s的下标索引
        int y=0;///t的下标索引
        while(x < n && y < m)
        {
            if(s[x] == t[y])///s[x]匹配t[y],都++去匹配下一个位置
                x++,y++;
            else if(y == 0)///如果y==0,只能让x来到下一个位置
                x++;
            else///通过next数组找需要x匹配的位置
                y=next[y];
        }
        ///如果y == m，说明在串S包含串T
        return y == m ? true:false;
    }
}_kmp;

int main()
{
    scanf("%s",t);

    int q;
    scanf("%d",&q);
    while(q--)
    {
        scanf("%s",s);

        int n=strlen(t);
        int m=strlen(s);

        if(n > m)
        {
            if(_kmp.kmp(t,s))
                puts("my child!");
            else
                puts("oh, child!");
        }
        else if(n < m)
        {
            if(_kmp.kmp(s,t))
                puts("my teacher!");
            else
                puts("senior!");
        }
        else if(_kmp.kmp(s,t))
            puts("jntm!");
        else
            puts("friend!");
    }
}

 

 

---

 

对KMP求字符串循环节的理解

•前置知识

　　KMP中的 next 数组；

•结论

　　长度为 len 的字符串, 如果 $(len-next_{len})\ |\ len$ ，则循环次数为 $\frac{len}{len-next_{len}}$，否则为1。

•证明

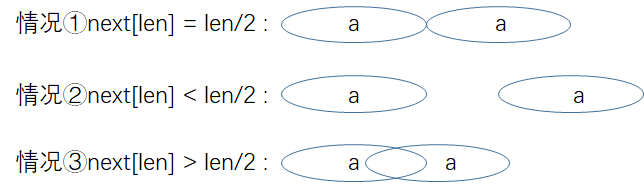
　　分三种情况讨论：

　　　　

　　情况①：显然  len-next[len] | len , 循环次数为 2

　　情况②：len-next[len] 一定不整除 len，证明如下：

　　　　假设 s串 由若干个 a 串和 b 串组成，为方便表述，就固定有4个a串和1个b串，且假设|a| = a , |b| = b：

　　　　

　　　　假设 len-next[len] | len , 即 2a+b | 4a+b;

　　　　由带余除法可得 b = ka+r; ( 0 <= r < a)
　　　　那么 2a+b | 4a+b ⇔ (2+k)a+r | (4+k)a+r;
　　　　相当于 [(4+k)a+r] % [(2+k)a+r] = 0;
　　　　下面我们来化简这个式子：
　　　　[(4+k)a+r] % [(2+k)a+r] = [(2+k)a+r+2a] % [(2+k)a+r] = 2a%[(2+k)a+r];
　　　　易得 (2+k)a+r > 2a;(k和r不会同时为0,除非 b = 0,这就与题设不符了)
　　　　所以 2a % [(2+k)a+r] = 2a ≠0;
　　　　所以假设不成立；
　　　　证毕；

　　情况③：（证明待给出）

　　　　(3.1)假设 s串 由长度为 a 的串循环 k 次构成：

　　　　

　　　　len = k×a , next[ len ] = (k-1)×a;

　　　　len - next[len] = a , len / (len - next[len] = k;

　　　　所以可得循环次数为 k;

　　　　(3.2)

　　　　.......................... 

应用

•题目描述

　　给出一字符串 s，求出最少需要增加多少字符使得字符串 s 变成循环次数 ≥ 2 的串？

•解析

　　1.如果 len%(len-nex[len]) == 0 && nex[len] != 0 ，答案为 0;

　　2.如果 $next_{len} < \frac{len}{2} $，答案为 $len-2\times next_{len}$;

　　3.如果 $next_{len} \geq \frac{len}{2} $，设 k = len-next[len]，那么答案为 k-len%k;

　　情况1显而易见；

　　情况2对应的字符串如下图所示：

　　　　

　　字符串s的最长公共前缀与最长公共后缀不重合，那么最少需要增加 |b| 个字符，形成 abab 类型的循环串；

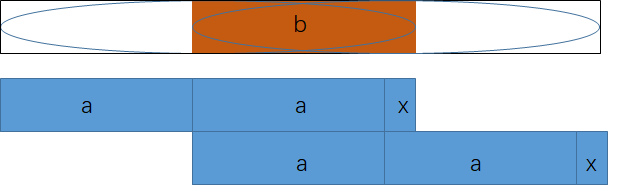
　　情况3对应的字符串如下图所示：

　　　　

　　字符串s的最长公共前缀与最长公共后缀重合，重合长度为 |b|；

　　那么只需在末尾补充字符 $s_x,s_{x+1},\cdots ,s_{a-1}$ 即可和 串x 一起形成 串a；

　　这样的话，串S 就变成了由  串a 循环四次构成的串；

　　此时最少需要增加 |a|-|x| 个字符；

　　|b| = 2×next[len] - len;

　　|a| = next[len] - |b| = len-next[len] = k;

　　|x| = len%a;

　　|a| - |x| = |a| - len%|a| = k - len%k;