群和Pólya定理基础知识
1.1群与置换群
1.1.1群的定义：
给定一个集合G={a,b,c,.......}，和集合G上的二元运算 * ，如果满足以下条件：
(1)封闭性：对于任意a,b ∈ G，a*b ∈ G 成立。
(2)结合律：对于任意a,b,c ∈ G，a*(b*c) = (a*b)*c 成立。
(3)存在单位元素：在G中存在一个元素 e，使得对于任意 a ∈ G，恒有 a*e = e*a = a，元素 e 称为单位元素。
(4)存在逆元：对于G中的任意元素 a，恒有一个 b ∈ G，使得 a*b = b*a = e。元素 b 称为是元素 a 的逆元素，记为 a-1。
则称集合G在运算 * 下是一个群，记作（G，*）。
若G是一个有限集，则称（G，*）为有限群，其中有限群G的元素个数叫做群的阶，记作|G|。
G中的元素 a 和 b 的运算 a*b 可以简记为 ab。
（PS : * 是定义在G上的二元运算，不仅仅局限于 +,-,×,÷,还包含一些其他的二元操作）
例如：
1.1.2子群的定义：
设G是群，H是G的子集，若H在G原有的运算下也是一个群，则称H为G的一个子群。
1.1.3置换的定义：
置换实际上就是排列，n 阶置换共有 n! 个。
我们把{1,2,3,.....,n}的所有 n! 个置换构成的集合记为 Sn 。
1.1.4置换乘法：
一般来说 P1P2 ≠ P2P1。
1.1.5置换群定义：
[1,n]上的由多个置换组成的集合在上面的乘法顶一下构成的一个群称为置换群，记作 Gn 。
置换群满足消去律：
f*g = f*h ，那么 g = h 。
1.1.6恒等置换
恒等置换就是各整数对应到他自身的 {1,2,3,.....,n} 的置换，记作 τ
显然 τ*f = f*τ = f 对 Sn中的所有置换 f 成立。
1.1.7逆函数
由于Sn中的每个置换是一对一函数，所以存在逆函数 f-1 ∈ Sn 满足：
如果 f(s) = k , 那么 f-1(k) = s
通过交换 f 的 2×n 矩阵的第一行与第二行，并重新排列各列使得第一行的整数以自然顺序 1,2,3,.....,n 出现，便得到 f-1 的 2×n 矩阵。
对于每个置换 f，定义 f0 = τ 。
于是恒等置换的逆就是他自身：τ-1 = τ 。
1.2循环与对换
1.2.1循环
可以把m阶循环记为：
定理1.2.2：
任何一个置换都可以表示成若干个互不相交的循环的乘积，且这种表示是唯一的（除了循环的次序可以交换外）。
定理1.2.3：
任意一个循环都可以表示成若干个对换之积。
例如：
(1 2 3 ...... n) = (1 2)(1 3)(1 4)...........(1 n)
= (2 3)(2 4)(2 5)....(2 n)(2 1)
任一置换拆分成若干个置换的乘积，拆分个数的奇偶性是不变的，即要么拆分成偶数个对换之积，要么拆分成奇数个对换之积。
1.2.4：奇对换与偶对换
若一个置换可以拆分成奇数个对换之积，叫做奇置换，反之，叫做偶置换。
奇置换 ≠ 偶置换。
1.3共轭类
1.3.1
为方便理解，先给出{1,2,3,4}置换的全体：
一般可把 Sn中任一置换 P 拆分成若干互不相交的循环乘积：
P = (a1 a2 a3 ..... ak1)(b1 b2 b3 ..... bk2)......(h1 h2 h3 ..... hkm)
其中 k1+k2+.....+km = n 。
设其中 k 阶循环出现的次数为 Ck , k=k1,k2,.....km。
k 阶循环出现 Ck 次用 (k)Ck 表示。
Sn中的置换可按分解成
(1)C1(2)C2 .......... (n)Cn
的不同而分类。其中 Ci = 0 的项 (i)Ci 可以省略(i=1,2,3,....n)。
例如 (1)(2)(3 4)(5 6 7)属于格式
(1)2(2)1 (3)1 。
显然有
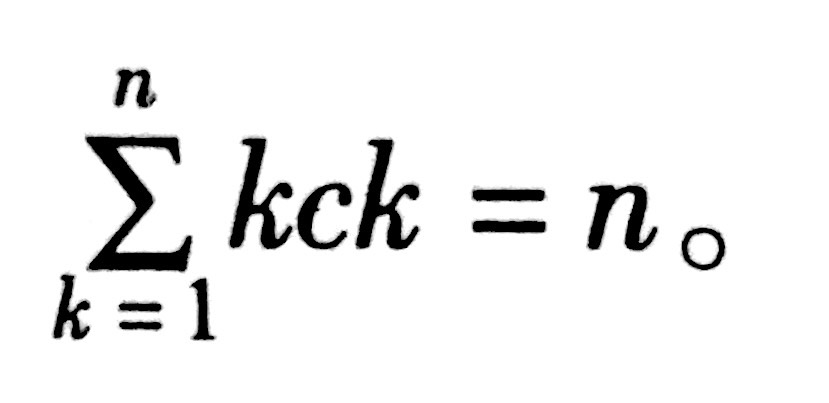
定理1.3.2
1.3.3 k不动置换类和等价类
设 G 是{1,2,3,....n}的置换群，显然 G 是 Sn 的一个子群。
若 k 是 1 到 n 的某个整数，G 中使 k 保持不变的置换全体，记作 Zk ，叫做 G 中使 k 保持不懂得置换类，
或者简称 k 不动置换类。
例如：
G = { e,(1 2),(3 4),(1 2)(3 4) } ，其中 (1 2) = (1 2)(3)(4)，故有
Z1 = { e,(3 4) }
Z2 = { e,(3 4) }
Z3 = { e,(1 2) }
Z4 = { e,(1 2) }
定理1.3.4
G群中关于 k 的不动置换类 Zk 是 G 的一个子群。
