【深度学习入门向】使用几个技巧提高对 CIFAR10 分类的准确性

Mixup, TTA, and Ensemble

在上一篇文章中使用了普通的 CNN 实现了对 CIFAR10 数据集 89% 的准确率。

本文通过实现三种技术来进一步提高准确率

• Mixup：训练时，将两张图像按照一定比例混合合成为新的图像作为训练数据；
• TTA：测试时，将测试集数据经过和训练集数据相同的数据增强后再进行测试；
• Ensemble：融合多个模型以达到更好的效果。

你可以在这里找到本文的具体实现。

Mixup

论文地址 Mixup

训练时将两张原图和对应标签（的 one-hot 编码）按照一定比例混合后再传入网络，可以减小网络在不同样本中的震荡。比如现在有两种图像及其对应标签 \((X_i,y_i),(X_j,y_j)\)，将标签的 one-hot 编码记为 \(p_i,p_j\)

\[\begin{align*} X_{\rm mixup}&=\lambda X_i+(1+\lambda)X_j,\\ p_{\rm mixup}&=\lambda p_i+(1+\lambda)p_j.\\ \end{align*} \]

其中，比例 \(\lambda\in[0,1]\)，按照经验 \(\lambda\) 一般服从 Beta 分布 \(\lambda\sim\text{Beta}(\alpha=\beta=0.2)\)。使用较低的 \(\alpha,\beta\) 使 \(\lambda\) 更接近 0 或 1。可以将 \(\lambda,1-\lambda\) 中接近 1 的一项看作原图，接近 0 的一项看作扰动，如果 \(\lambda\) 太接近 0.5 可能使新数据太过远离原数据。

一种理解 Mixup 的方法是：混合图像其实也是一种数据增强的方式，因为数据增强本质上来说是拓展了原始数据，不再将原始数据看作一个孤立点，而是赋予其周围的数据相同或相似的标签，和原始数据在特征空间组合成一个集合。

一般的方法包括轻微的旋转、平移、翻转、高斯噪声，Mixup 也是如此，不过它的方法是将两个数据用一条线连接起来，并将这条线上的每个点作为新的数据，同时也将标签进行了软化。

当然，和其他数据增强方法一样，增强后的的数据也应当是有意义的，比如水平翻转这种方法在 MNIST 数据集上的部分数据就是无效的。有些数据经过 Mixup 融合反而产生了新的问题，那方法就可能不适用了。

Beta 分布

概率分布函数

\[\begin{align*} f(x)&=\begin{cases} {\Gamma(\alpha+\beta)\over\Gamma(\alpha)\Gamma(\beta)}x^{\alpha-1}(1-x)^{\beta-1}&0\le x\le1\\ 0&\text{else} \end{cases} \end{align*} \]

其中 \(\Gamma\) 函数项是一个为了使分布函数有效的放缩系数，因为

\[\begin{align*} \int_0^1x^{\alpha-1}(1-x)^{\beta-1}\,\mathrm dx&={\Gamma(\alpha)\Gamma(\beta)\over\Gamma(\alpha+\beta)}. \end{align*} \]

从公式的核心 \(x^{\alpha-1}(1-x)^{\beta-1}\) 可以看出其物理意义：事件以概率 \(x\) 成功 \(\alpha-1\) 次，失败 \(\beta-1\) 次的概率。

假设手上有一枚不均匀的硬币，经过 \(n\) 次抛硬币（伯努利试验）后，得到 \(k\) 个正面和 \(n-k\) 个反面。此时通过 Beta 分布，取 \(\alpha=k+1,\beta=n-k+1\)，可以得到最大似然估计下最优的后验概率 \(\arg\max f(x)\)。

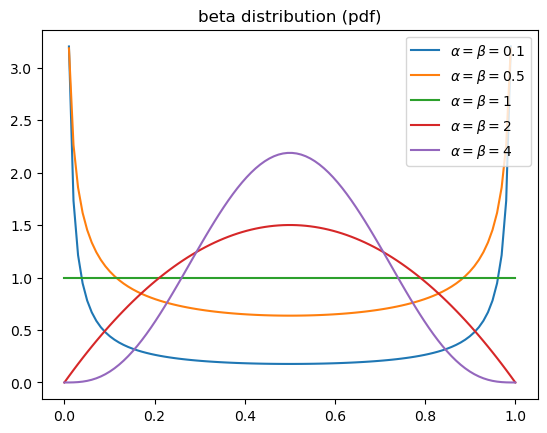
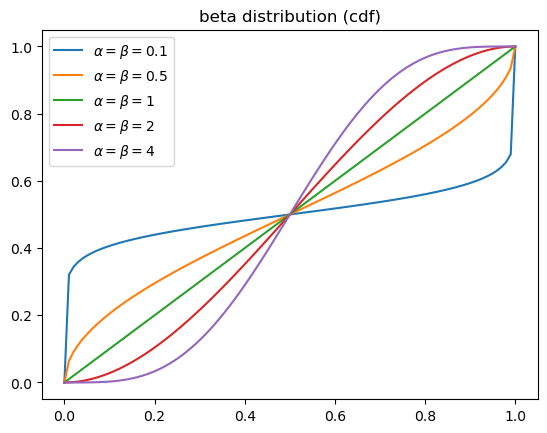
如果 \(\alpha=\beta\)，则概率分布函数关于 \(x=1/2\) 对称；如果选择较小的 \(\alpha,\beta\)，则 \(\text{Beta}(\alpha,\beta)\) 的取值接近于 0 或 1；当 \(\alpha=\beta=1\) 时，变为均匀分布。

TTA

论文地址，TTA

推断时将原图经过数据增强（data augmentation）后再传入网络，得到的结果在进行融合获得最终结果。可以有效的提高准确率。

其大致流程如图所示。

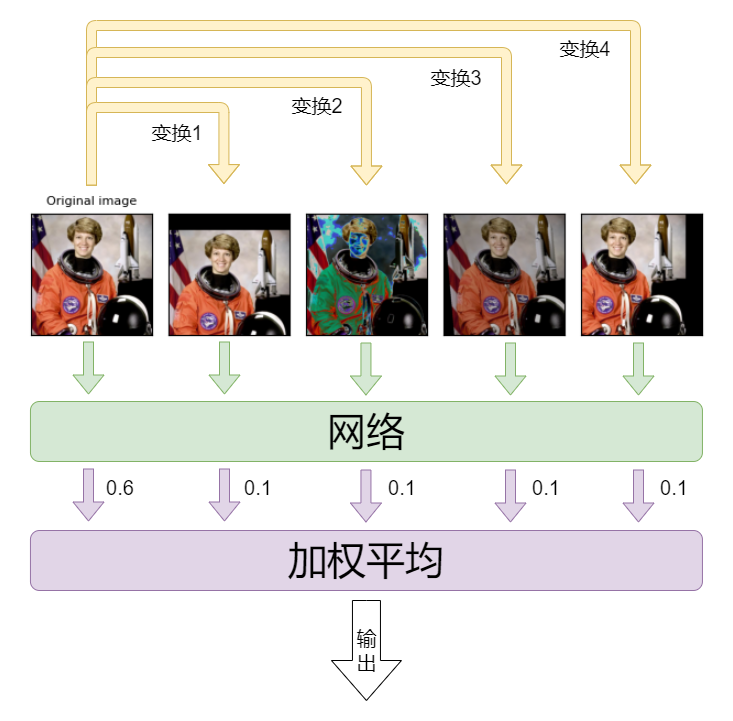
从图中可以看出，由于推断时网络参数是固定的，因此影响 TTA 结果的超参数为变换的选择和结果的权重。

• 变换：不用说也知道应当选择和训练时相近的变换。

• 权重：既可以直接指定，一般将原图的权重设置的比较高；也可以尝试训练这组权重。

  假设经过 \(M\) 个变换后的图像经过网络，得到一个 \(M\times C\) 的矩阵代表不同变换和不同类别的置信度。然后，选择一个合适的聚合函数 \(g:\mathbb R^{M\times C}\to\mathbb R^C\) 将不同变换得出的结果融合。

  比如，加权平均所代表的聚合函数为 \(g(Z;\pmb\theta)=Z^\top\pmb\theta\)。如果有一定数量的训练集，则可以像训练神经网络一样，使用梯度下降法得到一个较优的 \(\pmb\theta\)，其中损失函数同样使用交叉熵损失 \(\mathcal L_{\rm CE}(g(Z;\pmb\theta),y)\)。

Ensemble

Ensemble 和 TTA 在概念上有相似之处，不过此时不是多个变换，而是将多个模型融合在一起。

同样寻找一个合适的聚合函数将多个模型的结果融合在一起，比如少数服从多数的投票法或者简单的加权平均。

本文从简，将本次训练得到的模型和上一次训练的模型进行加权平均来获得最终的预测结果。

结果

model	30 epoch loss	30 epoch accuracy(%)	160 epoch loss	160 epoch accuracy(%)
Shallow-CNN	0.6558	87.09	0.5982	89.63
Mixup-TTA-CNN	0.6434	87.81	0.5528	91.05
Ensemble	0.6209	88.63	0.5617	90.83

其中 Shallow-CNN 代表上一篇文章的结果，Mixup-TTA-CNN 代表本文使用了 Mixup 和 TTA 技术训练新模型，Ensemble 是将这两个模型融合后的结果。可以看到其中最优准确率为 \(91.05%\)。

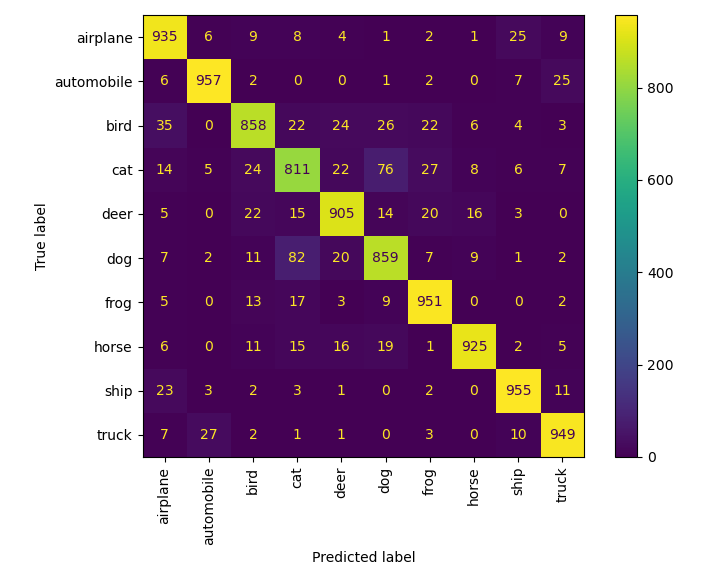
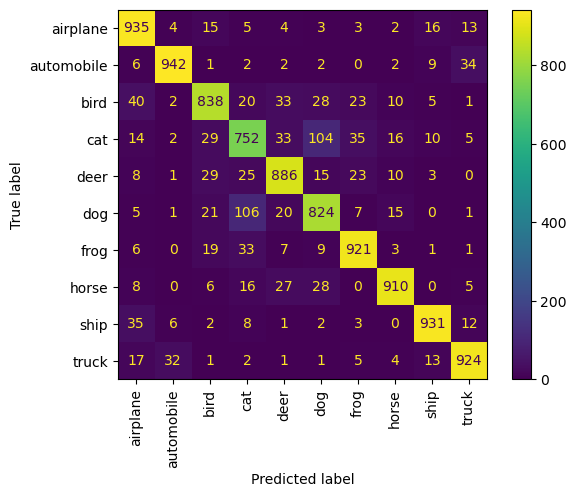
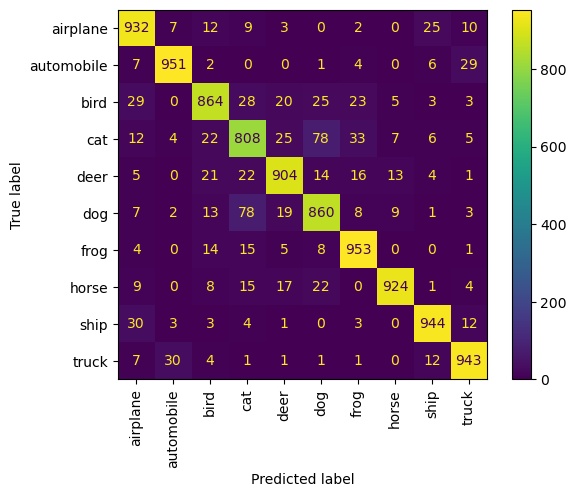
可视化

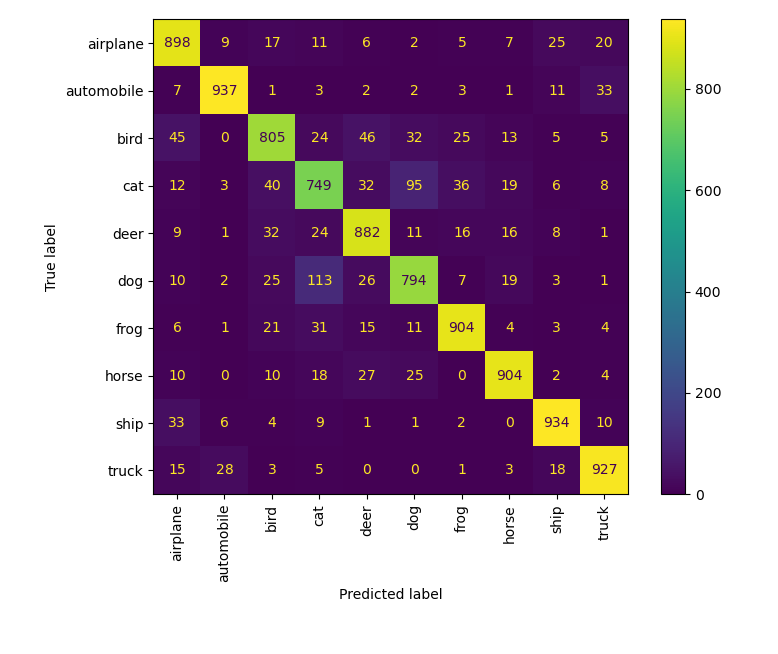
只做了混淆矩阵，从上至下，分别为

• 30 epoch Mixup-TTA-CNN
• 160 epoch Mixup-TTA-CNN
• 30 epoch Ensemble
• 160 epoch Ensemble