使用 CNN 提取内容和风格进行风格迁移（PyTorch 实现）

使用 CNN 提取内容和风格进行迁移

目录

• 使用 CNN 提取内容和风格进行迁移
  • 论文概述
    • 论文地址
    • 基本概念及对应用符号
  • 生成过程
    • 准备
    • 目标
    • 生成
  • 代码实现
    • 网络结构
    • 具体实现
  • 结果

本文演示了使用 CNN 进行风格迁移（style transfer）的深度学习 PyTorch 实现。

完整实现代码位于 https://github.com/VioleshnvQuetsall/neural-transfer 的 cnn-transfer 目录下。

论文概述

论文地址

arXiv 上的预印本 A Neural Algorithm of Artistic Style，IEEE 计算机视觉和模式识别会议（CVPR）上的会议论文：Image Style Transfer Using Convolutional Neural Networks。这两篇论文内容是一样的，只不过前一篇是发在 arXiv 上抢位置的；后一篇则是在会议上发表给同行的，内容会更加详细清楚。因此只需要看后一篇即可。

基本概念及对应用符号

$$\begin{array}{r}\begin{array}{}{X}_C& \text{内容图像}\\ X_S& \text{风格图像}\\ X_G& \text{生成图像}\\ F_{XL}^n& \text{图像 }X\text{ 的第 }L\text{ 层的第 }n\text{ 个特征图展开成向量}\\ F_{XL}& F_{XL}^n\text{ 组成的矩阵}\\ G_{XL}& F_{XL}\text{ 的 Gram 矩阵}\end{array}\end{array}$$

在论文中，图像分为两个相对独立的部分：风格（style）和内容（content），这两个名称在本文中是专有名词，特指通过卷积神经网络进行提取的图像的两部分。

一张图像可以在网络传播的过程中导致不同卷积核不同程度的响应，也就是和卷积核表示的特征对应上了。而一般来说，越深的卷积层所表示的特征就更加复杂，也代表着更具体的形象。有过神经网络的卷积核可视化经验的人应该会有更深的体会。

卷积核的可视化方式可以简单的通过将一张图片传入神经网络并查看各个卷积核的响应；也可以将一张白噪声图片传入神经网络后，尝试通过修改这个白噪声图片，来最大化你所想要的卷积核的响应，进而将白噪声图片变为卷积核最“感兴趣”的图片。

下第一张图就是我在 Fashion-MNIST 上训练的一个简单 CNN 的第一层卷积核响应，可以看到都是一些普通的纹理特征。有名的 DeepDream 其实也是卷积核响应的结果，如下第二张图为在 ImageNet 上训练的一个大型 CNN 的卷积核响应，此时可以看到一些复杂的图形了。

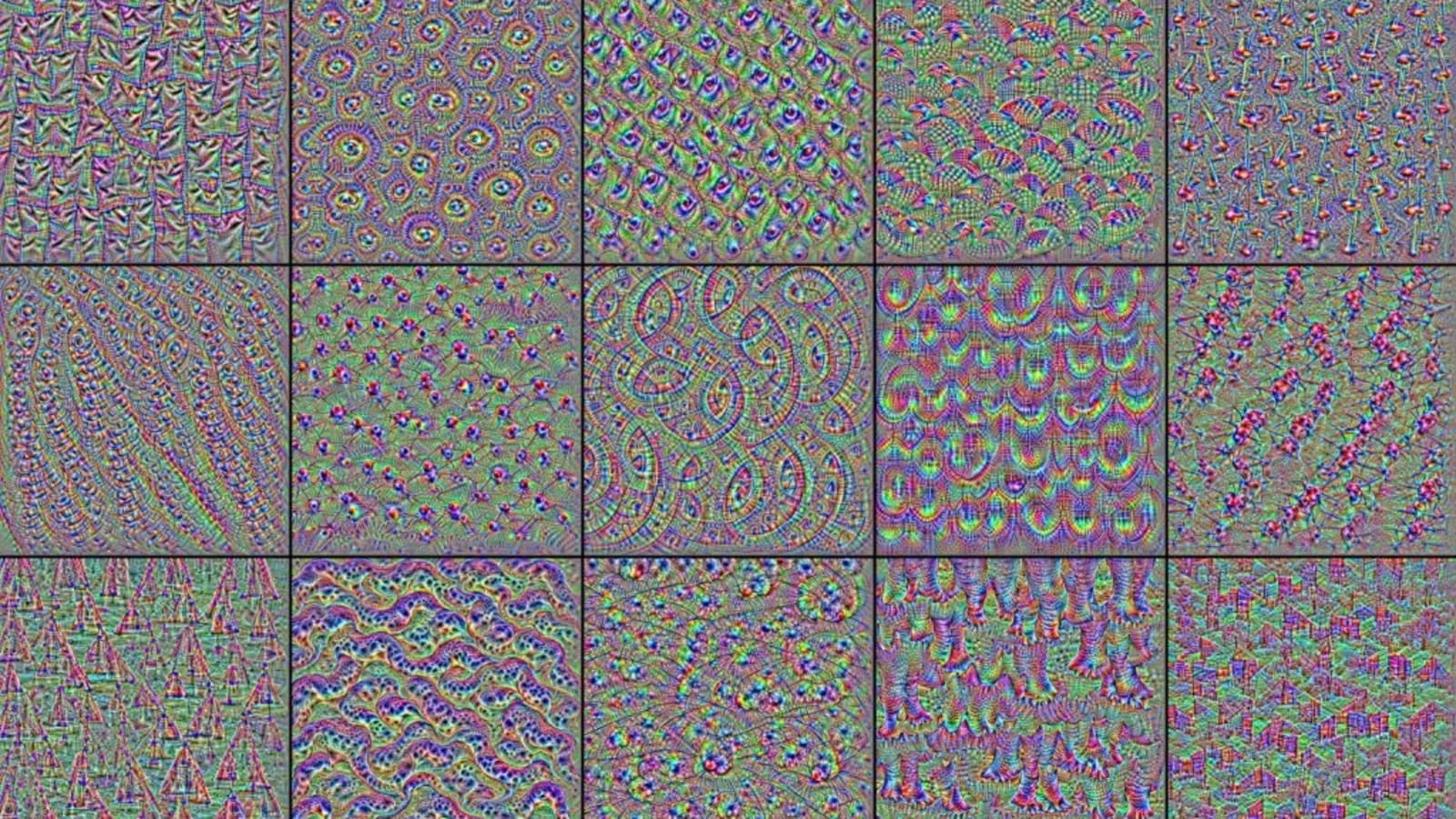
而在这篇论文中，就提出了与后一种方式类似的方法（即最大化卷积核的响应）来进行风格迁移：将内容图片的内容和风格图片的风格通过 CNN 进行分解，然后令图像最大化内容对应的响应和风格对应的响应，将内容和风格组合到一张图片上。

首先论文提出了将一张图像的内容和风格通过 CNN 提取的方法。其中内容为图像在卷积层的响应，而风格为这些响应的 Gram 矩阵。具体来说，一张图像经过神经网络，查看每个卷积层的响应，大小为 $(N,H,W)$，$N$ 为通道数（即这一层的卷积核个数）、卷积结果的高度和宽度。将每个卷积核的响应展开为 $N$ 个 $H\times W$ 维数的向量 $F_{XL}^N$。比如风格图像在 CNN 第 3 层的第 2 个卷积核响应就是 $F{F}_{X_{S}3}^2$。

组合成矩阵 $F_{XL}$，再计算出 Gram 矩阵得到

$$\begin{array}{rl}{F}_{XL}& =\left[\begin{array}{cccc}{F}_{XL}^1& F_{XL}^2& \cdots & F_{XL}^N\end{array}\right]\\ G_{XL,ij}& ={\left[\begin{array}{c}⟨F_{XL}^i,F_{XL}^j⟩\end{array}\right]}_{ij}={\left[F_{XL}^T{F}_{XL}\right]}_{ij}\end{array}$$

其中 $⟨F_{XL}^i,F_{XL}^j⟩$ 表示向量的点积，$G_{XL}$ 的每个元素都是相同或不同卷积核之间的内积。$F_{XL},G_{XL}$ 就是图像 $X$ 在卷积层 $L$ 的内容和风格了，也就是说风格就是同一层卷积核响应的内积。

因为是无监督学习所以不需要标签，直接通过三张图像之间的差异来计算损失。其中生成图像和内容图像的内容损失（Content Loss）、生成图像和风格图像的风格损失（Style Loss）为

$$\begin{array}{rl}{\mathcal{L}}_C:={\mathcal{L}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}}(X_G,X_C,L)& =\frac{1}{2}{\Vert F_{X_{G}L}-F_{X_{C}L}\Vert }_2^2\\ {\mathcal{L}}_S:={\mathcal{L}}_{\mathrm{s}\mathrm{t}\mathrm{y}\mathrm{l}\mathrm{e}}(X_G,X_C,L)& =\frac{1}{4N_L^2{H}_L^2{W}_L^2}{\Vert G_{X_{G}L}-G_{X_{S}L}\Vert }_2^2\end{array}$$

其中 $\Vert FF{\Vert }_2^2$ 为矩阵中每个数的平方和，$\Vert F{\Vert }_2^2=\sum _{i,j}(F_{i,j}{)}^2$。其实很简单，就是图像的内容和风格的均方误差 $MSE$，不过一个不经过放缩（scaling），一个需要放缩。（但是在图像生成的过程中，一般内容图像和风格图像的大小是不变的，等于放缩的比例依然是常数）

虽然现在的框架都支持自动求导了，但我们还是在数学形式上进行一下求导，主要是风格损失的求导计算。

为方便，推导中

$$\begin{array}{r}\begin{array}{}F:=F_{X_{G}L}& F_C:=F_{X_{C}L}\\ G:=G_{X_{G}L}& G_S:=G_{X_{S}L}\\ M:=N_L^2{H}_L^2{W}_L^2\end{array}\end{array}$$

$$\begin{array}{rl}\frac{\partial {\mathcal{L}}_C}{\partial F_{ij}}& =\{\begin{array}{ll}(F-F_C{)}_{ij}& F_{ij}>0\\ 0& F_{ij}<0\end{array}\\ \frac{\partial {\mathcal{L}}_S}{\partial F_{ij}}& =\frac{1}{4M}\frac{\partial }{\partial F_{ij}}\sum _{k,l}{(G-G_S)}_{kl}^2\\ & =\frac{1}{2M}\sum _{k,l}{(G-G_S)}_{kl}\frac{\partial G_{kl}}{\partial F_{ij}}\\ & =\frac{1}{2M}\sum _{k,l}{(G-G_S)}_{kl}\frac{\partial (F^{T}F{)}_{kl}}{\partial F_{ij}}\\ & =\frac{1}{2M}\sum _{k,l}{(G-G_S)}_{kl}({\delta }_{lj}{F}_{ki}^T+{\delta }_{kj}{F}_{il})\\ & =\frac{1}{2M}(\sum _k{(G-G_S)}_{kj}{F}_{ki}^T+\sum _l{(G-G_S)}_{jl}{F}_{il})\\ & =\frac{1}{2M}(\sum _k{(G-G_S)}_{jk}^T{F}_{ki}^T+\sum _l{(G-G_S)}_{jl}{F}_{li}^T)\\ & =\frac{1}{2M}({\left[{(G-G_S)}^T{F}^T\right]}_{ji}+{\left[(G-G_S)F^T\right]}_{ji})\\ & =\frac{1}{M}{\left[F(G-G_S)\right]}_{ij}\\ & =\{\begin{array}{ll}\frac{1}{M}{\left[F(G-G_S)\right]}_{ij}& F_{ij}>0\\ 0& F_{ij}<0\end{array}\end{array}$$

推导过程其中注意 ${\delta }_{ij}=\{\begin{array}{ll}1& i=j\\ 0& i\ne j\end{array}$，$G$ 为对称矩阵。

使用到的矩阵求导公式为

$$\begin{array}{r}\frac{\partial (F^{T}F{)}_{kl}}{\partial F_{ij}}={\delta }_{lj}{F}_{ki}^T+{\delta }_{kj}{F}_{il}\end{array}$$

推导过程可能写得比较繁琐，还请不要在意。值得注意的是 $F_{ij}<0$ 这一项所对应的导数都为 0，这里其实隐藏了一个小细节，其实我们所得卷积层的响应并不是卷积层 Conv2D 的响应，而是连同它后面的激活层一起计算的，而推导的结果其实就是激活层采用 ReLU 的结果，即卷积层的响应指的是 Conv2D+ReLU 的响应（$max(0,x)$）。因此如果 $F_{ij}<0$，那么导数就为 0 了；相对的，如果 $F_{ij}>0$，则导数就等于对 Conv2D 本身求导得到的导数。

我们需要的是生成图像和内容图像、风格图像的差异尽可能小，如果不采用 MSE 作为损失函数也是有可能的。实际上，Gram 矩阵之差的 MSE 等同于使用多项式核函数来衡量其中卷积层响应的差异，因此完全可以使用别的核函数来进行缩小风格损失的计算。

最后，将两个损失结合在一起，因为可以使用很多层，并且可以为每一层赋予不同的权重，所以最终的损失公式是内容损失和风格损失的加权和

$$\begin{array}{r}\mathcal{L}:=\alpha \sum _i{w}_{Ci}{\mathcal{L}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}}(X_G,X_C,i)+\beta \sum _i{w}_{Si}{\mathcal{L}}_{\mathrm{s}\mathrm{t}\mathrm{y}\mathrm{l}\mathrm{e}}(X_G,X_S,i)\end{array}$$

其中 $i$ 就是选择的卷积层，通过调整 $\alpha ,\beta ,ww$ 我们可以获得更接近内容或者更接近风格的图像，并且能够捕捉到不同层次的内容和风格。最终问题变为了最优化问题，可以通过对生成图像进行梯度下降法处理。

生成过程

现在让我们明确一下图像生成的过程

准备

风格图像、内容图像、已经训练好的卷积神经网络（可以提取图像特征图）。

目标

• 提取三幅图片的内容、风格 $F_{XL},G_{XL}$

• 计算损失 $\mathcal{L}=\alpha {\mathcal{L}}_C+\beta {\mathcal{L}}_S$

生成

1. 初始化

   在生成过程中保持三幅（组）图像：风格图像 $X_S$，内容图像 $X_C$，生成图像 $X_G$。其中生成图像 $X_G$ 可以用白噪声、内容图像、风格图像或者任意图像进行初始化。

2. 迭代生成

   1. 将三幅图像传入卷积神经网络获得卷积层响应；

   2. 通过卷积层响应得到内容和风格，计算内容损失和风格损失；

   3. 对生成图像进行梯度下降；

      在一般的深度学习中，是通过对模型的参数进行梯度下降来学习的；但在这里，模型不需要变动，而是对生成的图像进行修改来降低损失。

代码实现

全部代码位于 https://github.com/VioleshnvQuetsall/neural-transfer/tree/main/cnn-transfer

网络结构

具体的卷积神经网络采用 VGG19。我们先来观察一下 VGG 的网络结构，VGG 网络可被分为两个部分：提取特征的卷积池化层和分类的全连接层。从图像的生成过程中可以看到，一些比较深的卷积层可能是用不到的，更不用说全连接层了。已经训练好的 VGG 可以对图像分类，但在风格迁移中不需要分类，只需要使用前面的卷积层来进行特征提取。

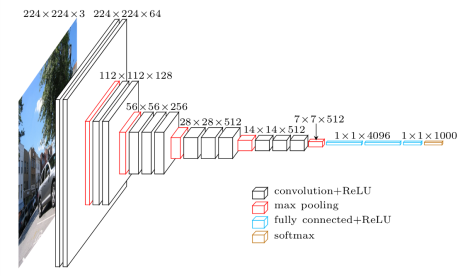
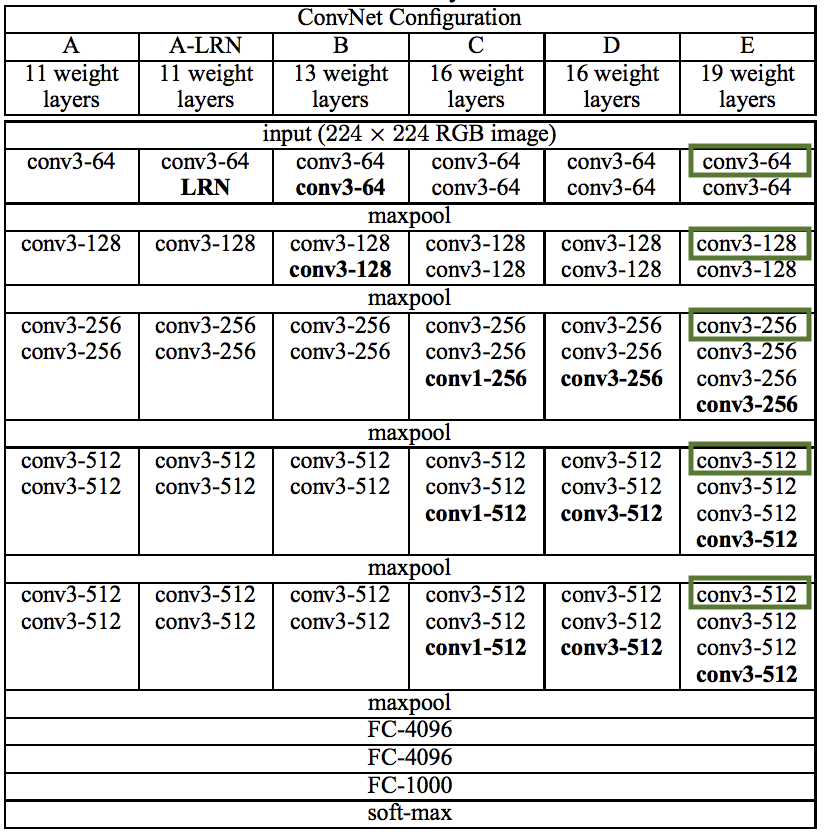
其中 VGG19 具有 16 个卷积层，前两个卷积块有 2 个卷积层，后三个卷积块有 4 个卷积层，将这些卷积层编号为“块-层”。在论文中使用的是 4-2 提取内容图像，1-1、2-1、3-1、4-1 提取风格图像（图片中用绿色框出）。

前文已经提到卷积层的响应实际上指的是 Conv2D+ReLU 的响应，因此尝试在 Conv2D+ReLU 层之后添加损失层。得到如下图所示的网络结构，上面为 VGG19 的特征提取器的结构，在选定的 Conv2D+ReLU 层之后加入损失层得到下图所示的结构。损失层只会计算给定的损失，而不会对网络传输中的响应进行修改。

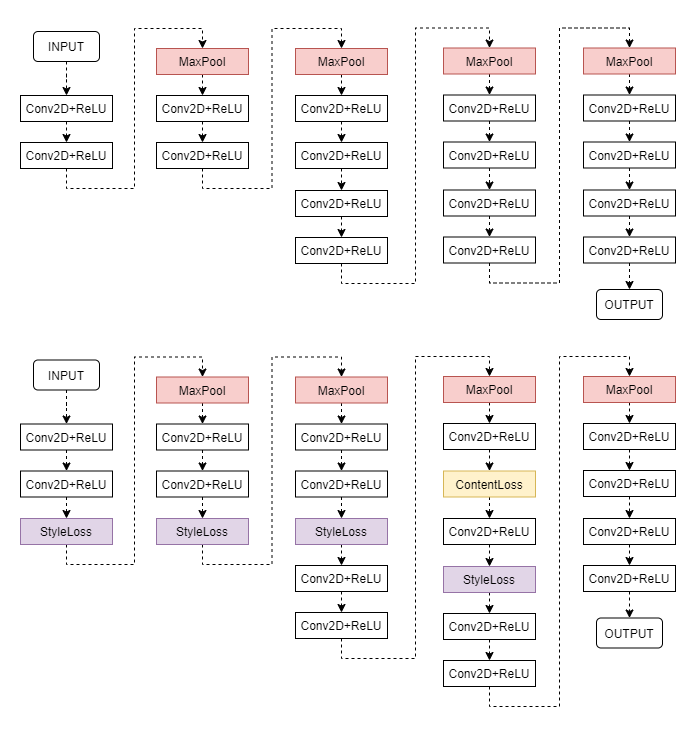
添加完毕后，将内容图像和风格图像分别传入网络对损失层进行初始化。在生成时将生成图像传入网络，令损失层计算损失，之后从这些损失层中提取损失即可。

具体实现

Gram 矩阵的计算，通过神经网络得到的卷积层响应的形状为 $(N,C,H,W)$ 代表着批数量、通道数（卷积核数量）、高度、宽度，变形后得到形状 $(N\times C,H\times W)$ 因此和前面数学公式中 $F_{XL}$ 是转置的关系。得到函数 gram()，可以通过放缩参数来决定是否进行放缩。

def gram(feature_maps, scale=False):
    n, c, h, w = feature_maps.shape
    feature = feature_maps.view(n * c, h * w)
    gram_matrix = torch.mm(feature, feature.t())
    if scale:
        gram_matrix /= n * c * h * w
    return gram_matrix

ContentLoss & StyleLoss

观察两个矩阵的大小，卷积核响应矩阵 $F\in {\mathbb{R}}^{N\times (H\times W)}$，Gram 矩阵 $G\in {\mathbb{R}}^{N\times N}$。可以看到，卷积核响应矩阵的维数和图像的大小有关，而 Gram 矩阵的维数只和卷积核的数量有关。而计算内容损失是通过卷积核响应矩阵，计算风格损失是通过 Gram 矩阵，说明生成图像和内容图像大小要相同，而与风格图像则可以不相同。也就是说在训练过程中可以随意改变风格图像，但内容图像的大小始终要保持一致。

class ContentLoss(nn.Module):
 
    def __init__(self, weight=1):
        super().__init__()
        self.target = None
        self.weight = weight
 
        self.loss_fn = partial(F.mse_loss, reduction='mean')
        self.loss = None
 
        self.load_content = False
        self.activate = False
 
    def forward(self, x):
        if self.activate:
            self.loss = self.weight * self.loss_fn(x, self.target)
        elif self.load_content:
            self.target = x.detach()
        return x

只贴出 ContentLoss 的代码，StyleLoss 是类似的，只不过把 target 改为 Gram 矩阵。

使用 load_content, activate 来控制损失层的行为，到底是是将输入 x 看作是内容图像的响应还是生成图像的响应，也就是作为损失层的初始化还是要计算损失层的损失。

MSE 使用 mean 也就是均值，这一点和数学公式中不一样，不过在实践中发现如果使用 sum 的话损失会过大，因为 sum = N * H * W * mean。不过损失函数也可以换成 scale_mse_loss，这个函数的好处是导数接近常数 1，可以以比较稳定的速率进行优化。

def scale_mse_loss(x, target):
    diff = (x - target)
    return diff.pow(2).sum() / diff.abs().sum().add(1e-8)

和其他神经网络的训练不同，其他神经网络是训练网络，而这里则是训练生成图像，因此要保持网络的参数不变而在生成图像上进行梯度下降。因为要优化的参数量仅为一个图片的大小，相比于一整个网络上百万的参数量来说已经是非常小的了，所以我们可以使用二阶优化器 LBFGS 来优化生成图像。二级优化器比一阶优化器收敛速度更快，但是需要的计算量和容量也更大。

model.requires_grad_(False)
generate_img = torch.randn(content_img.shape, requires_grad=True)
optimizer = torch.optim.LBFGS([generate_img], lr=lr, max_iter=max_iter)

因为 LBFGS 优化器可能在一次优化中进行多次损失计算，这个多次的次数上限由参数 max_iter 决定，所以在优化器优化时传入闭包函数 closure，在闭包函数里面进行真正的正向传播和反向传播来计算损失，再让优化器调用这个函数。

def closure():
    optimizer.zero_grad()
    model(generate_img)
 
    content_loss = sum(lc.loss for lc in content_losses)
    style_loss = sum(ls.loss for ls in style_losses)
 
    loss = alpha * content_loss + beta * style_loss
    loss.backward()
 
    return loss
 
optimizer.step(closure)

结果

在正式开始训练之前，可以将 $\alpha ,\beta$ 分别置零，并使用白噪声来初始化，来观察生成图像对于内容和风格的还原程度。比如下图就是使用了 4-2 层来复原内容图像的结果，实际上在 100 epochs 之后就基本上复原了图像。使用不同的卷积层来还原，可以发现正如论文中所说的，对于内容图像，越底层的卷积层的复原效果就越好。

也可以尝试先将白噪声图像优化到风格图像，先观察捕捉到了什么层次的风格，再使用内容图像进行优化。

从内容图像开始生成的好处是只需要进行风格的优化，如果风格优化过度，那么可以采取提前停止（early stop）来获得不过度优化的生成图像。但由于整个生成过程中没有随机性，得到的图像都是相同的。

从白噪声开始生成的图像因为随机初始化就可以获得不同的生成图像。不过从结果上看，无论是从内容图像开始还是从白噪声开始，其得到的结果的视觉效果是接近的，没有哪一种方式的效果会更好的说法。

训练时，可以不断修改 $\alpha ,\beta$ 来控制图像和内容、风格的相关性。还可以通过修改内容图像和风格图像的比例，令风格图像的不同层次的纹理出现在生成图像中。比如下图就是不同内容和风格的比例所得到的图像。可以看到，从宏观的图案到微观的笔触都反映在了生成图像上。

最后贴出几张我感觉效果比较好的生成图片，这些图片使用了不同的图像大小比例和内容风格比例，但是始终达不到论文中那么好的效果。我推测可能是使用了更好的网络参数、在训练时改变图像比例先后捕捉不同层次的风格、对生成图像不同位置采用了不同的优化速率等等。