证明霍夫丁引理 Hoeffding Lemma
马尔可夫不等式(Markov's inequality)
\(X\ge0\) 为非负随机变量,\(t>0\) 为常数,则有
证:
指示器函数 \(I\lbrace A\rbrace=\begin{cases}1 &\text{if }A\\0&\text{else}\end{cases}\)
在随机变量中获取一个样本 \(X_0\),
- 若 \(X_0\ge t\),则 \(X_0/t\ge1=I\lbrace X_0\ge t\rbrace\),
- 若 \(X_0<t\),则 \(X_0/t\ge0=I\lbrace X_0\ge t\rbrace\),
即 \(X/t\ge I\lbrace X\ge t\rbrace\)
切比雪夫不等式(Chebyshev's inequality)
\(X\) 为随机变量,\(t>0\) 为常数,则有
证:
将 \((X-\mathbb EX)^2\) 和 \(t^2\) 代入马尔可夫不等式,得 \(\mathbb P[(X-\mathbb EX)^2\ge t^2]\le{\mathbb E(X-\mathbb EX)^2\over t^2}\)。整理即得到切比雪夫不等式。
推论:
设 \(X_i,i=1,2,\ldots,n\) 与 \(X\) 独立同分布,\(\bar X:=\frac1n\sum_i^nX_i\),则 \(\operatorname{Var}(\bar X)=\operatorname{Var}(X)/n\)
矩生成函数(moment generating function)
定义:\(M_X(\lambda):=\mathbb E\exp(\lambda X)\)
若 \(X_1,\ldots,X_n\) 相互独立,则
证:
切诺夫界(Chernoff bounds)
\(X\) 为随机变量,\(t\ge0\) 为常数,则有
证:
将 \(\exp[\lambda(X-\mathbb EX)]\) 和 \(\exp(\lambda t)\) 代入马尔可夫不等式,得 \(\mathbb P(\exp[\lambda(X-\mathbb EX)]\ge\exp(\lambda t))\le{\mathbb E\exp[\lambda(X-\mathbb EX)]\over\exp(\lambda t)}\)。令 \(\mathbb P(\exp[\lambda(X-\mathbb EX)]\ge\exp(\lambda t))\equiv\mathbb P(X-\mathbb EX\ge t)\),则要求 \(\lambda>0\)。对于 \(\lambda=0\),显然成立。因此选择右项对于 \(\lambda\ge0\) 的下界,整理即得到切诺夫界。
例:
正态分布,对于 \(X\sim\mathcal N(\mu,\sigma^2)\) 只需要在计算中加上常数 \(\mu\),因此只考虑 \(\mathcal N(0,\sigma^2)\)
多次伯努利试验
可以看出,将 \(M_X(\lambda)\) 化作 \(M_X(\lambda)\le\exp(f_X(\lambda))\) 的形式是很方便的,其中 \(f_X(\lambda)\) 是参数与 \(X\) 有关的函数。
霍夫丁引理(Hoeffding's lemma)
\(X\in[a,b]\) 为有界随机变量,对 \(\lambda\in\mathbb R\),有
证明:两种方法
若定义在 \([a,b]\) 上的 \(f(x)\) 为凸函数,则有
将 \(x\) 视为随机变量 \(X\) 加上期望得到
-
令 \(X\leftarrow X-\mathbb EX\),即变量减去期望,令期望变为零 \(\mathbb EX=0\)。选择函数 \(f(X)=\exp(\lambda X),\lambda\ge0\)。
并考虑将 \(M_X(\lambda)\) 化为 \(M_X(\lambda)\le\exp f_X(\lambda)\) 的形式。得到
\[\begin{align*} &&\mathbb E\exp(\lambda X)&\le{be^{\lambda a}-ae^{\lambda b}\over b-a}\\ &&&=e^{\lambda a}{b-ae^{\lambda(b-a)}\over b-a}\\ \text{let}&&f(\lambda)&:=\ln\left(e^{\lambda a}{b-ae^{\lambda(b-a)}\over b-a}\right)\\ &&&=\lambda a-\ln(b-a)+\ln(b-ae^{\lambda(b-a)})\\ \text{then}&&f'(\lambda)&=b\left(1-{b-a\over b-ae^{\lambda(b-a)}}\right)\\ &&f''(\lambda)&=(b-a)^2{-abe^{\lambda(b-a)}\over[b-ae^{\lambda(b-a)}]^2}\\ \text{because}&&(c+d)^2&\ge4cd,\ \forall c,d\in\mathbb R\\[1em] \text{therefore}&&[b-ae^{\lambda(b-a)}]^2&\ge-4abe^{\lambda(b-a)}\\[1em] &&f''(\lambda)&\le\frac{(b-a)^2}4\\ &&f(\lambda)&=f(0)+\lambda f'(0)+\frac12\lambda^2f^"(\theta\lambda),\text{ where }0\le\theta\le1\\ &&&\le\frac18\lambda^2(b-a)^2\\[1em] \text{finally}&&\mathbb E\exp(\lambda X)&\le\exp f(\lambda)\le\exp\left(\lambda^2(b-a)^2\over8\right) \end{align*} \] -
选择函数 \(f(X)=X^2\),\(\operatorname{Var}(X)=\mathbb EX^2-\mathbb E^2X\)。得到
\[\begin{align*} \operatorname{Var}(X)&=\mathbb EX^2-\mathbb E^2X\\ &\le{ba^2-ab^2+(b^2-a^2)\mathbb EX\over b-a}-\mathbb E^2X\\ &=-ab+(b+a)\mathbb EX-\mathbb E^2X\\ &\le\frac{(b-a)^2}4\\ \end{align*} \]\(\mathbb EX=(a+b)/2\) 时取等。
我们引入对数矩生成函数 \(f(\lambda)=\ln M_X(\lambda)=\ln\mathbb E\exp(\lambda X)\),用 \(t\) 代替 \(\lambda\) 表示和上面的方法不同。
\[\begin{align*} &&f'(t)&=\frac1{\mathbb E\exp(tX)}{\mathrm d\over\mathrm dt}\mathbb E\exp(tX)\\ &&&={\mathbb E[X\exp(tX)]\over\mathbb E\exp(tX)}\\ &&f''(t)&={\mathbb E[X^2\exp(tX)]\mathbb E\exp(tX)-\mathbb E^2[X\exp(tX)]\over\mathbb E^2\exp(tX)}\\ \text{let}&&E&:=\mathbb E\exp(tX)\\ \text{then}&&f''(t)&=\mathbb E\left[X^2{\exp(tX)\over E}\right]-\mathbb E\left[X{\exp(tX)\over E}\right]^2\\ \text{let}&&p'(Y)&:={\exp(tY)\over E}p(Y),\text{ and }\int_a^bp'(y)\mathrm dy\equiv1\\ \text{then}&&f''(t)&=\operatorname{Var}(Y)\le\frac{(b-a)^2}4\\ \text{therefore}&&f(t)&=f(0)+tf'(0)+\frac t2f''(\theta t),\text{ where }0\le\theta\le1\\ &&&\le\frac18t(b-a)^2\\ \text{finally}&&\mathbb E\exp(t X)&=\exp f(t)\le\exp\left(t^2(b-a)^2\over8\right) \end{align*} \]其中使用了概率分布为 \(\exp(tY)p(Y)/E\) 的新变量 \(Y\),且 \(Y\) 同样满足 \(Y\in[a,b]\)。
总之用不同的方法得出,\(M_X(\lambda)\le\exp(f_X(\lambda))\) 形式的结果。
霍夫丁不等式(Hoeffding's inequality)
\(X_i,i=1,\ldots,n\) 为独立有界随机变量,满足 \(X_i\in[a,b],-\infty<a\le b<\infty\),令 \(\mu:=\frac1n\sum_{k=1}^n(X_i-\mathbb EX_i)\),\(t\ge0\) 为常数,则
证:
在霍夫丁引理的基础上计算切诺夫界,只计算第一项,第二项同理
尝试理解这些不等式,已知这些不等式都是从马尔可夫不等式推出,先考察马尔可夫不等式。从证明过程上看,不等式 \(\mathbb P(X\ge t)\le{\mathbb EX\over t}\) 中,当 \(X<t\) 时 \(X\) 越接近零越好,当 \(X\ge t\) 时,\(X\) 越接近 \(t\) 越好;而从概率上,则意味着这两种情况对应的概率越大越好。
在计算切比雪夫不等式和切诺夫界时分别对随机变量 \(X\) 使用了变换 \(X^2\) 和 \(\exp(\lambda X)\)。变换有两个作用,一是使随机变量为非负值,二是使函数的分布发生变换,这一变换可以计算出来。
对标准正态分布和 \([-1,1]\) 上的均匀分布绘图,并作相应变换。其中蓝色线代表原始分布 \(X\),橙色线 **2 代表 \(X^2\),绿色线 exp 代表 \(\exp(\lambda X)\)。并且为不同变换下的 \(t\) 用不同的竖虚线表示。
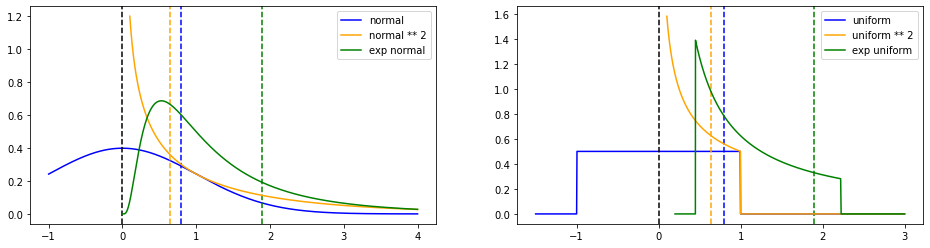
附代码
def inequality_draw(ax, name, f, low, high,
c_low, c_high, t=None, lamb=1, number=1000):
if t is not None:
ax.axvline(0, c='black', linestyle='--')
ax.axvline(t, c='blue', linestyle='--')
ax.axvline(t ** 2, c='orange', linestyle='--')
ax.axvline(np.exp(lamb * t), c='green', linestyle='--')
x = np.linspace(low, high, number)
ax.plot(x, f(x), label=name, color='blue')
y = np.linspace(np.sqrt(c_low[0]), np.sqrt(c_high[0]), number) ** 2
sy = np.sqrt(y)
ax.plot(y, 1 / (2 * sy) * (f(sy) + f(-sy)),
label=f'{name} ** 2',
color='orange')
y = np.exp(np.linspace(np.log(c_low[1]), np.log(c_high[1]), number))
ax.plot(y, 1 / (lamb * y) * f(np.log(y) / lamb),
label=f'exp {name}',
color='green')
ax.legend()
_, axes = plt.subplots(1, 2, figsize=(16, 4))
inequality_draw(axes[0], 'normal',
lambdify('x', S('1/sqrt(2*pi) * exp(-x^2/2)'), "numpy"),
-1, 4,
[0.1, 0.001], [4, 4],
t=0.8, lamb=0.8)
inequality_draw(axes[1], 'uniform',
lambda x: ((-1 < x) & (x < 1)) * 0.5,
-1.5, 3,
[0.1, 0.2], [3, 3],
t=0.8, lamb=0.8)
plt.show()



 浙公网安备 33010602011771号
浙公网安备 33010602011771号