变换域常用性质总结
目录
基础
分解
\[\begin{align*}
f_e(t)&=\frac12[f(t)+f(-t)]\\
f_o(t)&=\frac12[f(t)-f(-t)]\\
f_r(t)&=\frac12[f(t)+f^*(t)]\\
\mathrm jf_i(t)&=\frac12[f(t)-f^*(t)]
\end{align*}
\]
性质
\[\begin{align*}
线性&&\begin{cases}e_1(t)\to r_1(t)\\e_2(t)\to r_2(t)\end{cases}&\implies C_1e_1(t)+C_2e_2(t)\to C_1r_1(t)+C_2r_2(t)\\
时不变性&&e(t)\to r(t)&\implies e(t-t_0)\to r(t-t_0)\\[0.5em]
因果性&&r(t)&\ 只与\ t\le t_0\ 有关
\end{align*}
\]
卷积
\[\begin{align*}
r(t)=e(t)*h(t)&=\int^\infty_{-\infty}e(\tau)h(t-\tau)\mathrm d\tau\\
{\mathrm d\over\mathrm dt}[f_1(t)*f_2(t)]&=\left[{\mathrm d\over\mathrm dt}f_1(t)\right]*f_2(t)\\
f(t)*\delta^{(k)}(t-t_0)&=f^{(k)}(t-t_0)\\
\end{align*}
\]
\[\begin{align*}
y(n)&=x(n)*h(n)=\sum^\infty_{m=-\infty}x(m)h(n-m)\\
x(n)&=\frac1{x(0)}\left[y(n)-\sum_{m=0}^{n-1}h(m)x(n-m)\right]
\end{align*}
\]
以下卷积中 \(x(n)=x(n)\mu(n)\),为因果序列
\[\begin{align*}
a_1^n*a_2^n&={a_1^{n+1}-a_2^{n+1}\over1-a}\\
a^n*a^n&=(n+1)a^n\\
a^n*n&=\frac n{1-a}+{a(a^n-1)\over(1-a)^2}\\
n*n&=\frac16(n-1)n(n+1)\\
a_1^n\cos(\omega n+\theta)*a_2^n&={a_1^{n+1}\cos[\omega(n+1)+\theta-\varphi]-a_2^{n+1\cos(\theta-\varphi)}\over\sqrt{a_1^2+a_2^2-2a_1a_2\cos\omega}}
\end{align*}
\]
Fourier 变换
三角函数傅里叶级数
\[\begin{align*}
f(t)&=a_0+\sum_{n=1}^\infty[a_n\cos(n\omega_1t)+b_n\sin(n\omega_1t)]\\
a_0&=\frac1{T_1}\int^{t_0+T_1}_{t_0}f(t)\mathrm dt\\
a_n&=\frac2{T_1}\int^{t_0+T_1}_{t_0}f(t)\cos(n\omega_1t)\mathrm dt\\
b_n&=\frac2{T_1}\int^{t_0+T_1}_{t_0}f(t)\sin(n\omega_1t)\mathrm dt\\
\end{align*}
\]
指数傅里叶级数
\[\begin{align*}
f(t)&=\sum_{n=-\infty}^\infty F(n\omega_1)e^{\mathrm jn\omega_1t}\\
F_n=F(n\omega_1)&=\frac1{T_1}\int^{t_0+T_1}_{t_0}f(t)e^{-\mathrm jn\omega_1t}\mathrm dt\\
\end{align*}
\]
定义
\[\begin{align*}
f(t)&=\mathscr F^{-1}[F(\omega)]=\frac1{2\pi}\int_{-\infty}^\infty F(\omega)e^{\mathrm j\omega t}\mathrm d\omega\\
F(\omega)&=\mathscr F[f(t)]=\int^\infty_{-\infty}f(t)e^{-\mathrm j\omega t}\mathrm dt\\
\end{align*}
\]
性质
\[\begin{align*}
f(t)&&&F(\omega)\\\hline
1&&&2\pi\delta(\omega)\\
\delta(t)&&&1\\
\mu(t)&&&\pi\delta(\omega)+\frac1{\mathrm j\omega}\\
\operatorname{sgn}(t)&&&\frac2{\mathrm j\omega}\\
\cos(\omega_0t)&&&\pi[\delta(\omega+\omega_0)+\delta(\omega-\omega_0)]\\
\sin(\omega_0t)&&&\mathrm j\pi[\delta(\omega+\omega_0)-\delta(\omega-\omega_0)]\\
e^{\mathrm j\omega_0t}&&&2\pi\delta(\omega-\omega_0)\\
e^{-\alpha\vert t\vert}&&&\frac{2\alpha}{\alpha^2+\omega^2}\\\hline
\sum a_if_i(t)&&&\sum a_iF_i(\omega)\\
F(t)&&&2\pi f(-\omega)\\
f(at)&&&\frac1{\vert a\vert}F(\frac\omega a)\\
f(t+t_0)&&&F(\omega)e^{\mathrm j\omega t_0}\\
f(at+t_0)&&&\frac1{\vert a\vert}F(\frac\omega a)e^{\mathrm j\frac\omega at_0}\\
f(t)e^{\mathrm j\omega_0t}&&&F(\omega-\omega_0)\\\hline
f(t)\cos(\omega_0t)&&&\frac12[F(\omega+\omega_0)+F(\omega-\omega_0)]\\
f(t)\sin(\omega_0t)&&&\frac{\mathrm j}2[F(\omega+\omega_0)-F(\omega-\omega_0)]\\\hline
{\mathrm d^nf(t)\over\mathrm dt^n}&&&(\mathrm j\omega)^nF(\omega)\\
(-\mathrm jt)^nf(t)&&&{\mathrm d^nF(\omega)\over\mathrm d\omega^n}\\
\int^t_{-\infty}f(\tau)\mathrm d\tau&&&{F(\omega)\over\mathrm j\omega}+\pi F(0)\delta(\omega)\\
\pi f(0)\delta(t)+{f(t)\over-\mathrm jt}&&&\int_{-\infty}^\omega F(\upsilon)\mathrm d\upsilon\\\hline
f_1(t)*f_2(t)&&&F_1(\omega)F_2(\omega)\\
f_1(t)f_2(t)&&&\frac1{2\pi}F_1(\omega)*F_2(\omega)\\\hline
\sum_{n=-\infty}^\infty f(t)\delta(t-nT_s)&&&\frac1{T_s}\sum_{n=-\infty}^\infty F(\omega-n\omega_s)\\
\frac1{\omega_s}\sum_{n=-\infty}^\infty f(t-nT_s)&&&\sum_{n=-\infty}^\infty F(\omega)\delta(\omega-n\omega_s)\\\hline
R_{12}(\tau)&&&F_1(\omega)F_2^*(\omega)\\
R_{21}(\tau)&&&F_1^*(\omega)F_2(\omega)\\
R(\tau)&&&\vert F(\omega)\vert^2
\end{align*}
\]
与傅里叶级数
\[\begin{align*}
f_0(t)&=f(t)[\mu(t-t_0)-\mu(t-t_0-T_1)]\\
F_0(\omega)&=\int^{t_0+T_1}_{t_0}f(t)e^{-\mathrm j\omega t}\mathrm dt\\
F_n&=\left.\frac1{T_1}F_0(\omega)\right\vert_{\omega=n\omega_1}\\
\mathscr F[f(t)]&=2\pi\sum_{n=-\infty}^\infty F_n\delta(\omega-n\omega_1)\\
&={2\pi\over T_1}\sum_{n=-\infty}^\infty F_0(n\omega_1)\delta(\omega-n\omega_1)\\
\end{align*}
\]
Hilbert 变换关系
\[\begin{align*}
H(\mathrm j\omega)&=\mathscr F[h(t)\mu(t)]=R(\omega)+\mathrm jX(\omega)\\
R(\omega)&=\frac1\pi\int^\infty_{-\infty}{X(\lambda)\over\omega-\lambda}\mathrm d\lambda\\
X(\omega)&=-\frac1\pi\int^\infty_{-\infty}{R(\lambda)\over\omega-\lambda}\mathrm d\lambda\\
\end{align*}
\]
Laplace 变换
\[\begin{align*}
f(t)&=\mathscr L^{-1}[F(s)]=\frac1{\mathrm j2\pi}\int_{\sigma-\mathrm j\infty}^{\sigma+\mathrm j\infty} F(s)e^{st}\mathrm ds\\
F(s)&=\mathscr L[f(t)]=\int^\infty_0f(t)e^{-st}\mathrm dt\\
s&=\sigma+\mathrm j\omega
\end{align*}
\]
性质
\[\begin{align*}
f(t)&&&F(s)\\\hline
\delta(t)&&&1\\
\mu(t)&&&\frac1s\\
\cos(\omega t)&&&\frac s{s^2+\omega^2}\\
\sin(\omega t)&&&\frac\omega{s^2+\omega^2}\\
e^{at}&&&\frac1{s-a}\\
t^n,(n\in\mathbb Z^+)&&&\frac{n!}{s^{n+1}}\\
\cosh(at)&&&\frac s{s^2-a^2}\\
\sinh(at)&&&\frac a{s^2-a^2}\\\hline
\sum a_if_i(t)&&&\sum a_iF_i(s)\\
f(t-t_0)\mu(t-t_0)&&&F(s)e^{-st_0}\\
f(at)&&&\frac1aF(\frac sa)\\
f(t)e^{-at}&&&F(s+a)\\\hline
f(t)\cos(\omega t)&&&\frac12[F(s+\mathrm j\omega)+F(s-\mathrm j\omega)]\\
f(t)\sin(\omega t)&&&\frac{\mathrm j}2[F(s+\mathrm j\omega)-F(s-\mathrm j\omega)]\\\hline
{\mathrm d^nf(t)\over\mathrm dt^n}&&&s^nF(s)-\sum_{r=1}^ns^{n-r}f^{(r-1)}(0)\\
(-t)^nf(t)&&&{\mathrm d^nF(s)\over\mathrm ds^n}\\
\int^t_{-\infty}f(\tau)\mathrm d\tau&&&{F(s)\over s}+\frac{f^{(-1)}(0)}s\\
\frac{f(t)}t&&&\int_s^\infty F(p)\mathrm dp\\\hline
[f_1(t)\mu(t)]*[f_2(t)\mu(t)]&&&F_1(s)F_2(s)\\
f_1(t)f_2(t)&&&\frac1{\mathrm j2\pi}\int_{\sigma-\mathrm j\infty}^{\sigma+\mathrm j\infty} F_1(p)F_2(s-p)\mathrm dp\\
\end{align*}
\]
\[\begin{align*}
\lim_{t\to0}f(t)&=\lim_{s\to\infty}sF(s)\\
\lim_{t\to\infty}f(t)&=\lim_{s\to0}sF(s)\\
\end{align*}
\]
分式展开
\[\begin{align*}
F(s)&=\sum_{k=1}^n{K_k\over(s-p)^{n-k+1}}+{E(s)\over D(s)}\\
K_k&=\frac1{(k-1)!}\left[{\mathrm d^{k-1}\over\mathrm ds^{k-1}}(s-p)^nF(s)\right]_{s=p}\\
K_{k=1,n=1}&=\left.(s-p)F(s)\right\vert_{s=p}
\end{align*}
\]
\[\begin{align*}
H(s)&=K{\prod_{j=1}^M(s-z_j)\over\prod_{i=1}^N(s-p_i)}\\
H(\mathrm j\omega)&=\left.H(s)\right\vert_{s=\mathrm j\omega}=K{\prod_{j=1}^M(\mathrm j\omega-z_j)\over\prod_{i=1}^N(\mathrm j\omega-p_i)}\\
&=K{\prod_{j=1}^MM_je^{\mathrm j\theta_j}\over\prod_{i=1}^NN_ie^{\mathrm j\psi_i}}\\
&=K{\prod_jM_j\over\prod_iN_i}e^{\mathrm j\left[\sum_j\theta_j-\sum_i\psi_i\right]}\\
\vert H(\mathrm j\omega)\vert&=K{\prod_jM_j\over\prod_iN_i}\\
\varphi(\omega)&=\sum_j\theta_j-\sum_i\psi_i
\end{align*}
\]
稳定条件
\[\begin{align*}
\int^\infty_{-\infty}\vert h(t)\vert\mathrm dt&<\infty\\
\forall p&[\operatorname{Re}(p)<0]
\end{align*}
\]
z 变换
\[\begin{align*}
X(z)&=\mathscr Z[x(n)]=\sum_{n=-\infty}^\infty x(n)z^{-n}\\
x(n)&=\frac1{\mathrm j2\pi}\oint_CX(z)z^{n-1}\mathrm dz,\\
&\quad\ \ \text{$C$ 为包含 $X(z)z^{n-1}$ 所有极点的逆时针闭合积分路线}
\end{align*}
\]
性质
\[\begin{align*}
x(n)&&&X(z)&\\\hline
\delta(n)&&&1\\
\mu(n)&&&\frac1{1-z^{-1}}&\vert z\vert>1\\
n\mu(n)&&&\frac z{(z-1)^2}&\vert z\vert>1\\
n^2\mu(n)&&&\frac{z(z+1)}{(z-1)^3}&\vert z\vert>1\\
a^n\mu(n)&&&\frac z{z-a}&\vert z\vert>\vert a\vert\\
na^n\mu(n)&&&\frac{az}{(z-a)^2}&\vert z\vert>\vert a\vert\\
n^2a^n\mu(n)&&&\frac{az(z+a)}{(z-a)^3}&\vert z\vert>\vert a\vert\\
{(n+1)\cdots(n+m)\over m!}a^n\mu(n)&&&{z^{m+1}\over(z-a)^{m+1}}&\vert z\vert>\vert a\vert\\
{n(n-1)\cdots(n-m+1)\over m!}a^{n-m}\mu(n)&&&\frac z{(z-a)^{m+1}}\\
{n(n-1)\cdots(n-m+1)\over m!}\mu(n)&&&{z\over(z-1)^{m+1}}\\\hline
\cos(\omega n)\mu(n)&&&\frac12\left(\frac z{z-e^{-\mathrm j\omega}}+\frac z{z-e^{\mathrm j\omega}}\right)={z(z-\cos\omega)\over z^2-2z\cos\omega +1}&\vert z\vert>1\\
\sin(\omega n)\mu(n)&&&\frac{\mathrm j}2\left(\frac z{z-e^{-\mathrm j\omega}}-\frac z{z-e^{\mathrm j\omega}}\right)={z\sin\omega\over z^2-2z\cos\omega +1}&\vert z\vert>1\\
\beta^n\cos(\omega n)\mu(n)&&&{z(z-\beta\cos\omega)\over z^2-2\beta z\cos\omega+\beta^2}&\vert z\vert>\vert\beta\vert\\
\beta^n\sin(\omega n)\mu(n)&&&{\beta z\sin\omega\over z^2-2\beta z\cos\omega+\beta^2}&\vert z\vert>\vert\beta\vert\\
\cosh(\omega n)\mu(n)&&&{z(z-\cosh\omega)\over z^2-2z\cosh\omega +1}\\
\sinh(\omega n)\mu(n)&&&{z\sinh\omega\over z^2-2z\cosh\omega +1}\\\hline
\frac1n\mu(n-1)&&&\ln\left(\frac z{z-1}\right)\\
{a^n\over n!}\mu(n)&&&e^{a/z}\\
\frac1{(2n)!}\mu(n)&&&\cosh\left(z^{-1/2}\right)\\
{(\ln a)^n\over n!}\mu(n)&&&a^{1/z}\\\hline
\sum a_ix_i(n)&&&\sum a_iX_i(z)&\bigcap_iR(X_i)\\
x(n-m)&&&X(z)z^{-m}&R(X)\\
x(n)a^n&&&X(z/a)&\vert a\vert R(X)\\\hline
\operatorname{Re}[x(n)]&&&\frac12[X(z)+X^*(z^*)]&R(X)\\
\operatorname{Im}[x(n)]&&&\frac1{\mathrm j2}[X(z)-X^*(z^*)]&R(X)\\
x^*(n)&&&X^*(z^*)&R(X)\\
x(-n)&&&X(z^{-1})&R[X(z^{-1})]\\\hline
nx(n)&&&-z{\mathrm dX(z)\over\mathrm dz}&R(X)\\
\frac{x(n)}{(n+a)}&&&-z^a\int^z_0{X(\upsilon)\over\upsilon^{a+1}}\mathrm d\upsilon\\
\sum_{k=0}^nx(k)&&&\frac z{z-1}X(z)\\\hline
x(n)*h(n)&&&X(z)H(z)&R(X)\cap R(H)\\
x(n)h(n)&&&\frac1{\mathrm j2\pi}\oint_CX(\upsilon)H\left(\frac z\upsilon\right){\mathrm d\upsilon\over \upsilon}&R(X)\cdot R(H)
\end{align*}
\]
\[\begin{align*}
x(0)&=\lim_{z\to\infty}X(z)\\
x(\infty)&=\lim_{z\to1}(z-1)X(z)\\
\end{align*}
\]
分式展开
\[\begin{align*}
X(z)&=\sum_{k=0}^{n-1}{K_kz\over(z-p)^{n-k}}+{E(z)\over D(z)}+A\\
K_k&=\frac1{k!}\left[{\mathrm d^k\over\mathrm dz^k}{(z-p)^n\over z}X(z)\right]_{z=p}\\
K_{k=n=1}&=\left.{z-p\over z}X(z)\right\vert_{z=p}\\
A&=X(0)
\end{align*}
\]
收敛条件
\[\begin{align*}
\sum_{n=-\infty}^\infty\vert x(n)\vert&<\infty\\
z&\in R(X)
\end{align*}
\]
离散时间 Fourier 变换(DTFT)
\[\begin{align*}
X(e^{\mathrm j\omega})&=X(z)\vert_{z=e^{\mathrm j\omega}}=\sum_{n=-\infty}^\infty x(n)e^{-\mathrm jn\omega}\\
x(n)&=\frac1{2\pi}\int_{-\pi}^\pi X(e^{\mathrm j\omega})e^{\mathrm jn\omega}\mathrm d\omega,\\
\end{align*}
\]
实序列对称关系
\[\begin{align*}
X(e^{\mathrm j\omega})&=X^*(e^{-\mathrm j\omega})\\
X_{\operatorname{re}}(e^{\mathrm j\omega})&=X_{\operatorname{re}}(e^{-\mathrm j\omega})\\
X_{\operatorname{im}}(e^{\mathrm j\omega})&=-X_{\operatorname{re}}(e^{-\mathrm j\omega})\\
\vert X(e^{\mathrm j\omega})\vert&=\vert X(e^{-\mathrm j\omega})\vert\\
\arg X(e^{\mathrm j\omega})&=-\arg X(e^{-\mathrm j\omega})
\end{align*}
\]
性质
\[\begin{align*}
x(n)&&&X(e^{\mathrm j\omega})\\\hline
x(-n)&&&X(e^{-\mathrm j\omega})\\
x(n-n_0)&&&X(e^{-\mathrm j\omega})e^{-\mathrm j\omega n_0}\\
x(-n)e^{\mathrm j\omega_0n}&&&X\left(e^{\mathrm j(\omega-\omega_0)}\right)\\
nx(n)&&&\mathrm j{\mathrm dX(e^{\mathrm j\omega})\over\mathrm d\omega}\\
x(n)*h(n)&&&X(e^{\mathrm j\omega})H(e^{\mathrm j\omega})\\
x(n)h(n)&&&\frac1{2\pi}\int_{-\pi}^\pi X(e^{\mathrm j\upsilon})H\left(e^{\mathrm j(\omega-\upsilon)}\right)\mathrm d\upsilon
\end{align*}
\]
\[\begin{align*}
\sum_{n=-\infty}^\infty x(n)h^*(n)&=\frac1{2\pi}\int_{-\pi}^\pi X(e^{\mathrm j\omega})H^*(e^{\mathrm j\omega})\mathrm d\omega
\end{align*}
\]
其余参考 z 变换,令 \(z=e^{\mathrm j\omega}\)。
收敛条件
\[\begin{align*}
\sum_{n=-\infty}^\infty\vert x(n)\vert&<\infty\\
e^{\mathrm j\omega}&\in R(X)
\end{align*}
\]
离散 Fourier 变换(DFT)
\[\begin{align*}
X(k)&=\left.X(e^{\mathrm j\omega})\right\vert_{\omega=2\pi k/N}=\sum_{n=0}^{N-1}x(n)e^{-\mathrm j2\pi kn/N}\\
x(n)&=\frac1N\sum_{k=0}^{N-1}X(k)e^{\mathrm j2\pi kn/N}\\
X(e^{\mathrm j\omega})&=\sum_{k=0}^{N-1}X(k)\Phi(\omega-{2\pi k\over N})\\
\Phi(\omega)&={\sin\left(\frac{\omega N}2\right)\over N\sin\left(\frac\omega2\right)}e^{-\mathrm j\omega\frac{N-1}2}
\end{align*}
\]
\[\begin{align*}
\pmb X&=\pmb A\pmb x\\
\pmb A_{i,j}&=e^{-\mathrm j2\pi ij/N}
\end{align*}
\]
圆周卷积
\[\begin{align*}
x(n)Ⓝh(n)=\sum_{m=0}^{N-1}x(m)h(\langle n-m\rangle_N)
\end{align*}
\]
性质
\[\begin{align*}
x(n)&&&X(k)\\\hline
x^*(n)&&&X^*(\langle -k\rangle_N)\\
x^*(\langle -n\rangle_N)&&&X^*(k)\\
x_{\operatorname{re}}(n)&&&X_{\operatorname{cs}}(k)=\frac12[X(k)+X^*(\langle -k\rangle_N)]\\
\mathrm jx_{\operatorname{im}}(n)&&&X_{\operatorname{ca}}(k)=\frac12[X(k)-X^*(\langle -k\rangle_N)]\\
x_{\operatorname{cs}}(n)&&&X_{\operatorname{re}}(k)\\
x_{\operatorname{ca}}(n)&&&\mathrm jX_{\operatorname{im}}(k)\\\hline
x(\langle n-n_0\rangle_N)&&&X(k)e^{-\mathrm j2\pi kn_0/N}\\
x(n)e^{\mathrm j2\pi k_0n/N}&&&X(\langle k-k_0\rangle_N)\\
X(n)&&&Nx(\langle -k\rangle_N)\\
x(n)Ⓝh(n)=\sum_{m=0}^{N-1}x(m)h(\langle n-m\rangle_N)&&&X(k)H(k)\\
x(n)h(n)&&&\frac1NX(k)ⓃH(k)=\frac1N\sum_{m=0}^{N-1}X(m)H(\langle k-m\rangle_N)\\
\end{align*}
\]
\[\begin{align*}
\sum_{n=0}^{N-1}\vert x(n)\vert^2=\frac1N\sum_{n=0}^{N-1}\vert X(k)\vert^2
\end{align*}
\]
使用 Python Sympy
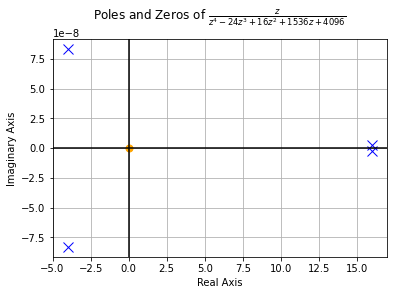
画出极点零点
from sympy.abc import z
from sympy.physics.control.control_plots import pole_zero_plot
from sympy.physics.control.lti import TransferFunction
tf = TransferFunction(z, z**4 - 24*z**3 + 16*z**2 + 1536*z + 4096, z)
pole_zero_plot(tf)
# t = s / (s-16)**2 / (s+4)**2
# tf = TransferFunction(*fraction(cancel(t)), var)
# pole_zero_plot(tf)
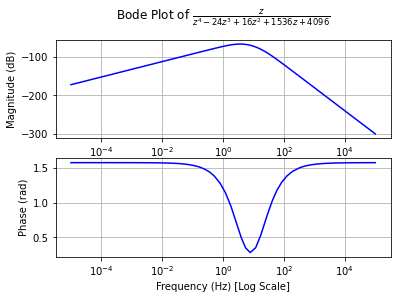
幅度谱和相位谱
from sympy.abc import z
from sympy.physics.control.control_plots import pole_zero_plot
from sympy.physics.control.lti import TransferFunction
tf = TransferFunction(z, z**4 - 24*z**3 + 16*z**2 + 1536*z + 4096, z)
bode_plot(tf, initial_exp=-5, final_exp=5)
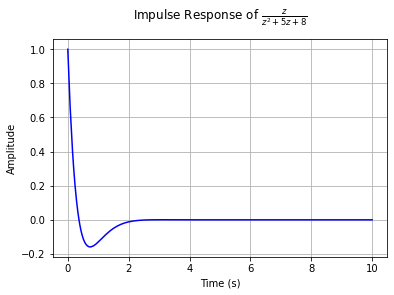
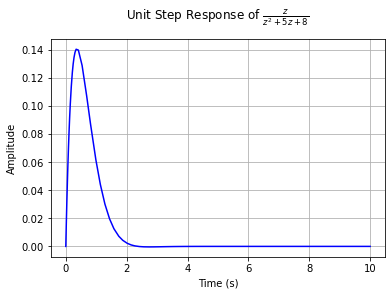
冲激响应、阶跃响应、斜坡响应
from sympy.abc import z
from sympy.physics.control.control_plots import (impulse_response_plot,
step_response_plot,
ramp_response_plot)
from sympy.physics.control.lti import TransferFunction
tf = TransferFunction(z, z**2 + 5*z + 8, z)
impulse_response_plot(tf)
step_response_plot(tf)
ramp_response_plot(tf, slope=2)
分解 z 变换
from sympy import *
from sympy.abc import z
from sympy.physics.control.lti import TransferFunction
from collections import Counter
def apart_z(t, var):
tf = TransferFunction.from_rational_expression(t, var)
poles = tf.poles()
pole_counts = Counter(poles)
result = t.subs({var: 0})
for p, n in pole_counts.items():
t_p = (var-p)**n / var * t
for k in range(n):
t_k = diff(t_p, var, k)
K_k = t_k.subs({var: p}) / factorial(k)
result += K_k * var / (var-p)**(n-k)
# result = sum((
# var / (var-p)**(n-k) / factorial(k) *
# diff((var-p)**n / var * t, var, k).subs({var: p})
# for k in range(n) for p, n in pole_counts.items()
# ), start=t.subs({var: 0}))
return result
测试
>>> t = z / (z-16)**2 / (z+4)**2
>>> h = apart_z(t, z)
>>> e = Eq(t, h)
>>> simplify(e)
True
分解 Laplace 变换同理,只需修改 for k in range(n) 内的代码即可。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号