算法导论 Introduction to Algorithms #算法基础

目录

算法基础

分析算法

  • 循环不变式

设计算法

  • 分治法

练习

  • 线性查找的平均检查次数

    最好 1 次，最坏 n 次，平均 \(\frac{n+1}{2}\) 次，\(f(n) = \Theta(n)\)。

  • 使任何算法的最好情况运行时间提高的办法

    将最好情况总结，并作为算法的特例实现。但是不应该将函数的最好情况作为判断函数效率的指标看待。

  • 归并算法 MERGE 过程结束的两种实现

    1. 使用哨兵

      MERGE 操作会选择更小的数填充数组，理论上可以使用 \(\infty\) 使下标不会越界，由于编程时没有真正的无穷，只能使用最大值代替，这要求原数组中没有最大值。

      void merge(int[] array, int low, int mid, int high)
{
    int len1 = mid - low, len2 = high - mid;
    int[] a1 = new int[len1 + 1];
    int[] a2 = new int[len2 + 1];
    for (int i = 0; i != len1; ++i) a1[i] = array[low + i];
    for (int i = 0; i != len2; ++i) a2[i] = array[mid + i];
    
    a1[len1] = Integer.max();
    a2[len2] = Integer.max();
    
    // merge
    for (int i = 0, j = 0, k = low; k != high; ++k) {
        array[k] = a1[i] <= a2[j] ? a1[i++] : a2[j++];
    }
}

    2. 进行下标越界检查

      比较 i, j != mid, high。

      i, j 分别达到 mid, high 是有先后的，因此需要在之后继续遍历未完结的数组。

      void merge(int[] array, int low, int mid, int high)
{
    int len1 = mid - low, len2 = high - mid;
    int[] a1 = new int[len1];
    int[] a2 = new int[len2];
    for (int i = 0; i != len1; ++i) a1[i] = array[low + i];
    for (int i = 0; i != len2; ++i) a2[i] = array[mid + i];
    
    // merge
    int i = 0, j = 0, k = low;
    while (i != len1 && j != len2) array[k++] = a1[i] <= a2[j] ? a1[i++] : a2[j++];
    while (i != len1) array[k++] = a1[i++];
    while (j != len2) array[k++] = a2[j++];
}

  • 证明

    \[\text{if } n = 2 ^ k, T(n) = \begin{cases} 2 & n = 2, \\[2ex] 2T(n/2) + n & n = 2 ^ k, k > 1, \end{cases} \\[2ex] \text{then } T(n) = n \lg n. \]

    \[\begin{align*} T(n) &= T(2^k) \\[2ex] &= 2T(2^{k-1}) + 2^k \\[2ex] &= 4T(2^{k-2}) + 2^{k} + 2^k \\[2ex] &= \cdots \\[2ex] &= 2^{k-1}T(2) + 2^k + \cdots + 2^k \\[2ex] &= k \cdot 2^k \\[2ex] &= n \lg n. \end{align*} \]

  • 将插入排序视为一个递归过程

    为了排序 a[0..n]（0..n 不包括 n），递归地排序 a[0..n-1]，将 a[n-1] 插入已排序的数组。

    由于 a[0..n-1] 有序，可以使用二分搜索获取插入位置，该算法稳定。

    public static void insertSort(int[] array, int n) {
    if (n > array.length) n = array.length;
    if (n <= 0) return;
    // sort [begin..end-1]
    insertSort(array, n - 1);
    // find
    int low = 0, high = n - 1;
    int target = array[high];
    while (low != high) {
        int mid = ((high - low) >> 1) + low;
        if (array[mid] <= target)
            low = mid + 1;
        else
            high = mid;
    }
    // 此时 array[high-1] <= target < array[high]
    // insert
    for (int i = n - 1; i != high; --i) array[i] = array[i - 1];
    array[high] = target;
}

    最坏情况为每次都插入首位，即数组完全递减，因此

    \[T(n) = \begin{cases} 1 & n = 1, \\[2ex] T(n-1) + \lg n + n & n \ne 1. \\ \end{cases} \]

  • 给定 n 个整数的集合 \(S\) 和另一个整数 \(n\)，给出 \(T(n)=\Theta(n \lg n)\) 的算法

    // T(n) = n lg n 修改元素
bool findAddPair(vector<int> &s, int n) {
    auto begin = s.begin(), end = s.end();
    sort(begin, end);
    for (int val : s) {
        if (binary_search(begin++, end, val - n)) return true;
    }
    return false;
}

    // T(n) = n 额外n哈希空间
bool findAddPair(const vector<int> &s, int n) {
    unordered_set<int> set;
    for (int val : s) {
        if (set.count(val - n)) return true;
        set.emplace(val);
    }
    return false;
}

思考题

  • 在归并排序中对小数组使用插入排序

    对长度为 \(k\) 的 \(\frac nk\) 个子表使用使用插入排序，再用标准的合并机制合并这些子表。

    1. 插入排序最坏情况为 \(\Theta(n^2)\)，可以在 \(T(n)=\frac{n}{k}\Theta(k^2)=\Theta(nk)\) 完成排序

    2. 归并排序最坏情况为 \(\Theta(n \lg n)\)，使用插入排序辅助后

      \[\begin{align*} & \frac n{2^p} \le k, \frac n{2^{p-1}} > k \\[2ex] \to & \lg\frac nk \le p < \lg\frac nk+ 1 \\[2ex] \to & p = \lceil \lg\frac nk \rceil \end{align*} \]

      \[\begin{align*} T(n) &= \begin{cases} \Theta(n^2) & n \le k, \\[2ex] 2T(n/2) + cn & n > k, \end{cases} \\[2ex] T(n) &= 2T(n/2) + cn \\[2ex] &= 4T(n/4) + cn + cn \\[2ex] &= \cdots \\[2ex] &= \Theta(nk) + cn\lg\frac nk \\[2ex] &= \Theta(nk) + \Theta(n\lg\frac nk). \end{align*} \]

      \(n\) 足够大时，求导有

      \[c_1 n = c_2 \frac nk, \\[2ex] k = \frac{c_2}{c_1}. \]

      解为 \(k\) 的取值。

      验证 \(k\) 与 \(n\) 无关（\(n\) 足够大时）：

      import numpy as np
import matplotlib.pyplot as plt
from time import perf_counter
from functools import wraps

def timethis(func):
    @wraps(func)
    def wrapper(*args, **kwargs):
        s = perf_counter()
        func(*args, **kwargs)
        t = perf_counter() - s

        return t
    return wrapper

def insertion_sort(arr):
    count = arr.size;
    if count <= 1: return
    i = 1
    while i != count:
        target = arr[i]
        low, high = 0, i
        while low != high:
            mid = (high + low) // 2
            if arr[mid] <= target:
                low = mid + 1
            else:
                high = mid
        j = i
        while j != high:
            arr[j] = arr[j - 1]
            j -= 1
        arr[high] = target
        i += 1

@timethis
def merge_sort(arr, k):
    a = arr
    count = a.size;
    if count <= 1: return
    b = np.zeros_like(a)
    if count <= k:
        insertion_sort(arr)
        return

    start = 0
    while start < count:
        insertion_sort(arr[start:start + k])
        start += k
    seg = k
    while seg < count:
        start = 0
        while start < count:
            low, high, mid = start, min(start + (seg * 2), count), min(start + seg, count)
            i, j, k = low, mid, low
            while i != mid and j != high:
                if a[j] < a[i]:
                    b[k] = a[j]
                    j += 1
                else:
                    b[k] = a[i]
                    i += 1
                k += 1
            while i != mid:
                b[k] = a[i]
                k += 1
                i += 1
            while j != high:
                b[k] = a[j]
                k += 1
                j += 1
            start += seg * 2
        a, b = b, a
        seg *= 2
    if b is arr:
        arr[:] = a

def main():
    for k in range(10, 100, 10):
        ns = np.array([5_000, 10_000, 50_000, 100_000])
        ts = np.empty_like(ns, dtype=np.float64)
        for i, n in enumerate(ns):
            ts[i] = avg_time(n, k)
        plt.plot(np.log(ns), ts, label=str(k))
        print(ts)
    plt.legend()
    plt.show()

      通过改变 \(k\) 和数组长度，随着数组长度的变化（\(5000 \to 2^{24}\)）， \(k\) 没有大幅改变，在此环境上可以认为 \(k\) 在 \((32,34)\) 附近。

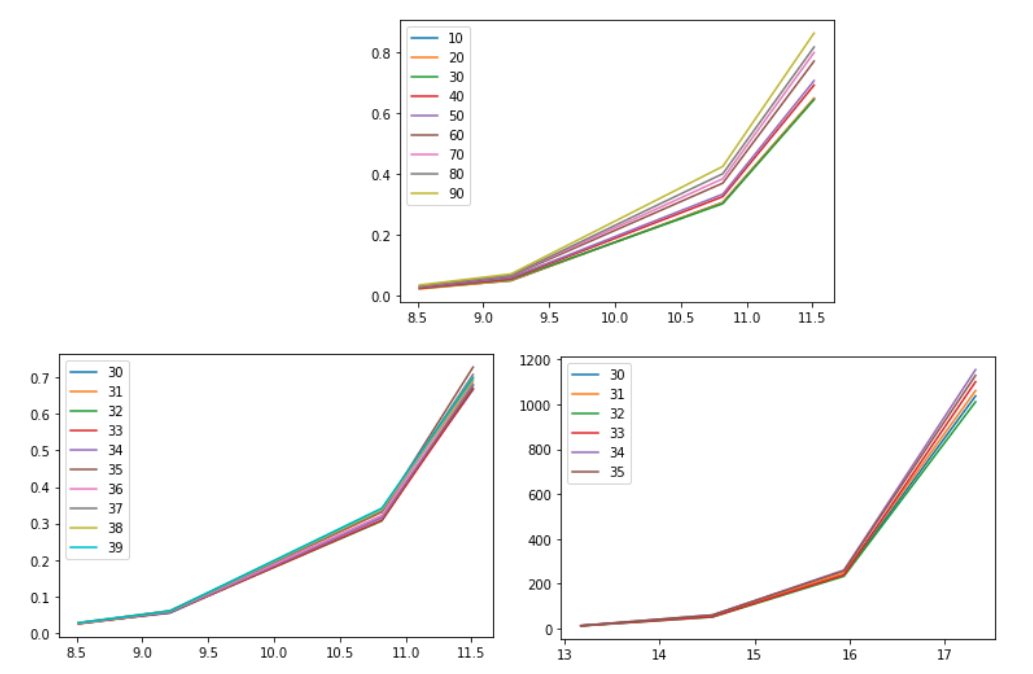
  • 霍纳（Horner）规则的正确性

    int y = 0;
for (int i = n; i >= 0; --i) y = a[i] + x * y;

    \[P(x) = \sum^n_{k=0}a_k x^k = a_0 + x(a_1 + x(a_2 + \cdots + x(a_{n-1} + xa_n)\cdots)) \]

    数学归纳法（循环不变式）证明：

    \[\begin{align*} \text{若 } & P_i(x) = \sum_{k=i}^{n}a_{k} x^{k-i}, \\ \text{则 } & P_{i-1}(x) = a_{i-1} + xP_i(x) = a_{i-1} + \sum_{k=i}^{n}a_{k} x^{k- i+1} = \sum_{k=i-1}^{n}a_k x^{k-(i-1)}. \\[2ex] \text{由于 } & P_n(x) = a_n = \sum_{k=n}^{n}a_k x^{k-n}, \\ \text{所以 } & P(x) = P_0(x) = \sum^n_{k=0}a_{k} x^{k}. \end{align*} \]

    可以取 \(P_{n+1} = 0\)

    可以计算机系统相关联

    # 1
int y = 0;
for (int i = n; i >= 0; --i) y = a[i] + x * y;

# 2
int y = 0;
int p = 1;
for (int i = 0; i <= n; ++i) {
    y += p * a[i];
    p *= x;
}

    由于 #2 做了两次乘法一次加法，#1 只做了一次乘法一次加法，#1 效率会更高。

  • 逆序对

    • 插入排序与逆序对数量的关系

      设 a[n] 与 a[0..n-1] 构成 \(k_n\) 个逆序对，则逆序对数量和为 \(K = \sum_{i=1}^n k_i\)，排序 a[0..n-1] 对 \(k_n\) 没有影响。

      \[\begin{align*} T(n) &= \begin{cases} 1 & n = 1, \\[2ex] T(n-1) + \lg n + k_n & n \ne 1, \\[2ex] \end{cases} \\[2ex] T(n) &= \lg(n!) + K. \end{align*} \]

      其中 \(\lg(n!)\) 为二分搜索消耗，\(K\) 为移动元素消耗。

      ns = np.array(2 << np.arange(10, 28))
ts = np.empty_like(ns, dtype=np.float64)
facts = np.empty_like(ts)

for i, n in enumerate(ns):
    a = np.arange(1, n + 1)
    facts[i] = np.sum(np.log2(a))
    ts[i] = insertion_sort(a)

plt.plot(np.arange(ts.size), ts / (np.log2(ns) * ns), label='log')
plt.plot(np.arange(ts.size), ts / facts , label='fact')
plt.legend()
plt.show()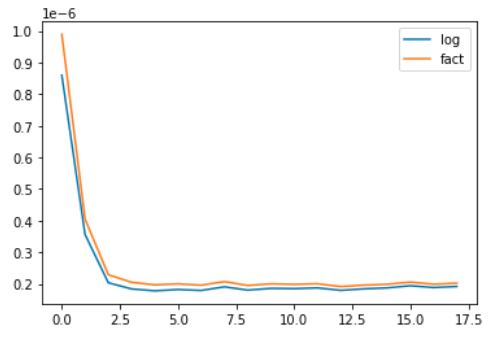

      随着数组长度的增加，对已排序数组的插入排序耗时与 \(\lg(n!),n \lg n\) 接近。事实上 \(\lg(n!),n \lg n\) 两者也很接近。\(n>300\) 后，两者的商就小于 \(1.2\) 了，\(n>30000\) 后，两者的商就小于 \(1.1\) 了。

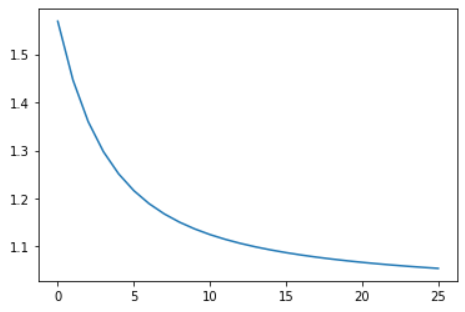
    • 给出 \(\Theta(n \lg n)\) 的求逆序对数量的算法

      修改归并排序

      逆序对数量等于两个子数组中的逆序对数量和两个子数组之间的逆序对数量。

      当 a1[i] > a2[j] 时，表明 a1[i..mid] > a2[j]，所以两个子数组之间的逆序对数为出现 a1[i] > a2[j] 时 mid - i 的和。

      // 递归

int invasions_count(vector<int> &arr, int low, int high)
{
    if (low >= high) return 0;
    int mid = ((high - low) >> 1) + low;
    int count = invasions_count(arr, low, mid) +
                invasions_count(arr, mid, high);
    count += invasions_merge(arr, low, mid, high);
    return count;
}

int invasions_merge(vector<int> &arr, int low, int mid, int high)
{
    int len1 = mid - low, len2 = high - mid;
    vector<int> a1(len1);
    vector<int> a2(len2);
    for (int i = 0; i != len1; ++i) a1[i] = arr[low + i];
    for (int i = 0; i != len2; ++i) a2[i] = arr[mid + i];
    
    int count = 0;
    // merge
    int i = 0, j = 0, k = low;
    while (i != len1 && j != len2) {
        if (a1[i] > a2[j]) {
            arr[k++] = a2[j++];
            // 只需要在这里计数即可
            count += len1 - i;
        } else {
            arr[k++] = a1[i++];
        }
    }
    while (i != len1) arr[k++] = a1[i++];
    while (j != len2) arr[k++] = a2[j++];
    return count;
}

      // 迭代

int invasions_count(vector<int> &a)
{
    int size = a.size();
    if (size <= 1) return 0;
    
    vector<int> b(size);

    int count = 0;
    for (int seg = 1; seg < size; seg <<= 1) {
        for (int start = 0; start < size; start += seg << 1) {
            int low = start;
            int mid = min(start + seg, size);
            int high = min(start + (seg << 1), size);
            int i = low, j = mid, k = low;
            while (i != mid && j != high) {
                if (a[i] > a[j]) {
                    b[k++] = a[j++];
                    // 只需要在这里计数即可
                    count += mid - i;
                } else {
                    b[k++] = a[i++];
                }
            }
            while (i != mid) b[k++] = a[i++];
            while (j != high) b[k++] = a[j++];
        }
        swap(a, b);
    }

   	return count;
}

函数记号

定义 名称 类比
\(\Theta(g(n)) = \{ f(n): \exists c_1, c_2,N>0, \forall n \ge N, \text{有 } 0 \le c_1 g(n) \le f(n) \le c_2 g(n) \}\) 渐进确界 \(f = g\)
\(O(g(n)) = \{ f(n): \exists c,N>0, \forall n \ge N, \text{有 } 0 \le f(n) \le c g(n) \}\) 渐进上界 \(f \le g\)
\(\Omega(g(n)) = \{ f(n): \exists c, N>0, \forall n \ge N, \text{有 } 0 \le c g(n) \le f(n) \}\) 渐进下界 \(f \ge g\)
\(o(g(n)) = \{ f(n): \forall c, \exists N>0, \forall n \ge N, \text{有 } 0 \le f(n) \lt c g(n) \}\) 非渐进紧确的上界 \(f \lt g\)
\(\omega(g(n)) = \{ f(n): \forall c, \exists N>0, \forall n \ge N, \text{有 } 0 \le c g(n) \lt f(n) \}\) 非渐进紧确的下界 \(f \gt g\)

  • 传递性

    \[\begin{align*} f(n) = \Theta(g(n)) \wedge g(n) = \Theta(h(n)) &\to f(n) = \Theta(h(n)), \\ f(n) = O(g(n)) \wedge g(n) = O(h(n)) &\to f(n) = O(h(n)), \\ f(n) = \Omega(g(n)) \wedge g(n) = \Omega(h(n)) &\to f(n) = \Omega(h(n)), \\ f(n) = o(g(n)) \wedge g(n) = o(h(n)) &\to f(n) = o(h(n)), \\ f(n) = \omega(g(n)) \wedge g(n) = \omega(h(n)) &\to f(n) = w(h(n)). \\ \end{align*} \]

  • 自反性

    \[\begin{align*} f(n) &= \Theta(f(n)), \\ f(n) &= O(f(n)), \\ f(n) &= \Omega(f(n)). \end{align*} \]

  • 对称性

    \[f(n) = \Theta(g(n)) \iff g(n) = \Theta(f(n)). \]

  • 转置对称性

    \[\begin{align*} f(n) = O(g(n)) &\iff g(n) = \Omega(f(n)), \\ f(n) = o(g(n)) &\iff g(n) = \omega(f(n)). \\ \end{align*} \]

\(\lg(n!) = \Theta(n\lg n)\)

\(\lg^bn=o(n^a),a>0\)

\(n! = \sqrt{2 \pi n}(\frac n{\rm e})^n(1+\Theta(\frac 1n))\)

\(\lg^*n = \min\{ i \ge 0: \lg^{(i)}n \le 1 \}\)

若 \(\exists k[f(n) = O(n^k)]\)，则称 \(f(n)\) 多项式有界；若 \(\exists k[f(n) = O(\lg^kn)]\)，则称 \(f(n)\) 多对数有界。

练习

  • 证明：若 \(f(n), g(n)\) 为渐进非负函数，\(\max(f(n), g(n)) = \Theta(f(n) + g(n))\)

    \[\begin{cases} f(n) + g(n) \ge \max(f(n), g(n)) \\ \frac{f(n) + g(n)}{2} \le \max(f(n), g(n)) \\ \end{cases} \implies \max(f(n), g(n)) = \Theta(f(n) + g(n)). \]

  • 证明：$$\forall a,b \in \mathbb R(b > 0 \to (n+a)^b = \Theta(n^b))$$

    \[\begin{align*} a \ge 0, \\ & (n+a)^b = \sum_{k=0}^{b}\binom{b}{k}n^{b-k}a^{k}, \\ & \text{let } n^b > \sum_{k=1}^{b}\binom{b}{k}n^{b-k}a^{k}, \\ & \sum_{k=1}^{b}\binom{b}{k}\frac{a^{k}}{n^k} < 1 \\ & \text{let }n > N = \binom{b}{[k/2]} \cdot ab, \text{then } 2n^b > (n+a)^b.\\ a < 0, \\ & \text{let } n' = n + a, n = n' - a, \text{then} -a > 0. \end{align*} \]

    \[\begin{align*} n+a \le n + \lvert a \rvert \le 2n, &\text{ when }n \ge \lvert a \rvert \\ n+a \ge n - \lvert a \rvert \ge \frac 12n, &\text{ when }n \ge 2\lvert a \rvert \\\hline 0 \le (\frac 12)^bn^b \le (n+a)^b \le 2^bn^b, &\text{ when } n \ge 2\lvert a \rvert \end{align*} \]

  • \(T(N)\) 至少为 \(O(n^2)\) 无意义

    \(O(n^2)\) 表示的所有渐进时间在 \(n^2\) 以下的函数

  • 证明：\(f(n) = \Theta(g(n)) \iff f(n) = O(g(n)) \wedge f(n) = \Omega(g(n))\)

    \[\begin{align*} f(n) = \Theta(g(n)) &\iff \exists c_1, c_2,N>0, \forall n \ge N, \text{有 } 0 \le c_1 g(n) \le f(n) \le c_2 g(n), \\ f(n) = \Omega(f(n)) &\iff \exists c_1,N>0, \forall n \ge N, \text{有 } 0 \le c_1 g(n) \le f(n), \\ f(n) = O(g(n)) &\iff \exists c_2,N>0, \forall n \ge N, \text{有 } 0 \le f(n) \le c_2 g(n), \\ \end{align*} \]

    对照即可

  • 证明：\(o(g(n)) \cap \omega(g(n)) = \varnothing\)

    \[o(g(n)) \cap \omega(g(n)) = \{ f(n): \forall c,N>0, \exists n \ge N, \text{有 } 0 \le cg(n) < f(n) \lt c g(n) \} = \varnothing \]

  • 给出有两个参数的记号

    \[\begin{align*} \Theta(g(n,m)) &= \{ f(n,m): \exists c_1, c_2,N,M(n \ge N \vee m \ge M \to 0 \le c_1g(n,m) \le f(n,m) \le c_2g(n,m)) \}, \\ O(g(n,m)) &= \{ f(n,m): \exists c,N,M(n \ge N \vee m \ge M \to 0 \le f(n,m) \le cg(n,m)) \}, \\ \Omega(g(n,m)) &= \{ f(n,m): \exists c,N,M(n \ge N \vee m \ge M \to 0 \le cg(n,m)) \le f(n,m) \}. \\ \end{align*} \]

  • 证明：\(a^{\log_bc} = c^{\log_ba}\)

    \[a^{\log_bc} = b^{\log_ba \cdot \log_bc} = c^{\log_ba}. \]

  • 证明：\(\lg(n!) = \Theta(n\lg n)\)

    \[\begin{align*} \lg(n!) &\le n\lg n = \lg n^n , \\ \lg(n!) &= \sum_{k=0}^{n}{\lg k}\\ &\ge \sum_{k=\lceil n/2 \rceil}^{n}{\lg k}\\ &\ge \frac n2\lg{\frac n2} \\ &= \frac n2\lg n - \frac n2 \lg2 \\ &\ge \frac n2\lg n - \frac n4 \lg n, \text{when }n \ge 4 \\ &=\frac 14n \lg n. \end{align*} \]

  • 证明：\(F_i = \frac{\phi^i-\hat\phi^i}{\sqrt5}\)$，其中 $$\phi = \frac{1+\sqrt5}{2}, \hat\phi = \frac{1-\sqrt5}{2}$

    \[\begin{align*} &F_0 = 0, F_1 = 1. \\ \text{if }&F_{i-1} = \frac{\phi^{i-1}-\hat\phi^{i-1}}{\sqrt5}, F_i = \frac{\phi^i-\hat\phi^i}{\sqrt5}, \\ \text{then } &F_{i+1} = F_{i-1} + F_i = \frac{\phi^{i-1}(\phi+1)-\hat\phi^{i-1}(\hat\phi+1)}{\sqrt5} = \frac{\phi^{i+1}-\hat\phi^{i+1}}{\sqrt5}. \\ \end{align*} \]

  • 证明：\(k \ln k = \Theta(n) \implies k = \Theta(n/\ln n)\)

    \[\begin{align*} & k \ln k = \Theta(n) \\\implies & n = \Theta(k \ln k) \\\implies & \ln n = \Theta(ln(k \ln k)) = \Theta(\ln k + \ln\ln k) =\Theta(\ln k) \\\implies & \frac{n}{\ln n} = \frac{\Theta(k \ln k)}{\Theta(\ln k)} = \Theta(\frac{k \ln k}{\ln k}) = \Theta(k) \\\implies & k = \Theta(\frac{n}{\ln n}) \end{align*} \]

  • 证明：\(\lg^*(\lg n) > \lg(\lg^*n), \text{when } n \ne 1\)

    \[\begin{align*} \lg^*n = \min\{ i \ge 0: \lg^{(i)}n \le 1 \} &\implies \lg^*n - 1 = \min\{ i \ge 0: \lg^{(i+1)}n = \lg^{(i)}(\lg n) \le 1 \} = \lg^*(\lg n), \\[2em] x - 1 \ge \lg x &\implies \lg^*(\lg n) = \lg^*n - 1 \ge \lg(\lg^*n) \end{align*} \]

思考题

  • 渐进增长的性质

    \[\begin{align*} & \begin{cases} f(n) = O(g(n)) \\ \lg{g(n)} \ge 1 \\ f(n) \ge 1 \\ \end{cases} \\\implies & \exists c,N>0, \forall n \ge N[0 \le f(n) \le c g(n)] \\\implies & \lg f(n) \le \lg(c g(n)) = \lg c + \lg g(n) \\\implies & \lg f(n) = O(\lg g(n)) \\ \end{align*} \]

    \[\begin{align*} g(n) = o(f(n)) \implies& \forall c \ge 0, \exists N > 0, \forall n \ge N, 0 \le g(n) \le cf(n) \\\implies& \forall c \ge 0, \exists N > 0, \forall n \ge N, 0 \le f(n) \le f(n) + g(n) \le (1+c)f(n) \\\implies& f(n) + o(f(n)) = \Theta(f(n)). \end{align*} \]

  • \(\overset{\infty}{\Omega}(g(n)) = \{ f(n): \exists c,\text{对无穷多个整数 }n, 0 \le cg(n) \le f(n) \}\)

    证明：\(\forall f,g\in\text{渐进非负函数}[f(n) = O(g(n)) \vee f(n) = \overset{\infty}{\Omega}(g(n))] = \bf T\)\(，\)\(\forall f,g[f(n) = O(g(n)) \wedge f(n) = \Omega(g(n))] = \bf F\)

    \[\begin{align*} \neg[f(n) = O(g(n))] &= \neg[\exists c,N>0, \forall n \ge N(0 \le f(n) \le c g(n))] \\ &= \forall c,N>0, \exists n \ge N[cg(n) < f(n)], \\[2em] &\text{不妨依次取 } n = n_i, N_i = n_i, (i < j \implies n_i < n_j), \\ &\text{则显然 }\forall N \text{ 意味着 $n$ 有无穷个, 这与 $\overset{\infty}{\Omega}(g(n))$ 定义相合} \\ &\text{即 }\neg[f(n) = O(g(n))] \to f(n) = \overset{\infty}{\Omega}(g(n)), \\ &\text{由 }\neg p \to q \equiv p \vee q \text{ 得证}. \end{align*} \]

分治策略

递归求解问题的步骤

  • 分解
  • 解决
  • 合并

求解递归式的方法

  • 代入法：猜测和代入求解。

  • 递归树法：模拟递归调用的过程画出递归树，观察树的结点（子过程代价）和高度（递归深度），将所有深度的代价相加得到总的代价。但这个总的代价并不总是很精确，需要使用代入法进行更严格的证明。

  • 主方法

    对形如 \(T(n) = aT({n/b}) + f(n)\)$ 的函数（其中 $$n/b$$ 可做 $$\lceil{n/b}\rceil,\lfloor{n/b}\rfloor$ 理解），\(T(n)\) 有如下渐进界

    • \(\text{if }\exists \epsilon>0[f(n) = O(n^{\log_ba-\epsilon})],\text{then }T(n)=\Theta(n^{\log_ba})\)
    • \(f(n)=\Theta(n^{\log_ba})\implies T(n) = \Theta(n^{\log_ba}\lg n)\)
    • \(\text{if }\exists \epsilon>0,c<1,N>0,\forall n\ge N[f(n) = \Omega(n^{\log_ba+\epsilon}) \wedge af(n/b) \le cf(n)], \text{then } T(n)=\Theta(f(n))\)

  • 总结

    特定式子使用主方法，其他使用递归树，最后使用代入法验证。

    有时候不能求出绝对的上下界，只能接近。

练习

  • 修改最大子数组算法，允许其结果为空数组，和为 0

    if low == high:
    return low, high, A[low]
# 改为
if low == high:
    return low, high, max(A[low], 0)

  • 最大子数组的线性算法

    保持两个 \(sum\)，一个为 \(A[1..j]\) 最大子数组 \(maxSum\)，另一个为包含 \(A[j]\) 的最大子数组 \(currSum\)。

    算法要考虑当 \(A[1..j]\) 拓展到 \(A[1..j+1]\) 的情况

    • 因为 \(currSum\) 必须包含 \(A[j+1]\) 或一个一不包含，\(currSum = \max(currSum + A[j+1], 0)\)
    • \(maxSum = \max(maxSum, currSum)\)
    def find_maximum_subarray(A: list):
    max_sum = float('-inf')
    curr_sum = 0
    curr_left = 0
    left, right = 0, 0
    for i, a in enumerate(A):
        curr_sum += a
        if curr_sum > max_sum:
            max_sum = curr_sum
            left = curr_left
            right = i
        if curr_sum < 0:
            curr_sum = 0
            curr_left = i + 1
     return left, right, max_sum

  • \(Strassen\) 算法的代码

    \[\begin{align*} A = \begin{bmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{bmatrix}, B = \begin{bmatrix} B_{11} & B_{12} \\ B_{21} & B_{22} \end{bmatrix}, C = \begin{bmatrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{bmatrix}, \\ C = A \cdot B \implies \begin{bmatrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{bmatrix} = \begin{bmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{bmatrix} \cdot \begin{bmatrix} B_{11} & B_{12} \\ B_{21} & B_{22} \end{bmatrix}. \end{align*} \]

    根据 \(Strassen\) 算法的公式

    def square_matrix_multiply_strassen(A, B):
    if A.shape == (1, 1):
        return array([A[0,0] * B[0,0]])
    
    C = empty_like(A)
    A11, A12, A21, A22 = partition(A)
    B11, B12, B21, B22 = partition(B)
    C11, C12, C21, C22 = partition(C)
    
    S1 = B12 − B22
    S2 = A11 + A12
    S3 = A21 + A22
    S4 = B21 − B11
    S5 = A11 + A22
    S6 = B11 + B22
    S7 = A12 − A22
    S8 = B21 + B22
    S9 = A11 − A21
    S10 = B11 + B12

    P1 = square_matrix_multiply_strassen(A11, S1)
    P2 = square_matrix_multiply_strassen(S2, B22)
    P3 = square_matrix_multiply_strassen(S3, B11)
    P4 = square_matrix_multiply_strassen(A22, S4)
    P5 = square_matrix_multiply_strassen(S5, S6)
    P6 = square_matrix_multiply_strassen(S7, S8)
    P7 = square_matrix_multiply_strassen(S9, S10)

    C11 = P4 + P5 + P6 − P2
    C12 = P1 + P2
    C21 = P3 + P4
    C22 = P1 + P5 − P3 − P7

    return C

  • 使 \(Strassen\) 算法适应矩阵规模不为 2 的幂的情况，并证明算法运行时间为 \(\Theta(n^{\lg7})\)

    注意到

    \[\begin{align*} \begin{bmatrix} A & 0 \\ 0 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} B & 0 \\ 0 & 0 \\ \end{bmatrix} = \begin{bmatrix} C & 0 \\ 0 & 0 \\ \end{bmatrix}. \end{align*} \]

    在矩阵周围补全 0 即可

    \[\begin{align*} \text{assert } & 2^k < n < 2^{k+1} \\ T(n) &= T(2^{k+1}) \\ &= \Theta(2^{(k+1)\cdot\lg7}) \\ &\xlongequal{2n > 2^{k+1}} \Theta(n^{\lg7}) = \Theta(2^{(k+1)\cdot\lg7}) = \Theta((2n)^{\lg7}) = \Theta(7n^{\lg7}). \end{align*} \]

  • k 次乘法完成 \(3 \times 3\) 矩阵相乘，求最大 k 使得 \(T(n) = o(n^{\lg7})\)

    \[\begin{align*} T = \begin{cases} k & n \le 3 \\ kT(n/3) + \Theta(n^2) & n > 3 \end{cases} &\implies T(n) = \Theta(k^{\log_3n}) = \Theta(n^{\log_3k}) \\ n^{\log_3k} < n^{\lg7} \implies \log_3k < \lg7 &\implies k < 7^{\lg3} \approx 21.849862224905138 \\ k &= 21 \end{align*} \]

  • \((kn \times n) \cdot (n \times kn)\)

    \[\begin{align*} A = \begin{bmatrix} A_1 \\ A_2 \\ \vdots \\ A_k \end{bmatrix}, B = \begin{bmatrix} B_1 & B_2 & \cdots & B_k \end{bmatrix}, \\ A \cdot B = \begin{bmatrix} A_1B_1 & A_1B_2 & \cdots & A_1B_k \\ A_2B_1 & A_2B_2 & \cdots & A_2B_k \\ \vdots & \vdots & \ddots & \vdots \\ A_kB_1 & A_kB_2 & \cdots & A_kB_k \\ \end{bmatrix}, \\[2em] T(n) = k^2 \Theta(n^{\lg7}) = \Theta(k^2n^{\lg7}). \end{align*} \]

  • \((n \times kn) \cdot (kn \times n)\)

    \[\begin{align*} B \cdot A &= \sum_{i=1}^kA_iB_i, \\ T(n) &= k \Theta(n^{\lg7}) = \Theta(kn^{\lg7}). \end{align*} \]

  • 三次乘法实现复数相乘

    \[\begin{align*} &\ (a+bi) \cdot (c+di) \\ =&\ a(c+di) + b(-d+ci) \\ =&\ \begin{cases} a(c+d) + a(-d+di) - bd + bci = \underbrace{[a(c+d)-d(a+b)]}_R + (ad+bc)i \\ a(c+d)i + a(c-ci) - bd + bci = (ac - bd) + \underbrace{[a(c+d)+c(-a+b)]}_Zi \\ \end{cases} \\ =&\ (ac-bd) + (bc+ad)i,\\[2em] &\ R = ac - bd = a(c+d) - d(a+b), \\ &\ Z = bc + ad = a(c+d) + c(-a+b), \\ \text{let }& P_1 = a(c+d), P_2 = d(a+b), P_3 = c(b-a), \\ \text{then }& R = P_1 - P_2, Z = P_1 + P_3. \end{align*} \]

  • 证明 \(T(n) = 2T(\lfloor{n/2}\rfloor+17)+n \implies T(n) = O(n\lg n)\)

    \[\begin{align*} T(n) &\le 2c(\lfloor{n/2}\rfloor+17)\lg{(\lfloor{n/2}\rfloor+17)}+n \\ &\le c(n+34)\lg(\lfloor{n/2}\rfloor+17) + n \\ &\le c(n+34)\lg(\lfloor{n/1.5}\rfloor) + n, \text{ when } n \ge 103 \\ &= cn\lg n + 34c\lg(\lfloor{n/1.5}\rfloor) - cn\lg1.5 + n \\ &\le cn\lg n, \text{ when } c > C_0. \\ 34C_0\lg(\lfloor{n/1.5}\rfloor) &- C_0n\lg1.5 + n \le 0 \implies C_0 \ge \frac{1}{\lg1.5 - \lg(\lfloor{n/1.5}\rfloor)/n}, \\ \text{pick } n \ge 1000 \text{ and } &C_0 \ge 2 , \text{then } 2 > 1.737 > \frac{1}{\lg1.5 - \lg(\lfloor{1000/1.5}\rfloor)/1000}. \end{align*} \]

    减去一个低阶项，采用更近的上界来简化证明：\(T(n) \le c(n-34)\lg(n-34)\)

    \[\begin{align*} T(n) &= 2T(\lfloor{n/2}\rfloor+17)+n \\ &= 2c(\lfloor{n/2}\rfloor+17-34)\lg(\lfloor{n/2}\rfloor+17-34) + n \\ &\le c(n-34)\lg(n/2-17) + n \\ &= c(n-34)\lg(n-34) - c(n-34)\lg2 + n \\ &= c(n-34)\lg(n-34) - (c-1)n + 34c \\ &\le c(n-34)\lg(n-34), \text{ when } (c-1)n - 34c \ge 0, \\ &\text{pick }c = 2, n \ge 68. \end{align*} \]

  • 证明：\(T(n) = T(n-1) + n \implies T(n) = O(n^2)\)

    \[\begin{align*} T(n) &= c(n-1)^2 + n \\ &= cn^2 - (2c-1)n + c \\ &\le cn^2, \text{ when } c \ge 1. \end{align*} \]

  • 证明：\(T(n) = T(\lceil{n/2}\rceil)+1 \implies T(n) = O(\lg n)\)

    \[\begin{align*} \text{减去低阶项，证明 } T(n) &= O(\lg(n-2)), \\ T(n) &= c\lg(\lceil{n/2}\rceil-2) + 1 \\ &\le c\lg(n/2-1) + 1 \\ &= c\lg(n-2) - c\lg2 + 1 \\ &\le c\lg(n-2), \text{ when } c \ge 1. \end{align*} \]

  • 证明：\(T(n) = 2T(\lfloor{n/2}\rfloor)+n \implies T(n) = \Omega(n\lg n)\)

    \[\begin{align*} \text{加上低阶项，证明 } T(n) &= \Omega((n+2)\lg(n+2)), \\ T(n) &\ge 2c(\lfloor{n/2}\rfloor+2)\lg(\lfloor{n/2}\rfloor+2) + n \\ &\ge 2c(n/2+1)\lg(n/2+1) + n \\ &= c(n+2)\lg((n+2)/2) + n \\ &= c(n+2)\lg(n+2) - c(n+2)\lg2 - n \\ &= c(n+2)\lg(n+2) + ((1-c)n - 2c) \\ &\ge c(n+2)\lg(n+2), \text{ when } 0 \le c < 1, n \ge \frac{2c}{1-c}. \end{align*} \]

  • 证明：归并排序的严格递归式的解为 \(\Theta(n\lg n)\)

    \[T(n)= \begin{cases} \Theta(1) & \text{if } n=1 \\ T(\lceil{n/2}\rceil)+T(\lfloor{n/2}\rfloor)+\Theta(n) & \text{if } n>1 \end{cases}. \]

    \[\begin{align*} \text{证 }T(n) &= O((n-2)\lg(n-2)), \\ T(n) &= c(\lceil{n/2}\rceil-2)\lg(\lceil{n/2}\rceil-2) + c(\lfloor{n/2}\rfloor-2)\lg(\lfloor{n/2}\rfloor-2) + \Theta(n) \\ &\le 2c(\lceil{n/2}\rceil-2)\lg(\lceil{n/2}\rceil-2) + \Theta(n) \\ &\le c(n-2)\lg(n/2-1) + \Theta(n) \\ &= c(n-2)\lg(n-2) - c(n-2)\lg2 + kn \\ &= c(n-2)\lg(n-2) - (c-k)n + 2c \\ &\le c(n-2)\lg(n-2), \text{ when } c > k, n \ge \frac{2c}{c-k}. \\ \text{证 }T(n) &= \Omega((n+2)\lg(n+2)), \\ T(n) &= c(\lceil{n/2}\rceil+2)\lg(\lceil{n/2}\rceil+2) + c(\lfloor{n/2}\rfloor+2)\lg(\lfloor{n/2}\rfloor+2) + \Theta(n) \\ &\ge 2c(\lfloor{n/2}\rfloor+2)\lg(\lfloor{n/2}\rfloor+2) + \Theta(n) \\ &\ge c(n+2)\lg(n/2+1) + \Theta(n) \\ &= c(n+2)\lg(n+2) - c(n+2)\lg2 + kn \\ &= c(n+2)\lg(n+2) + (k-c)n - 2c \\ &\ge c(n-2)\lg(n-2), \text{ when } 0 \le c < k, n \ge \frac{2c}{k-c}. \end{align*} \]

    注意两个证明中的 \(c\) 不同。

  • 使用代入法减去低阶项，证明：\(T(n) = 4T(n/3) + n \implies T(n) = \Theta(n^{\log_34})\)

    \[\begin{align*} T(n) &= 4T(n/3) + n \\ &\le 4c{(\frac n3)}^{\log_34} + n \\ &= cn^{\log_34} + n, \text{ 无法得证,} \\ \text{注意到上式有 $n$ 项，试证 } T(n) &= cn^{\log_34} - dn \\ T(n) &\le 4c{(\frac n3)}^{\log_34} - \frac 43dn + n \\ &= cn^{\log_34} - (\frac 43d-1)n \\ &\le cn^{\log_34}, \text{ when } d \ge \frac 34. \end{align*} \]

  • 求解 \(T(n) = 3T(\sqrt n)+\lg n\)

    \[\begin{align*} \text{let } S(m) &= T(2^m), \\ S(m) &= T(2^m) = 3T(2^{m/2}) + m \\ &= 3S(m/2) + m \\ &\xlongequal{\text{guess } S(m) = O(cm^{\lg3} - dm)} 3O(c(\frac m2)^{\lg3}-\frac d3m) + m \\ &\le 3c(\frac m2)^{\lg3} - dm + m \\ &= cm^{\lg3} - (d-1)m \\ &\le cm^{\lg3}, \text{ when } d \ge 1, \\ S(m) &= O(m^{\lg3}) \implies T(n) = O(\lg^{\lg3}n). \end{align*} \]

  • 求解：\(T(n)=T(n/2)+n^2\)

    \[\begin{align*} T(n) &= \sum_{i=0}^{\lg n} \frac{cn^2}{4^i} \\ &< \sum_{i=0}^{\infty} \frac{cn^2}{4^i} \\ &= \frac{1-(1/4)^{\infty}}{1-1/4}cn^2 \\ &= \frac 43cn^2\\ &= O(n^2), \\[2em] T(n) &\le c(\frac n2)^2 + n^2 \\ &= (1+c/4)n^2 \\ &\le cn^2, \text{ when } c \ge \frac43. \end{align*} \]

  • 求解：\(T(n) = 4T(n/2+2)+n\)

    将 \(T(n/2+2)\) 看做 \(T(n/2)\) 求递归树

    对递归树，深度为 \(\lg n\)，第 \(i\) 层有 \(4^i\) 个结点，每个结点的代价为 \(n/2^i\)

    \[\begin{align*} T(n) &= 4T(n/2) + n \\ &= \sum_{i=0}^{\lg n}4^i{cn \over 2^i} \\ &= {1-2^{\lg n} \over 1-2} cn \\ &= cn^2-cn \\[2em] T(n) &= 4T(n/2+2) + n \\ &\xlongequal{T(n)=cn^2-dn} 4(c(\frac n2+2)^2 - d(\frac n2+2)) + n \\ &= cn^2 - dn + (8c-d+1)n + 16c - 8d \\ &\le cn^2 - dn, \text{ when } 8c-d+1 < 0, n \ge {16c-8d \over 8c-d+1} \end{align*} \]

  • 使用递归树求解 \(T(n) = T(n-a) + T(a) + cn\)

    \[\begin{align*} \text{let } T(a) &= A \\ T(n) &= T(n-a) + A + cn \\ &= \sum_{i=0}^{n/a}c(n-ia+2A) \\ &= \frac can^2 - {ca\over2}(\frac na)^2 + 2cA\frac na \\ &= {c \over 2a}n^2 + {2cA \over a}n \\ &= O(n^2) \end{align*} \]

  • 使用递归树求解 \(T(n) = T(\alpha n)+T((1-\alpha)n)+cn\)

    当 \(\alpha \ne 1/2\) 时，递归树是不平衡的，路径长度为 \(-\log_{\alpha}n\) 和 \(-\log_{1-\alpha}n\)，猜测上界为 \(O(n\lg n)\)

    \[\begin{align*} T(n) &= d(\alpha n)\lg(\alpha n) + d((1-\alpha)n)\lg((1-\alpha)n) + cn \\ &= \alpha dn\lg n + \alpha dn\lg\alpha + (1-\alpha)dn\lg n + (1-\alpha)dn\lg(1-\alpha) + cn \\ &= dn\lg n + dn[\alpha\lg\alpha + (1-\alpha)\lg(1-\alpha)] + cn \\ &\le dn\lg n,\text{ when } d \ge -{c\over\alpha\lg\alpha + (1-\alpha)\lg(1-\alpha)} \end{align*} \]

思考题

  • 参数传递代价，归并排序

    \[\begin{align*} T_{pass}&=\Theta(1)& T(n)&=2T(n/2)+2\Theta(1)+\Theta(n)=\Theta(n\lg n) \\ T_{pass}&=\Theta(N)& T(n)&=2T(n/2)+2\Theta(N)+\Theta(n)=\Theta(n\lg n)+\Theta(N^2) \\ T_{pass}&=\Theta(q-p+1)& T(n)&=2T(n/2)+2\Theta(n/2)+\Theta(n)=\Theta(n\lg n) \\ \end{align*} \]

  • 斐波那契数，\(\mathcal F(z)=\sum_{i=0}^\infty F_iz^i\)

    \[\begin{align*} \mathcal F(z)&=z+z\mathcal F(z)+z^2\mathcal F(z) \\ \mathcal F(z)&={z\over1-z-z^2}=\frac1{\sqrt5}(\frac1{1-\phi z}-\frac1{1-\hat\phi z}) \\ &\xlongequal{\text{taylor expansion}}\sum_{i=1}^\infty\frac1{\sqrt5}(\phi^i-\hat\phi^i)z^i \end{align*} \]

  • 更多递归式

    对形如 \(T(n) = aT({n/b}) + f(n)\) 的函数（其中 \(n/b\) 可做 \(\lceil{n/b}\rceil,\lfloor{n/b}\rfloor\) 理解），\(T(n)\) 有如下渐进界

    • \(\text{if }\exists \epsilon>0[f(n) = O(n^{\log_ba-\epsilon})],\text{then }T(n)=\Theta(n^{\log_ba})\)
    • \(f(n)=\Theta(n^{\log_ba})\implies T(n) = \Theta(n^{\log_ba}\lg n)\)
    • \(\text{if }\exists \epsilon>0,c<1,N>0,\forall n\ge N[f(n) = \Omega(n^{\log_ba+\epsilon}) \wedge af(n/b) \le cf(n)], \text{then } T(n)=\Theta(f(n))\)

    \[\begin{align*} a.T(n)&=4T(n/3)+n\lg n=\Theta(n^{\log_34}) \\ b.T(n)&=3T(n/3)+n/\lg n=\Theta(n) \\ c.T(n)&=4T(n/2)+n^{2.5}=\Theta(n^{2.5}) \\ d.T(n)&=3T(n/3-2)+n/2=\Theta(n\lg n) \\ e.T(n)&=2T(n/2)+n/\lg n=\Theta(n) \\ f.T(n)&=T(n/2)+T(n/4)+T(n/8)+n,\text{使用代入法}\\&\xlongequal{比较宽的上界,n>C_{常数}}O(n\lg n)\\&\xlongequal{比较窄的上界,c>C_{常数}}O(cn) \\ g.T(n)&=T(n-1)+1/n=\sum_{i=1}^n1/i\xlongequal{\text{调和级数前 n 项和}}\psi(n+1)+\gamma\\&\approx\lg n+\frac1{2n}=\Theta(\lg n)\\ h.T(n)&=T(n-1)+\lg n=\sum_{i=1}^n\lg i=\int\sum_{i=1}^n1/i\approx n\lg n-n+\frac12\lg n=\Theta(n\lg n) \\ i.T(n)&=T(n-2)+1/\lg n=\Theta(n/\lg n) \\ j.T(n)&=\sqrt nT(\sqrt n)+n\\&\xlongequal{n=2^{2^m}}2^{2^{m-1}}T(2^{2^{m-1}})+2^{2^{m}}\\&\xlongequal{S(m)=T(2^{2^m})}2^{2^{m-1}}S(m-1)+2^{2^m}\\&=\sum_{i=1}^m2^{2^i}=\Theta(m2^{2^m})\\&=\Theta(n\lg(\lg n)) \end{align*} \]

    \[\begin{align*}\begin{array}{l} f\ 可用\ Akra\text-Bazzi\ 方法: \\[1em] (1/2)^p+(1/4)^p+(1/8)^p=1, \\[1em] q=\root3\of{3\sqrt{33}+19}, p=\log\left(\frac13+\frac4{3q}+\frac{q}3\right)/\log2\approx0.88, \\[1em] T(n)=\Theta(n^p(1+\int^n_1x^{-p}\mathrm{d}x))=\Theta({n-pn^p\over1-p}). \end{array}\end{align*} \]

    得到这个值与之前方法得到的上界的比值曲线，横轴为 \(n\)，纵轴为 \(n\lg n/T(n),cn/T(n)\)。

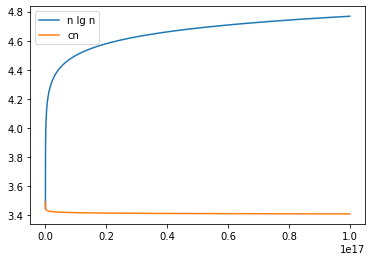
  • 挑芯片

    超过 \(n/2\) 块芯片是好的，寻找一块好芯片

    1. 将所有芯片分为 \(\lfloor n/2\rfloor\) 组，每组 \(2\) 个；
    2. 设检测后有 \(m\) 组显示两者都为好，则 \(m\ge1\) 且至少有一半以上是两个都是真的好的；
    3. 选择这 \(m\) 组中的任意一半成为子问题。

    \(T(n)=T(m)+\lfloor n/2\rfloor\le T(n/2)+n/2,T(n)\le\Theta(\lg n)\)

  • Monge 阵列

    \[\begin{align*}\begin{array}{} \begin{array}{} 证明:Monge(A)\iff&\forall i\in[1..m-1],\forall j\in[1..n-1] \\ &(A[i,j]+A[i+1,j+1]\le A[i,j+1]+A[i+1,j]) \\ \end{array} \\ (\Rightarrow)\ 定义 \\ (\Leftarrow)\text{ let $k=i+x,l=j+y$,}\\ \qquad\text{then }A[i,j]-A[i,j+1]\le A[i+1,j]-A[i+1,j+1], \\ \qquad\qquad\ A[i,j+1]-A[i,j+2]\le A[i+1,j+1]-A[i+1,j+2], \\ \qquad\qquad\ \dots \\ \qquad 相加得\ A[i,j]-A[i,l]\le A[i+1,j]-A[i+1,l] \\ \qquad k\ 同理 \ A[i,j]-A[i,l]\le A[k,j]-A[k,l] \end{array}\end{align*} \]

    \(f(i)\) 为第 \(i\) 行最左边的最小元素得列下标，证明：\(f(1)\le f(2)\le\cdots\le f(m)\)

    \[\begin{align*} 证明:&f(i)\le f(i+1) \\ 反证法:&\text{let $a=f(i),b=f(i+1),a>b$,}\\ &\text{then $A[i,b]+A[i+1,a]\le A[i,a]+A[i+1,b]$}, \\ &\qquad\ \because A[i+1,b]\le A[i+1,a],\therefore A[i,a]\ge A[i,b] \\ &\qquad\ f(i)=a\to A[i,a]<A[i,b],contradictory \end{align*} \]

    在偶数行最左最小元素已知的情况下在 \(O(m+n)\) 时间内得到奇数行最左最小元素。

    偶数行最小元素将矩阵划分为 \([0,f(2)],[f(2),f(4)],\dots,[f(2\lfloor (m-1)/2\rfloor),n-1]\) 区间，在这些区间内寻找奇数行最左最小元素，最后一个区间需不需要寻找取决于 m 是偶数还是奇数。时间为扫描每个区间的时间的和：\(m/2+n\)。

    \[\begin{align*} T(m,n)=\begin{cases} O(n), & m=1, \\ \overbrace{T(\lceil m/2\rceil,n)}^\text{even lines}+\overbrace{O(\lfloor m/2\rfloor+n)}^\text{odd lines}, &m\ne1, \\ \end{cases} \\[1em] 使用递归树方法,T(n)=O(m+n\lg m) \end{align*} \]

概论分析和随机算法

当概率分布在算法的输入上时，讨论平均情况运行时间；当算法本身作出随机选择（使用随机数生成器）时，讨论期望运行时间。由于算法中做出了随机选择，后者对同样的输入可能产生不同的运行时间和运行结果。因为运行环境只会提供伪随机数生成器，所以算法的输入不包括伪随机数生成器的输入。

def f1(array):
    """平均情况运行时间"""
    return merge_sort(array)
def f2(array):
    """期望运行时间"""
    shuffle(array)
    return merge_sort(array)

指示器随机变量 \(I\{A\}=\begin{cases}1&\text{如果 }A\text{ 发生}\\0&\text{如果 }A\text{ 不发生}\end{cases},E[X_A]=E[I\{A\}]=Pr\{A\}\)

随机排列数组的方法：

def permute_by_sorting(array):
    RANDOM_PERMUTE_C = 50
    n = len(array)
    p = [randrange(len(array) ** RANDOM_PERMUTE_C) for _ in range(n)]
    # return [array[i] for i in sorted(list(range(n)), key=p.__getitem__)]
    return list(map(array.__getitem__, sorted(list(range(n)), key=p.__getitem__)))

def ranomize_by_swap(array):
    array = array[:]
    for i in range(len(array)):
        j = randrange(i, len(array))
        array[i], array[j] = array[j], array[i]
    return array

RANDOM_PERMUTE_C 越大则 p 中的优先级越唯一，排序结果越均匀。

把球投到箱子里（用于分析散列的模型）的问题。平均投多少个球才能使每个箱子中有一个球：

\[\begin{align*} &\text{设箱子 $b$ 个，平均投球 $n$ 个；}\\ &\text{设在前 $i-1$ 个箱子中有球的情况下使第 $i$ 个箱子中有球的投球次数为随机变量 $n_i$。}\\ &\text{在前 $i-1$ 次时投到第 $i$ 个箱子的概率为 $\frac{b-i+1}b$, $n_i$ 服从关于 $i$ 的几何分布}\\[1em] E[n_i]&={b\over b-i+1},\qquad n=\sum_{i=1}^{b} n_i,\\ E[n]&=\sum_{i=1}^bE[n_i]=\sum_{i=1}^b{b\over b-i+1}\\ &\xlongequal{i\leftarrow b-i+1}\sum_{i=1}^b \frac bi\\ &\xlongequal{调和级数前\ b\ 项和}b(\ln b+\frac1{2b})\\ &=b\ln b+O(1) \end{align*} \]

期望特征序列长度的界（抛硬币 \(n\) 次所得的最长正面期望长度）：

\(L\) 为最长序列长度，\(L_i\) 为该长度为 \(i\) 的事件。注意到 \(i,Pr\lbrace L_i\rbrace\) 呈负相关，当 \(i\) 较小时 \(Pr\lbrace L_i\rbrace\) 较大；反之亦然。

\[\begin{align*} E[L]&=\sum_{i=0}^{n}i\cdot Pr\lbrace L_i\rbrace\\ &=\sum_{i=0}^{2\lceil\lg n\rceil-1}i\cdot Pr\lbrace L_i\rbrace+\sum_{i=2\lceil\lg n\rceil}^ni\cdot Pr\lbrace L_i\rbrace\\ &<2\lceil\lg n\rceil\sum_{i=0}^{2\lceil\lg n\rceil-1}Pr\lbrace L_i\rbrace+n\sum_{i=2\lceil\lg n\rceil}^nPr\lbrace L_i\rbrace\\ &\xlongequal{\sum_{i=0}^{2\lceil\lg n\rceil-1}Pr\lbrace L_i\rbrace<1,\quad\sum_{i=2\lceil\lg n\rceil}^nPr\lbrace L_i\rbrace<1/n}\\ &<2\lceil\lg n\rceil+1=O(\lg n)\\ E[L]&=\sum_{i=0}^{n}i\cdot Pr\lbrace L_i\rbrace\\ &=\sum_{i=0}^{\lfloor(\lg n)/2\rfloor-1}i\cdot Pr\lbrace L_i\rbrace+\sum_{i=\lfloor(\lg n)/2\rfloor}^ni\cdot Pr\lbrace L_i\rbrace\\ &\ge\sum_{i=0}^{\lfloor(\lg n)/2\rfloor-1}0\cdot Pr\lbrace L_i\rbrace+\sum_{i=\lfloor(\lg n)/2\rfloor}^n\lfloor(\lg n)/2\rfloor\cdot Pr\lbrace L_i\rbrace\\ &\xlongequal{\sum_{i=\lfloor(\lg n)/2\rfloor}^nPr\lbrace L_i\rbrace\ge1-O(1/n)}\\ &\ge\lfloor(\lg n)/2\rfloor(1-O(1/n))=\Omega(\lg n) \end{align*} \]

使用 Python 验证特征序列长度的界

import numpy as np
import matplotlib.pyplot as plt

def get_max_count(size, repeat_times=10):
    """返回最大特征序列长度的平均值"""
    while True:
        if repeat_times == 0:
            return None, 0
        try:
            zero = np.zeros((repeat_times, 1), dtype=np.int8)
            sequence = np.append(
                np.random.randint(0, 2, (repeat_times, size), dtype=np.int8),
                zero, axis=1) # 获得序列
            diff = np.diff(sequence, prepend=zero, axis=1)

            begin = np.argwhere(diff > 0).astype(np.uint32) # 特征序列起始位置
            end = np.argwhere(diff < 0).astype(np.uint32) # 特征序列结束位置
            
            split = np.unique(begin[:,0], return_index=True)[1][1:] # grouped by row number
            begin_split = np.split(begin[:,1], split)
            end_split = np.split(end[:,1], split)
            
            break
        except MemoryError as err:
            # 内存不足
            print(err)
            repeat_times //= 2

    average = np.sum([np.max(e - b).astype(np.float64)
                      for b, e in zip(begin_split, end_split)])
                / repeat_times
    return average, repeat_times

linspace = np.linspace(8, 30, 150)
sizes = (2 ** linspace).astype(np.int32) 
results = np.zeros_like(sizes, dtype=np.float64)

REPEAT_TIMES = 100
repeat_times = REPEAT_TIMES

for i, size in enumerate(sizes):
    if results[i]:
        continue
    count, repeat_times = get_max_count(size, repeat_times=repeat_times)
    if count is None:
        break
    if repeat_times != REPEAT_TIMES:
        count += sum(get_max_count(size, repeat_times=repeat_times)[0]
                     for _ in range(REPEAT_TIMES // repeat_times))
        count /= REPEAT_TIMES // repeat_times + 1
    results[i] = count
    print(f'results[{i}] {size}: {results[i]} / {1.5 * np.log(size)} = {results[i] / 1.5 / np.log(size)}')

print(np.average(results / np.log(sizes), weights=sizes)) # 1.410515920608434

plt.plot(linspace, 1.410515920608434 * np.log(sizes), label='log')
plt.plot(linspace, results, label='results')
plt.legend()
plt.show()

plt.plot(linspace, results / 1.410515920608434 / np.log(sizes), label='results / log')
plt.legend()
plt.show()

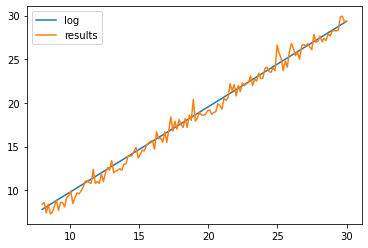
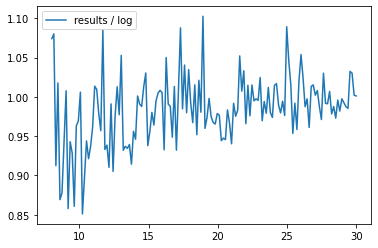
可见 \(E[L]\approx 1.410515920608434\ln n\)

在线雇佣问题：在 \(n\) 应聘者中选择并只选择一个。

拒绝前 \(k\) 个，获得前 \(k\) 个应聘者的最高分，接受之后第一个高于该最高分的应聘者，\(k=n/e\)。

\(S,S_i,B_i,O_i\) 分别为成功得到最高分应聘者、成功得到最高分应聘者且在第 \(i\) 位、最高分应聘者在第 \(i\) 位、前 \(i-1\) 个应聘者被拒绝。

\[\begin{align*} Pr\lbrace S\rbrace&=\sum_{i=k+1}^nPr\lbrace S_i\rbrace\\ &=\sum_{i=k+1}^nPr\lbrace B_i\rbrace Pr\lbrace O_i\rbrace\\ &=\sum_{i=k+1}^n\frac1n\cdot{k\over i-1}\\ &=\frac kn\sum_{i=k}^{n-1}\frac1i\\ &\approx\frac kn(\ln n-\ln k)\\ \end{align*} \]

练习

  • 用 randint(0, 1) 实现 randint(a, b)

    def randint(a, b):
    bitsize = len(bin(b - a)) - 2
    while True:
        bits = (randint(0, 1) for _ in range(bitsize))
        result = a + reduce(lambda x, y: (x << 1) + y, bits)
        if result in range(a, b + 1):
          return result

    \[\begin{align*} T(a,b)&=T(0,1)\times bitsize\times E(loop)\\[1em] &=T(0,1)\times\lceil\lg(b-a)\rceil\times\sum_{i=0}^\infty(i+1)(1-{b-a\over2^{\lceil\lg(b-a)\rceil}})^i{b-a\over2^{\lceil\lg(b-a)\rceil}}\\ &\xlongequal{p={b-a\over2^{\lceil\lg(b-a)\rceil}}}T(0,1)\times\lceil\lg(b-a)\rceil\times p\left(\sum_{i=0}^\infty\left(1-p\right)^{i+1}\right)^\prime\\ &=T(0,1)\times\lceil\lg(b-a)\rceil\times \frac1p\\ &=T(0,1)\times\lceil\lg(b-a)\rceil\times{2^{\lceil\lg(b-a)\rceil}\over b-a}\\ &<T(0,1)\times\lceil\lg(b-a)\rceil\times{2\times 2^{\lg(b-a)}\over b-a}\\[1em] &=T(0,1)\times2\lceil\lg(b-a)\rceil=\Theta(\lg(b-a)) \end{align*} \]

  • 用有偏的 biased_randint(0, 1) 实现无偏的 randint(0, 1)

    def randint(0, 1):
    while (a := biased_randint(0, 1)) == (b := biased_randint(0, 1)):
        pass
    return a

    \(times={1 − 2p(p − 1)\over2p(p − 1)}\)

  • HIRE-ASSISTANT 中雇佣一次的概率和 n 次的概率

    \[\begin{align*} 一次&: a_0 \ge a_i(i>0) & Pr&=\frac1n \\ n次&:a_0<a_1<\cdots<a_i<a_n & Pr&=\frac1{n!} \\ 2次&:将数分为两堆，这两堆分别降序，减去雇佣一次的情况&Pr&={\sum_{k=1}^{n-1}\binom nk-1\over n!}={2^n-n-1\over n!} \end{align*} \]

  • \([1..n]\) 上的均匀随机数列的逆序对个数期望

    \[\begin{align*} &\text{let $f(i,j)$ represent $i<j\wedge A[i]>A[j]$} \\ E&=\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}Pr\{f(i,j)\}\\ &=\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}\frac12\\ &=\frac12\sum_{i=1}^{n-1}n-i\\ &=\frac12\left[n(n-1)-{(n-1)n\over2}\right]\\ &=\frac{n(n-1)}4 \end{align*} \]

  • 产生除恒等排列以外（indentity permuatation）的任意排列

    Kelp 教授的方法不能实现要求，这一算法使得所有数字都离开原位，显然有部分排列不能被生成。

  • PERMUTE-WITH-ALL，\(swap(A[i], A[RANDOM(1,n)])\)

    使用此算法获得的结果有 \(n^n\) 种，全排列有 \(n!\) 个，要获得随即均匀排列，必要条件为两者为整除关系，显然不一定满足。

    \(n^n/n!=\prod_{i=1}^{n-1}n/i\)

  • Armstrong 教授的算法

    def permute_by_cyclic(a):
    n = len(a)
    b = [None for _ in range(n)]
    offset = random.randrange(0, n)
    for i in range(n):
        dest = i + offset
        if dest >= n:
            dest -= n
        b[dest] = a[i]
    return b
# 实际上该算法等同于
def permute_by_cyclic(a):
    offset = random.randrange(0, n)
    b = a[:offset] + a[offset:]

  • [random.randrange(0, n ** 3) for _ in range(n)] 产生的元素都唯一的概率至少为 \(1-1/n\)

    求不唯一的概率为

    \[\begin{align*} Pr\lbrace \exists i,j\in[0..n-1](i\ne j\wedge P[i]=P[j])\rbrace&=Pr\lbrace \bigcup _{i,j\in[0..n-1],i\ne j}P[i]=P[j]\rbrace\\ &\le\sum_{i,j\in[0..n-1],i<j}Pr\lbrace P[i]=P[j]\rbrace\\ &={n(n-1)\over 2n^3}\\ &\le\frac1n \end{align*} \]

  • PERMUTE-BY-SORTING 处理相同优先级

    对具有相同优先级的数再次进行 PERMUTE-BY-SORTING，直到没有相同的优先级。

  • 随机样本

    def random_sample(m, n):
    if m == 0:
        return []
    s = random_sample(m - 1, n - 1)
    i = random.randrange(0, n)
    s.append(n - 1 if i in s else i)
    return s

    证明所有 m 子集是等可能的。

    random_sample(1, n) 成立，因为 i in s 恒为 False；random_sample(n, n) 成立，因为 i in s 恒为 True。

    如果 random_sample(m - 1, n - 1) 产生等可能的 \([0..n-2]\) 的 m-1 子集，则由于 random.randrange(0, n) 产生 \([0..n-1]\) 的任意一个数，\(n-1\) 被添加的概率为

    \[\begin{align*} \underbrace{n-1\over n}_{i\in[0..n-2]}\cdot\underbrace{C_{n-2}^{m-2}\over C_{n-1}^{m-1}}_{i\in random\text-sample(m - 1, n - 1)}+\frac1n=\frac mn \end{align*} \]

    其他数在其中的概率（可能被添加，也可能已经在了）

    \[\begin{align*} \frac1n(1-{m-1\over n-1})+{m-1\over n-1}=\frac mn \end{align*} \]

    因此所有数的概率都为 \(m/n=C^{m-1}_{n-1}/C^m_n\)

  • 生日悖论

    \[\begin{align*} \text{let $my birthday=b$}\\ Pr\lbrace b_i=b\rbrace&=\frac1n\\ Pr\lbrace\exists i\in[1..k](b_i=b)\rbrace&=Pr\lbrace\bigcup_{i\in[1..k]} b_i=b\rbrace\\ &=1-Pr\lbrace\bigcap_{i\in[1..k]} b_i\ne b\rbrace\\ &=1-({n-1\over n})^k\ge\frac12\\ Pr\lbrace\exists i,j\in[1..k],i\ne j(b_i=b_j=\text{"7-4"})\rbrace&=Pr\lbrace\bigcup_{i,j\in[1..k],i\ne j} b_i=b_j=\text{"7-4"}\rbrace\\ &=1-Pr\lbrace\bigcup_{i\in[1..k]} b_i\ne\text{"7-4"}\rbrace-\sum_{i=1}^kPr\lbrace b_i=b\rbrace Pr\lbrace\bigcup_{j\in[1..k],j\ne i} b_i\ne b_j\rbrace\\ &=1-({n-1\over n})^k-k\frac1n({n-1\over n})^{k-1}\\ &=1-{(n+k-1)(n-1)^{k-1}\over n^k}\ge\frac12 \end{align*} \]

  • 投到任一箱子里有两个球的期望

    投入第 \(i\) 个球使仍未成功，说明此时有 \(i\) 个箱子中有球，设次数为 \(n\)

    \[\begin{align*} E[n]&=\sum_{i=2}^{b+1}i\cdot Pr\lbrace n=i\rbrace\\ &=\sum_{i=2}^{b+1}i{i-1\over b}\prod_{i=0}^{i-2}{b-i\over b}\\ \end{align*} \]

  • 分析生日悖论时需要生日彼此独立还是两两独立即可

    两两独立即可，因为使用概率分析时只需要在两两独立的前提下就可以算出生日在同一天上的概率。

  • 3 人生日相同

    \(Pr\lbrace b_i=b_j=b_k=b\rbrace=1/n^3\)

    所求结果为 \(1-Pr\lbrace 两两不同\rbrace-Pr\lbrace 有两两相同没有三三相同\rbrace\)

    \(Pr\lbrace 两两不同\rbrace={n!\over n^n(n-k)!}\)

    \(Pr\lbrace 有两两相同没有三三相同\rbrace=\sum_{i=1}^{\lfloor k/2\rfloor}\left[C_n^i\prod_{j=0}^{i-1}C_{k-2j}^2\cdot\prod_{j=1}^{k-2i}(n-i-j+1)\right]\Large/n^n\)

    使用指示器随机变量分析会比较简单。

  • n 球投入 n 箱，空箱子的期望

    \[\begin{align*} E[empty]&=E[\sum_{i=1}^nI\lbrace nboxes[i].isempty\rbrace]\\ &=\sum_{i=1}^nE[I\lbrace boxes[i].isempty\rbrace]\\ &=\sum_{i=1}^nPr\lbrace boxes[i].isempty\rbrace\\ &=\sum_{i=1}^n(\frac{n-1}n)^n=n(\frac{n-1}n)^n \end{align*} \]

思考题

  • R. Morris 的概率计数法

    考虑一个 \(b\) 位的计数器，里面存储了 \(2^b\) 个递增的数 \(n_0=0,n_1,\dots,n_{2^b-1}\)，技术单元以 \(1/(n_{i+1}-n_i)\) 从 \(n_i\) 自增到 \(n_{i+1}\)。

    a. 如果当前数为 \(n_i\)，进行 \(n_{i+1}-n_i\) 次 INC 操作后，期望为 \(n_{i+1}\)；进行 \(n<n_{i+1}-n_i\) 次 INC 操作之后，期望为 \(n/(n_{i+1}-n_i)\)，期望为 \(n_i+n\)。将多次 INC 操作分为上述两种类别即可。

    b. \(p=0.01\)，每次操作都有概率自增，这是一个二项分布，其成功次数方差为 \(np(1-p)=0.0099n\)。由于 \(n_i=100i\)，表示的数的方差为 \(99n\)。

  • 查找无序数组

    a.

    def search(array, target):
    n = len(array)
    mark = {}
    while len(mark) < n:
        while (index := random.randrange(0, n)) in mark:
            pass
        mark[index] = None
        if array[index] == target:
            return index
    return -1

    b. \(n\)

    c. 几何分布 \(\sum_{i=0}^\infty i({n-k\over n})^{i-1}(k/n)=n/k\)

    d. 使所有箱子都被投入一个球，\(n(\ln n+O(1))\)

    e. \((n+1)/2\)、\(n\)

    f. \((n+1)/(k+1)\)

    g. 都为 \(n\)

    h. 除了打乱操作以外，运行时间相同

posted @ 2022-10-27 20:46  Violeshnv  阅读(73)  评论(0)  编辑  收藏  举报