聚类
聚类
聚类方法在于寻找数据中的集群(clusters),在同一个集群中的数据在某些方面更加相似。这同时也是对数据的一种压缩,因为我们使用了更小的集合—集群—来表示更大的数据。也可以理解为寻找有用特征的一种方式,如果一系列数据可以很好地被集群中心点表示,那么很有可能我们发现了更好的特征。
为了获得聚类算法,我们先要明确数据之间的相似度的概念,一般用数据之间的距离来表示。假设数据分布于特征空间 \(\mathcal X=\mathbb R^D\),那么我们需要一个函数来计算两个数据在该空间的距离,一般使用欧氏距离 \(\vert\vert\pmb x_1-\pmb x_2\vert\vert_2=\sqrt{\sum_{i=1}^D(x_1^{(i)}-x_2^{(i)})^2}\),但对于某些特殊的数据也使用其他距离函数。
K-均值聚类
K-均值聚类是一个迭代算法,简单并且可解释。将所有数据用 k 个类(cluster,或者称为集群)表示,这 k 个集群的中心点用所有属于这个集群的数据的均值表示,这也是为什么它被命名为均值聚类。
推导K-均值算法
设 \(\lbrace{\pmb\mu_i}\rbrace_{i=1}^k\) 为 k 个中心点,\(\lbrace r_i\rbrace_{i=1}^n\) 为 n 个数据属于哪些类,将损失函数设为所有样本与其所属类的中心的欧氏距离之和。
其中 \(I\) 为指示器函数,\(I\lbrace A\rbrace=\begin{cases}1&\text{if }A\\0&\text{else}\end{cases}\)。
使得损失函数 \(J(\lbrace\pmb x_i\rbrace_{i=1}^n;\lbrace\pmb\mu_i\rbrace_{i=1}^n,\lbrace r_i\rbrace_{i=1}^n)\) 获得极小值的结果由很多种,这说明如果使用随机初始化每个样本的集群,那么每次获得的聚类结果都很可能不一样。
实现
-
初始化 k 个不同的中心点 \(\pmb\mu^{(1)},\pmb\mu^{(2)},\dots,\pmb\mu^{(k)}\);
-
重复迭代直到中心点不在变动
- 每个样本分配到最近的中心点 \(\pmb\mu^{(i)}\),表明它属于类 \(i\);
- 每个中心点 \(\pmb\mu^{(i)}\) 被更新为类 \(i\) 中所有样本的均值。
def k_means(a:np.ndarray, k:int, clusters:np.ndarray = None):
"""take an NxD numpy matrix as input"""
n, d = a.shape
if n <= k:
return np.arange(n), a.copy()
if clusters is None:
clusters = np.empty((k, d))
responses = np.random.randint(k, size=(n, ))
while True:
for i in range(k):
choose = responses == i
if choose.any():
clusters[i] = np.average(a[responses == i], axis=0)
new_responses = (
(a.reshape(1, *a.shape).transpose(1, 0, 2) - clusters) ** 2
).sum(axis=-1).argmin(axis=-1)
if (new_responses == responses).all():
break
responses = new_responses
return responses, clusters
选择超参数 k
从压缩的角度上看,k 的选择好比压缩率和保真度之间的权衡(trade-off),更高的 k 对原数据的保留程度更高,但是中心点数目更多。
一种简单的方法是通过采用不同的 k 对数据进行聚类之后,选择两项表现综合结果最好的 k 值。如果你想获得更具有代表性的特征的话,那么建议使用更大的 k,如果想要通过聚类观察数据的话应该使用较小的 k。
通过损失函数的变化率选择最好的 k 值
不断增大 k,直到增大 k 后减少的损失降低到某一阈值以下后选择这个 k。即选择满足损失函数 \(J_k\le J_{k+1}+threshold\)。
通过集群分散度(within-cluster dispersion)选择最好的 k 值
\(D_c\) 为集群 \(c\) 的分散度,是集群中所有样本对的欧氏距离;\(W_k\) 为所有集群的归一化分散度。
系数 2 是因为 \(D_c\) 中所有样本对计算了两次。
这一数值体现了每个集群的离散程度。一般随着 k 的增加这一数值会变小,聚类效果越好这一数值也会减小。
但是为了真正地衡量聚类效果,我们需要比较聚类之前的数据和聚类之后的数据之间的差异,即计算间隙统计(gap statistic)
选择最佳的 \(k^*\) 满足 \(k^*=\underset{k}{\arg\max}\,\mathrm{Gap}_N(k)\)。其中,\(\mathbb E_{\mathrm{null}}\) 为我们寻找的一个空分布(null distribution,或称为参考分布 reference distribution),这个空分布是用来生成参考数据(reference data)用的。空分布的选择就是当数据中实际上并不存在“不同类”时候选择的分布。
换句话说,我们假设数据中有不同的类,比如水仙花数据中有茎叶长度的数据,通过这一数据有可能分出几个类,为了选择最好的类的个数 k,那么将茎和叶的长度分别归一化为均值 0 方差 1 的数据后,选择空分布为标准二元高斯分布 \(\mathcal N(\pmb0,\pmb I_2)\)。于是前者是隐含类的差异的数据;后者没有(或说只有 1 个类),因为它仅仅是普通的高斯分布。通常会使用多元高斯分布或者多元平均分布,更好的空分布选择请参考 Reference。
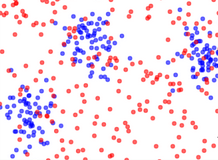
图中蓝色数据为要求的样本的数据,可以观察到大约包含三个类;红色数据为选择的空分布产生的数据,没有明显的类的差异。
为了直观化这一方法的合理性,考虑如果数据中真的有 K 个类的话,那么可以想见:\(W_k\) 将在 \(k\le K\) 时下降较快,而在 \(k>K\) 之后下降较慢。对于我们寻找到的空分布则 \(W_{k,\mathrm{null}}\) 会以一个比较平稳的速率关于 \(k\) 下降。那么可以通过寻找 \(\mathrm{Gap}_N(k)\) 的最大值,即两者之间的差异来实现寻找最合适的 \(k\)。
选择完空分布之后,从该空分布中选择 \(N\) 个数据再进行聚类得到相应的分散度 \(W_{k,\mathrm{null}}\),求其期望则得到 \(\mathbb E_{\mathrm{null}}[\ln W_{k,\mathrm{null}}]\)。但由于这一期望实际上是不可求得的,可以通过几次抽样和一个调整值来近似计算。用蒙特卡罗方法从空分布中获得数据,令 \(B\) 为抽样次数,\(\mathrm{sd}\) 为结果的标准差,那么获得一个误差 \(s_k\),最终结果需要满足
K-均值聚类++算法
这一算法相比标准得的 k-均值聚类可以获得更好的性能
- 在样本中随机选择一个中心点;
- 选择离现有中心点最远的点作为新的中心点,直到获得 k 个中心点;
- 使用标准的 k-均值聚类处理这 k 个中心点。
def k_means_pp(a:np.ndarray, k:int):
"""take an NxD numpy matrix as input"""
n, d = a.shape
clusters = np.empty((k, d))
distances = np.empty((n, ))
clusters[0] = a[np.random.randint(n, size=(1, ))]
for i in range(1, k):
distances = (
(a - clusters[:i].reshape(1, i, d).transpose(1, 0, 2)) ** 2
).sum(axis=-1).min(axis=0)
clusters[i] = a[distances.argmax()]
return k_means(a, k, clusters)
从直观上,这一算法使得每个中心点都被初始化得比较分离。
K-中心点算法
def k_medoids(a:np.ndarray, k:int):
"""take an NxD numpy matrix as input"""
n, d = a.shape
responses = np.random.randint(k, size=(n, ))
while True:
for i in range(k):
chosen = a[responses == i]
distances = np.abs(
chosen.reshape(1, *chosen.shape).transpose(1, 0, 2) - chosen
).sum(axis=(1, 2))
clusters[i] = chosen[np.argmin(distances)]
new_responses = np.abs(
a.reshape(1, *a.shape).transpose(1, 0, 2) - clusters
).sum(axis=-1).argmin(axis=-1)
if (new_responses == responses).all():
return responses, clusters
responses = new_responses
和均值算法的不同在于 for i in range(k) 这一段(更新中心点),主要是中心点的选择方式。
Reference
Finding the K in K-Means Clustering
层级聚类
前述的聚类方法依赖于超参数 \(k\) 和初始化的 \(k\) 个中心点,即使是优化了初始化的++方法也仍然依赖于超参数,这就为算法带来了不稳定性。层级聚类方法中的凝聚聚类就避免了这两个不稳定因素。
凝聚聚类
层级凝聚聚类没有固定的中心点数量 \(k\),而是用数据构自底向上地建出一个树结构。
- 首先将所有数据看作不同的(叶)节点;
- 每次选择两个最近的节点合成为一个新的节点,等同于用两个子节点作为左子树和右子树构建新节点的过程;
- 重复以上过程直到根节点。
算法的关键是看距离 dist 和新的节点 union 是如何计算的。
class Node:
def __init__(self, value, left=None, right=None):
self.value = value
self.left = left
self.right = right
self.count = (left.count + right.count
if left and right else 1)
def __repr__(self):
return f'Node({self.count}): {repr(self.value)}'
__str__ = __repr__
def __eq__(self, other):
return (
self.count == other.count and
(self.value == other.value).all() and
self.left == other.left and
self.right == other.right
)
def agglomerative_clustering(a):
def update(arr, union, p1, p2):
arr[p1] = union
if p2 != (last := arr.shape[0] - 1):
arr[p2] = arr[last]
return arr[:last]
a = a.astype(np.float64)
nodes = np.apply_along_axis(Node, 1, a)
while len(nodes) != 1:
# calculate distances
min_dist = np.inf
for i in reversed(range(1, a.shape[0])):
dist = ((a[i] - a[:i]) ** 2).sum(axis=-1)
min_arg = dist.argmin()
if (d := dist[min_arg]) < min_dist:
min_dist = d
min_pos = min_arg, i
# get nearest two and merge
p1, p2 = pos = list(min_pos)
union_datum = np.average(a[pos],
weights=[n.count for n in nodes[pos]],
axis=0)
union_node = Node(union_datum, nodes[p1], nodes[p2])
a = update(a, union_datum, p1, p2)
nodes = update(nodes, union_node, p1, p2)
return nodes[0]
这里 dist 使用中心点之间的欧氏距离,union 则使用了按中心点所代表的数据量加权取平均。
提取出这两个方法,得到更加普遍的算法
def agglomerative_clustering(a):
def distance(n1, n2):
return ((n1.value - n2.value) ** 2).sum()
def update(nodes, pos):
p1, p2 = pos
nearest_two = nodes[[p1, p2]]
value = np.average([n.value for n in nearest_two],
weights=[n.count for n in nearest_two],
axis=0)
nodes[p1] = Node(value, nearest_two[0], nearest_two[1])
if p2 != (last := nodes.size - 1):
nodes[p2] = nodes[last]
return nodes[:last]
nodes = np.apply_along_axis(Node, 1, a)
while len(nodes) != 1:
min_dist = np.inf
for i in reversed(range(1, nodes.size)):
for j in reversed(range(i)):
dist = distance(nodes[i], nodes[j])
if dist < min_dist:
min_dist = dist
min_pos = j, i
nodes = update(nodes, min_pos)
print(nodes.size)
return nodes[0]
计算距离
使用中心点之间的欧氏距离和中心点所代表的数据量来计算 dist, union 是一种比较直觉但粗糙的方法。
如果每个节点不是加权取平均获得新的中心点,而是将所有子节点的数据进行保存,可以获得其他新的距离计算方法。包括 single_link, complete_linkage, average_linkage, centroid。此时不必保持节点的左右子树了。
class Node:
def __init__(self, value):
self.value = value
def update(nodes, pos):
p1, p2 = pos
nodes[p1].value = np.vstack((
nodes[p1].value,
nodes[p2].value
))
if p2 != (last := nodes.size - 1):
nodes[p2] = nodes[last]
return nodes[:last]
def single_link(n1, n2):
v1, v2 = n1.value, n2.value
v2 = v2.reshape(1, *v2.shape).transpose(1, 0, 2)
dist = np.sqrt(
((v1 - v2) ** 2).sum(axis=-1)
).min()
return dist
def complete_linkage(n1, n2):
v1, v2 = n1.value, n2.value
v2 = v2.reshape(1, *v2.shape).transpose(1, 0, 2)
dist = np.sqrt(
((v1 - v2) ** 2).sum(axis=-1)
).max()
return dist
def average_linkage(n1, n2):
v1, v2 = n1.value, n2.value
n = v1.shape[0] + v2.shape[0]
v2 = v2.reshape(1, *v2.shape).transpose(1, 0, 2)
dist = np.sqrt(
((v1 - v2) ** 2).sum(axis=-1)
).sum() / n
return dist
def centroid(n1, n2):
v1 = np.average(n1.value, axis=0)
v2 = np.average(n2.value, axis=0)
dist = np.sqrt(((v1 - v2) ** 2).sum())
return dist
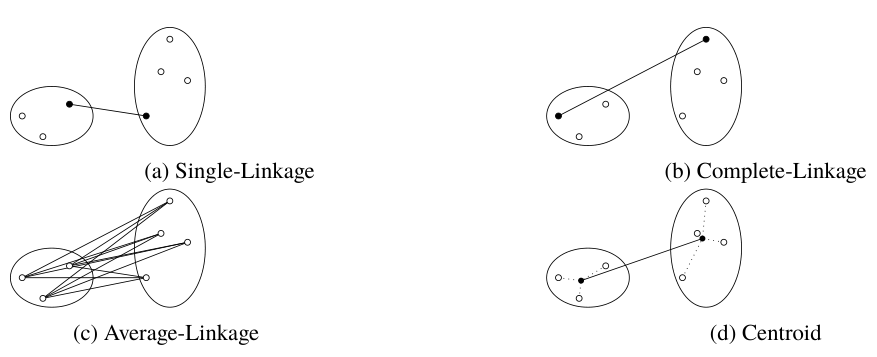
这些方法即使计算距离的方法,又是选择新的中心点的方法,因为节点的更新只是将两个子节点的数据进行结合。其中 single_linkage 选择两个类中最近的两个点,意味着边缘比较接近的两个类更容易融合为新的类;complete_linkage 选择最远的两个点,聚集在一起的类会比较容易融合(欧氏距离下表现为超球体);而其余两个方法都是更加折衷的。
single_linkage 选择边缘的、局部的数据,因此对于一些分布诡吊的数据会更适应。
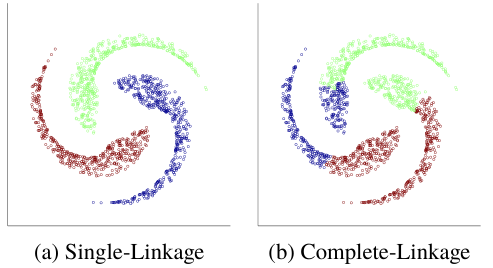
complete_linkage 看重整体的距离,因此对于形状普通的数据更适应,就好像有一个超球体在衡量两个类的聚集程度(欧氏距离下)。
分裂聚类
层次聚类方法中的分裂聚类与凝聚聚类相反,采用的是自顶向下的过程,每层使用一般的平面聚类方法(比如 K-均值聚类),也就是对已经分类的数据再一次分类。因此具有平面聚类方法同样的不稳定性。
def divisive_cluster(a, flat_cluster, k):
def sub_divide(sub_a):
r, c = flat_cluster(sub_a, k)
responses = r.reshape(-1, 1).tolist()
clusters = [[cluster] for cluster in c]
for i in range(k):
choose = r == i
chosen = sub_a[choose]
if chosen.shape[0] not in [0, 1]:
sub_r, sub_c = sub_divide(chosen)
for pos, sub_responses in zip(np.argwhere(choose).ravel(),
sub_r):
responses[pos] += sub_responses
clusters[i].append(sub_c)
return responses, clusters
return sub_divide(a)
数据的分类自然也是(自顶向下)分层的:responses 是每个数据的分类,responses[i][j] 为第 i 个数据的第 j 级分类;clusters 为每个分类的中心点,clusters[k][j] 为第 k 个中心点。获得第 index 个数据的中心点的函数为
def response_clusters(index, responses, clusters):
result = []
*r, last = responses[index]
for i in r:
c, clusters = clusters[i]
result.append(c)
result.append(clusters[last][0])
return result



 浙公网安备 33010602011771号
浙公网安备 33010602011771号