向量分界线

算法分出 \(n\) 个类（\(c_1,c_2,\dots,c_n\)）之后，得到 \(n\) 个向量 \(\pmb w\)，分类方法为 \(c=\underset{c_i\in[c_1,\dots,c_n]}{\arg\max}\pmb w_i^T\pmb x\)。

求 \(\pmb w_1\) 和其他向量 \(\pmb w_2,\dots,\pmb w_n\) 的分界线 \(\pmb s_1\)，满足 \(\pmb w_1^T\pmb s_1=\max_{i\in[2..n]}\pmb w_i^T\pmb s_1\\\)。

• 分界线的存在

  由于对于任何类至少存在一个向量属于这个类，所以必定有属于这个类的分界线

  \[\begin{align*} \text{因为}&\ \forall c_k\in[c_1,\dots,c_n]\exists\pmb x\in\mathbb R^n\left[c_k=\underset{c_i\in[c_1,\dots,c_n]}{\arg\max}\pmb w_k^T\pmb x\right]\\ \text{所以}&\ \forall c_k\in[c_1,\dots,c_n]\exists\pmb s_k\in\mathbb R^n\left[\pmb w_k^T\pmb s_k=\max_{i\in[1..n],i\ne k}\pmb w_i^T\pmb s_k\right]\\ \end{align*} \]

• 分界线的顺序

  将向量写作极坐标形式 \(\left[\langle\rho_1,\theta_1\rangle,\dots,\langle\rho_1,\theta_n\rangle\right]\)，向量 \(\langle\rho_i,\theta_i\rangle,\langle\rho_j,\theta_j\rangle\) 的分界角写作 \(\phi_{ij}\)。

  满足 \(\rho_i\cos(\phi_{ij}-\theta_i)=\rho_j\cos(\phi_{ij}-\theta_j)\)

  \[\begin{align*} \text{假设三个向量满足}&&&\theta_1<\theta_2<\theta_3,\ \left(\theta_1,\theta_2,\theta_3\in[0,\pi)\right)\\ \text{所以}&&&\begin{cases} \rho_1\cos(\phi_{12}-\theta_1)=\rho_2\cos(\phi_{12}-\theta_2)\\ \rho_2\cos(\phi_{23}-\theta_2)=\rho_3\cos(\phi_{23}-\theta_3)\\ \end{cases}\\ &&&\rho_1{\cos(\phi_{12}-\theta_1)\over\cos(\phi_{12}-\theta_2)}=\rho_3{\cos(\phi_{23}-\theta_3)\over\cos(\phi_{23}-\theta_2)}=\rho_2\\ \text{因为至少有一个量属于 2 类, 所以}&&&\exists\phi\left[\rho_2>\rho_1{\cos(\phi-\theta_1)\over\cos(\phi-\theta_2)}\wedge\rho_2>\rho_3{\cos(\phi-\theta_3)\over\cos(\phi-\theta_2)}\right]\\ &&&\exists\phi\left[{\cos(\phi_{12}-\theta_1)\over\cos(\phi_{12}-\theta_2)}>{\cos(\phi-\theta_1)\over\cos(\phi-\theta_2)}\wedge{\cos(\phi_{23}-\theta_3)\over\cos(\phi_{23}-\theta_2)}>{\cos(\phi-\theta_3)\over\cos(\phi-\theta_2)}\right]\\ \text{因为}&&&{\mathrm{d}\over\mathrm{d}\phi}\left[{\cos(\phi-\theta_1)\over\cos(\phi-\theta_2)}\right]={\sin(\theta_1-\theta_2)\over\cos^2(\phi-\theta_2)}<0,{\mathrm{d}\over\mathrm{d}\phi}\left[{\cos(\phi-\theta_3)\over\cos(\phi-\theta_2)}\right]={\sin(\theta_3-\theta_2)\over\cos^2(\phi-\theta_2)}>0\\ \text{所以}&&&\phi_{12}<\phi<\phi_{23}\\ \text{即}&&&\phi_{12}<\phi_{23} \end{align*} \]

  所以分界角的顺序和向量的角度顺序相同。

  对于 \(\theta_1,\theta_2,\theta_3\in[0,2\pi)\) 的情况，只需要调整向量顺序使得 \(\theta_2-\theta_1,\theta_3-\theta_2<\pi\)，结论依旧成立。

  从直观上理解，如果分界线不按顺序，会使得 \(\pmb w_2^T\pmb x<\max(\pmb w_1^T\pmb x,\pmb w_3^T\pmb x)\) 恒成立，使任何向量都不属于 2 类。

  如图（左侧按顺序，右侧不按顺序）

  

• 接近的类有接近的分界角

  

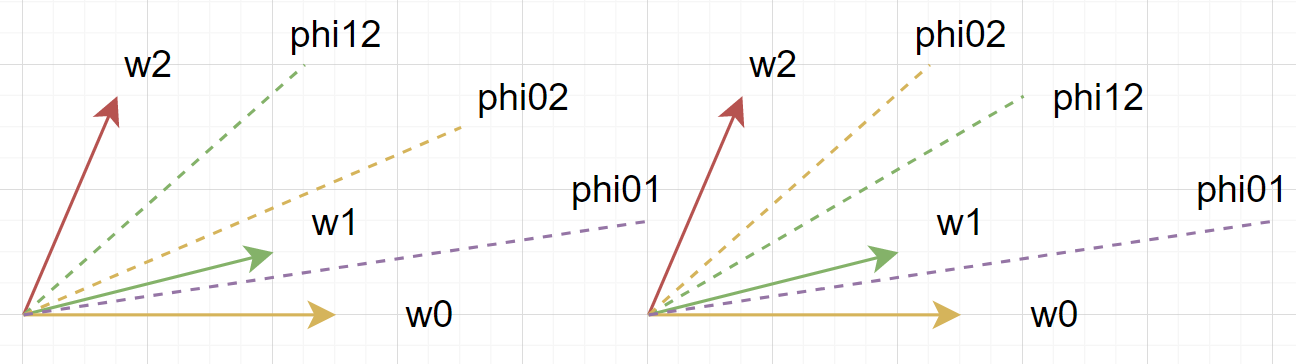
  左侧为满足题意的情况，右侧为不满足题意的情况。

  仍然考虑三个向量，由上一条已知 \(\phi_{01}<\phi_{12}\)，证明 \(\phi_{02}<\phi_{12}\)

  实际上证明方法和上一证明相同，但需要多次使用 \({\mathrm{d}\over\mathrm{d}\phi}\left[{\cos(\phi-\theta_1)\over\cos(\phi-\theta_2)}\right]\) 的结果，在下面的每一步中都要使用这个导数。

  使用反证法，令 \(\phi_{02}\ge\phi_{12}\)

  \[\begin{align*} \phi_{02}\ge\phi_{12}&\implies\begin{cases} \rho_0\cos(\phi_{02}-\theta_0)=\rho_2\cos(\phi_{02}-\theta_2)\\ \rho_1\cos(\phi_{12}-\theta_0)=\rho_2\cos(\phi_{12}-\theta_2)\\ \end{cases}\\ &\implies\forall\phi\in[\phi_{12},\phi_{02}][\rho_0\cos(\phi-\theta_0)\ge\rho_2\cos(\phi-\theta_2)\ge\rho_1\cos(\phi-\theta_1)]且等号不能同时取得\\ &\implies\forall\phi\in[\phi_{12},\phi_{02}][\rho_0\cos(\phi-\theta_0)>\rho_1\cos(\phi-\theta_1)]\\ &\overset{\phi_{01}<\phi_{12}\le\phi_{02}}{\implies}\forall\phi\in(\phi_{01},\phi_{02}][\rho_0\cos(\phi-\theta_0)>\rho_1\cos(\phi-\theta_1)],\text{ 与分界角 $\phi_{01}$ 的分界效果冲突}\\ \end{align*} \]

  这个证明的关键在 \(\rho_0\cos(\phi-\theta_0)\ge\rho_2\cos(\phi-\theta_2)\ge\rho_1\cos(\phi-\theta_1)\)，表明 \(\pmb w_0\) 先于 \(\pmb w_1\) 随着角度的减小获得了更大的值。

由上述三个引理，求 \(\pmb w_k^T\pmb s_k=\max_{i\in[1..n],i\ne k}\pmb w_i^T\pmb s_k\\\)，只需要求 \(\pmb w_k^T\pmb s_{k.left}=\pmb w_{k-1}^T\pmb s_{k.left}\\\) 和 \(\pmb w_k^T\pmb s_{k.right}=\pmb w_{k+1}^T\pmb s_{k.right}\\\)，其中 \(\pmb w_i\) 按角度顺序排列好。