基本公式
\[\begin{align*}
F(x)&=P\lbrace X\le x\rbrace=\frac1{1+e^{(\mu-x)/\gamma}}\\
f(x)&=F^\prime(x)={e^{(\mu-x)/\gamma}\over\gamma(1+e^{(\mu-x/\gamma)})^2}
\end{align*}
\]
\(F(x)\) 关于 \((\mu,\frac12)\) 对称。
二项逻辑回归(binomial logistic regression model)
\[\begin{align*}
P(Y\mid \pmb X;\pmb w)=
{\exp({\pmb w}^T\pmb x)\over1+\exp({\pmb w}^T\pmb x)}={1\over1+\exp(-{\pmb w}^T\pmb x)}
\end{align*}
\]
对数几率(log odds)函数 \(logit(p)=\ln\left({p\over1-p}\right)\)\(,\)\(logit[P(Y\mid \pmb X;\pmb w)]={\pmb w}^T\pmb x\)
预设
- 用于二分类问题,\(Y\in\lbrace0,1\rbrace\sim Bernoulli(p),P(y\mid p)=p^y(1-p)^{1-y}\),令 \(p={1\over1+\exp(-{\pmb w}^T\pmb x)}\) 则得到二项逻辑回归;
- 所有样本 \(P(Y=y_i\mid \pmb x=\pmb x_i)\) 独立;
极大化对数似然函数
因为假设 \(y\) 服从伯努利分布,选择似然函数
\[\begin{align*}
\mathcal L(\pmb Y\mid\pmb X;\pmb w)&=\prod_{y_i\in\pmb Y,y_i=1}P(y_i=1\mid\pmb x_i,\pmb w)\cdot\prod_{y_i\in\pmb Y,y_i=0}P(y_i=0\mid\pmb x_i,\pmb w)\\
&\xlongequal{P(y_i=1\mid\pmb x_i,\pmb w)\leftarrow p_i,\ P(y_i=0\mid\pmb x_i,\pmb w)\leftarrow 1-p_i}\\
&=\prod_{y_i\in\pmb Y,y_i=1}p_i\cdot\prod_{y_i\in\pmb Y,y_i=0}(1-p_i)\\
&=\prod_{y_i\in\pmb Y}p_i^{y_i}\cdot(1-p_i)^{1-y_i}
\end{align*}
\]
其中 \(\pmb X\) 为选择的样本;\(\pmb Y\) 为选择的样本的标签,在这里表示所有样本都被计算。\(y_i\in Y,y_i=1\) 表示选择所有标签为 \(1\) 的样本 \(\pmb x_i\),反之亦然。\(p_i\) 为 sigmoid 函数 \(\frac1{1+\exp(-\pmb w^T\pmb x_i)}\)。
取对数再取平均获得对数似然函数 \(\ln\mathcal L(\pmb Y\mid\pmb X;\pmb w)=\frac1N\sum_{i\in[1..N]}y_i\ln p_i+(1-y_i)\ln (1-p_i)\)
\[\begin{align*}
\nabla_{\pmb w}\ln\mathcal L&=\frac1N\sum_{i\in[1..N]}\pmb x_i(y_i-p_i)\\
p_i&=\frac1{1+\exp(-\pmb w^T\pmb x_i)}
\end{align*}
\]
概率和似然(Probability vs Likelihood)
假设有一个概率分布函数 \(P(X;\theta)\)。
梯度下降法
为了最大化似然函数
\(\pmb w^{t+1}\leftarrow\pmb w^t+\eta\nabla_{\pmb w}\ln\mathcal L(\pmb Y\mid\pmb X;\pmb w^{(t)})\),其中 \(\eta>0\) 为超参数学习率(learning rate),\(\pmb X,\pmb Y\) 为选择的样本和对应的标签。
牛顿法
用 \(\mathcal L(\pmb w)\) 表示 \(\mathcal L(\pmb Y\mid\pmb X;\pmb w)\),\(\mathcal{\pmb H}_{\pmb w_0}\) 表示 \(\mathcal L(\pmb w)\) 在 \(\pmb w_0\) 的 Hessian 矩阵。
\[\begin{align*}
\mathcal L(\pmb w)&\approx\mathcal L(\pmb w_0)+\nabla^T_{\pmb w}[\mathcal L(\pmb w_0)]\cdot(\pmb w-\pmb w_0)+\frac12(\pmb w-\pmb w_0)^T{\mathcal{\pmb H}_{\pmb w_0}}(\pmb w-\pmb w_0)\\
\nabla_{\pmb w}\mathcal L(\pmb w)&\approx\nabla_{\pmb w}\mathcal L(\pmb w_0)+\mathcal{\pmb H}_{\pmb w_0}(\pmb w-\pmb w_0)\\
\end{align*}
\]
令 \(\nabla_{\pmb w}\mathcal L(\pmb w^{(t+1)})=0,\pmb w_0\leftarrow \pmb w^{(t)}\)。
\[\begin{align*}
\nabla_{\pmb w}\mathcal L(\pmb w^{(t)})+\mathcal{\pmb H}_{\pmb w^{(t)}}(\pmb w^{(t+1)}-\pmb w^{(t)})&=0\\
\pmb w^{(t+1)}&=\pmb w^{(t)}-\mathcal{\pmb H}_{\pmb w^{(t)}}^{-1}\cdot\nabla_{\pmb w}\mathcal L(\pmb w^{(t)})
\end{align*}
\]
得到迭代公式 \(\pmb w^{(t+1)}\leftarrow\pmb w^{(t)}-\mathcal{\pmb H}_{\pmb w^{(t)}}^{-1}\cdot\nabla_{\pmb w}\mathcal L(\pmb w^{(t)})\)。
事实上,\(\mathcal L\) 可以改为任意损失函数,则得到任意损失函数的牛顿法。
样本的线性可分性和超平面不收敛的情况
证明:当样本线性可分时,超平面不收敛。
证明方法一:
如果存在超平面 \(\pmb w^T\pmb x=0\),使得所有样本都被正确分类,那么令超平面与一个系数 \(c\) 相乘不改变此超平面 \(c\pmb w^T\pmb x=0\)。
\[\begin{align*}
p_i&=\frac1{1+\exp(-c\pmb w^T\pmb x)}\\
\ln\mathcal L&=\sum_iy_i\ln p_i+(1-y_i)\ln(1-p_i)\\
\frac\partial{\partial c}\ln\mathcal L&=\sum_iy_i(\pmb w^T\pmb x)-{\pmb w^T\pmb x\over1+\exp(-c\pmb w^T\pmb x)}\\
&=\sum_i(y_i-\frac1{1+\exp(-c\pmb w^T\pmb x)})\pmb w^T\pmb x\\
&=\sum_i(y_i-p_i)\pmb w^T\pmb x
\end{align*}
\]
由于所有样本都被正确分类,所以 \(y_i=1\implies\pmb w^T\pmb x>0,y_i=0\implies\pmb w^T\pmb x<0\)
所以 \(\frac\partial{\partial c}\ln\mathcal L>0\),则增加 \(c\) 恒提高似然函数,取最大似然函数则 \(c\to\infty\)。将 \(c\pmb w^T\) 看作 \(\pmb w^T\),则 \(\pmb w^T\to\infty\pmb w^T\)。
证明方法二:
\[\begin{align*}
&y_i=1\iff\pmb w^T\pmb x_i>0\iff p_i>\frac12\\
&y_i=0\iff\pmb w^T\pmb x_i<0\iff p_i<\frac12\\
\implies&\pmb w^T\pmb x_i(p_i-y_i)<0\\
\implies&\pmb w-\eta\pmb x_i(p_i-y_i)\text{ 在超平面与 $\pmb w$ 同侧延伸}
\end{align*}
\]
且以上 \(\vert p_i-y_i\vert>\frac12\),\(\pmb x\) 作为样本长度固定,所以不收敛
改善方法
添加 \(L^2\) 范数改善
\[\begin{align*}
\ln\mathcal L-\frac\lambda2\vert\vert\pmb w\vert\vert^2_2&=\sum_iy_i\ln p_i+(1-y_i)\ln(1-p_i)-\frac\lambda2\pmb w^T\pmb w\\
\nabla_{\pmb w}\left[\ln\mathcal L-\frac\lambda2\pmb w^T\pmb w\right]&=\sum_i\pmb x_i(y_i-p_i)-\lambda\pmb w\\
\pmb w^{(t+1)}&\leftarrow\pmb w^{(t)}+\frac\eta N(\nabla_{\pmb w}\left[\ln\mathcal L-\frac\lambda2\pmb w^T\pmb w\right])\\
&=\left(1-{\eta\lambda\over N}\right)\pmb w^{(t)}+\frac\eta N\left[\sum_i\pmb x_i(y_i-p_i)\right]
\end{align*}
\]
当 \(\pmb w\) 过大时,\(\frac\eta N\left[\sum_i\pmb x_i(y_i-p_i)\right]\) 带来的增益小于 \({\eta\lambda\over N}\pmb w^{(t)}\) 带来的损失。
添加标签平滑(label smoothing)改善,\(y_i\in\lbrace0,1\rbrace\) 改为 \(y_i\in\lbrace\sigma,1-\sigma\rbrace,\sigma\in(0,1/2)\ 接近\ 0\)。
\[\begin{align*}
y_i&\in\lbrace\sigma,1-\sigma\rbrace\\
p_i&=\frac1{1+\exp(-\pmb w^T\pmb x)}\\
\pmb w^{(t+1)}&\leftarrow\pmb w^{(t)}-\eta\pmb x_i(p_i-y_i)
\end{align*}
\]
当 \(\pmb w\) 过大时,\(y_i=\sigma\implies\pmb w^T\pmb x\ll0\implies p_i\to0\implies\pmb w^{(t)},\eta\pmb x_i(p_i-y_i)\text{ 在超平面同侧}\),\(y_i=1-\sigma\) 时也成立。
推广到多项逻辑回归
- one-vs-rest
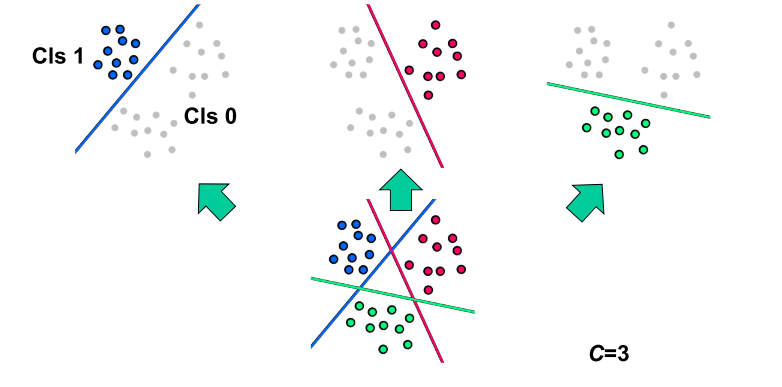
- one-vs-one
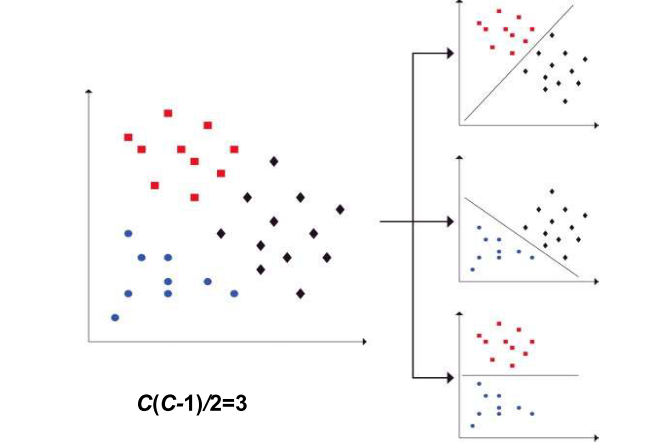
总之,对上述每个分类进行学习,可以获得 \(K=\begin{cases}C&\text{one-vs-rest}\\\binom C2&\text{one-vs-one}\end{cases}\) 个 \(\pmb w\),这些 \(\pmb w\) 一起可以获得 \(K\) 个二项逻辑回归,选择其中最大的一个类即可,\(\hat y=\underset{c\in\lbrace1,\dots,C\rbrace}{\arg\max}P(Y=c\mid\pmb x)\)。
sigmoid function
为了将在数轴上任意的 \(z\) 映射到 \((0,1)\) 上,从直觉上构造函数
\[\begin{align*}
\begin{array}{rcl}
-\infty<&z&<\infty\\
0<&\exp(z)&<\infty\\
1<&1+\exp(z)&<\infty\\
1>&\frac1{1+\exp(z)}&>0\\
0<&\frac1{1+\exp(-z)}&<1\\
\end{array}
\end{align*}
\]
因此选择函数 \(S(z)=\frac1{1+\exp(-z)}\) 。之后发现这个函数的导数不错,\(S^\prime(z)=S(z)[1-S(z)]\),在 0 附近较大,而在其他情况较小。
使用标签 \(y\in\lbrace-1,1\rbrace\)
\[\begin{align*}
\tanh(z)&={e^z-e^{-z}\over e^z+e^{-z}}=2Sigmoid(2z)-1\\
\tanh^\prime(z)&=1-\tanh^2(z)
\end{align*}
\]
依旧构造似然函数
\[\begin{align*}
p_i&=\tanh(\pmb w^T\pmb x)\\[0.3cm]
\mathcal L(\pmb Y\mid\pmb X;\pmb w)&=\prod_{y_i\in\pmb Y,y_i=1}P(y_i=1\mid\pmb x_i,\pmb w)\cdot\prod_{y_i\in\pmb Y,y_i=-1}P(y_i=0\mid\pmb x_i,\pmb w)\\
&\xlongequal{P(y_i=1\mid\pmb x_i,\pmb w)\leftarrow{(1+p_i)/2},\ P(y_i=-1\mid\pmb x_i,\pmb w)\leftarrow(1-p_i)/2}\\
&=\prod_{y_i\in\pmb Y,y_i=1}\frac{1+p_i}2\cdot\prod_{y_i\in\pmb Y,y_i=-1}\frac{1-p_i}2\\
&=\prod_{y_i\in\pmb Y}\left(\frac{1+p_i}2\right)^{(y_i+1)/2}\cdot\left(\frac{1-p_i}2\right)^{(1-y_i)/2}\\
\frac1N\ln\mathcal L(\pmb Y\mid\pmb X;\pmb w)&=\frac1{2N}\sum_{i=[1..N]}(y_i+1)\ln\left(\frac{1+p_i}2\right)+(1-y_i)\ln\left(\frac{1-p_i}2\right)\\
\nabla_{\pmb w}\frac1N\ln\mathcal L(\pmb Y\mid\pmb X;\pmb w)&=\frac1N\sum_{i=[1..N]}\pmb x_i\left(y_i-p_i\right)\\
\end{align*}
\]
出于计算方便
\(S^\prime(z)=S(z)[1-S(z)]\) 所以选择 \(p_i,(1-p_i)\)
\(\tanh^\prime(z)=[1+\tanh(z)][1-\tanh(z)]\),所以选择 \((1+p_i)/2,(1-p_i)/2\)
事实上 \((1+p_i)/2=Sigmoid(2\pmb w^T\pmb x_i),(1-p_i)/2=1-Sigmoid(2\pmb w^T\pmb x_i)\),相当于 \(y_i\to(y_i+1)/2,p_i\to(p_i+1)/2,\pmb x_i\to2\pmb x_i\) 所以得出相同的结果。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号