园龄：粉丝：关注：

2022-10-27 11:48阅读: 60评论: 0推荐: 0

类型系统与程序语言——无类型系统

无类型系统

无类型系统

本节为其他章节作引。

无类型算数表达式

一门语言需要语法、语义、语用来构成。现在以无类型算数表达式这个非常简单的语言开始探讨，我们将明确它的语法和语义来充分了解这门语言。

语法

无类型算数表达式语言的语法中只包含 $t r u e, f a l s e, 0, succ, pred, iszero$ 和条件表达式，通过堆砌这些语法就完成了这门语言的“代码”。

我们将这门语言中的成分称为 term，一个语言的所有内容就是所有 term 的集合，在这门语言中 term 的集合是具有如下性质的最小的 $T$ ，如下：

\begin{aligned} {t r u e, f a l s e, 0} & \subseteq T, \\ if t_{1} \in T, then {succ t_{1}, pred t_{1}, iszero t_{1}} & \subseteq T, \\ if t_{1}, t_{2}, t_{3} \in T, then i f t_{1} t h e n t_{2} e l s e t_{3} & \subseteq T . \end{aligned}

或者使用推理规则定义如下：

\begin{array}{r} {t r u e, f a l s e, 0} \subseteq T \\ t_{1} \in T \\ {succ t_{1}, pred t_{1}, iszero t_{1}} \subseteq T \\ t_{1}, t_{2}, t_{3} \in T \\ if t_{1} then t_{2} else t_{3} \in T \end{array}

也可以使用集合的方法定义，先定义集合 $S_{i}$ 和 $S$

\begin{aligned} S_{0} & = \emptyset, \\ S_{i + 1} & = {t r u e, f a l s e, 0} \\ \cup {succ t_{1}, pred t_{1}, iszero t_{1} : t_{1} \in S_{i}} \\ \cup {if t_{1} then t_{2} else t_{3} : t_{1}, t_{2}, t_{3} \in S_{i}}, \\ S & = ⋃_{i} S_{i} . \end{aligned}

再证明： $T = S$

熟悉命题逻辑的应该能看出这类似于对全体合式公式的集合的自底向上的定义，只需证明 $S$ 符合 $T$ 的定义，且为最小即可。

先证明前者：

\begin{aligned} S_{1} & = {t r u e, f a l s e, 0} \subseteq S, \\ \forall t_{1} \in S, \exists S_{i} (t_{1} \in S_{i}) & ⟹ \forall t_{1} \in S (succ t_{1} \in S_{i + 1}) \\ ⟹ \forall t_{1} \in S (succ t_{1} \in S), \\ so as & pred t_{1}, iszero t_{1}, if t_{1} then t_{2} else t_{3} . \end{aligned}

接下来使用归纳法证明最小，先定义 $S^{'}$ 为任意满足 $T$ 的集合，只需证明 $S_{i} \subseteq S^{'}$ ：

\begin{array}{r} \forall j < i (S_{j} \subseteq S) ⟹ {\begin{cases} S_{i} & = S_{0} = \emptyset \subseteq S & i = 0, \\ S_{i} & = S_{max j + 1} & i \neq 0 \\ = {t r u e, f a l s e, 0} \\ \cup {succ t_{1}, pred t_{1}, iszero t_{1} : t_{1} \in S_{max j}} \\ \cup {i f t_{1} t h e n t_{2} e l s e t_{3} : t_{1}, t_{2}, t_{3} \in S_{max j}} \\ \subseteq S^{'} \end{cases} \end{array}

$S = ⋃_{i} S_{i}$ ，则 $S \subseteq S^{'}$ ，由于 $S^{'}$ 为任意大小的满足 $T$ 的集合，故 $S$ 为最小的满足 $T$ 的集合。

其他定义

\begin{array}{ll} C o n s t s (t r u e) & = {t r u e} \\ C o n s t s (f a l s e) & = {f a l s e} \\ C o n s t s (0) & = {0} \\ C o n s t s (succ t_{1}) & = C o n s t s (t_{1}) \\ C o n s t s (pred t_{1}) & = C o n s t s (t_{1}) \\ C o n s t s (iszero t_{1}) & = C o n s t s (t_{1}) \\ C o n s t s (if t_{1} then t_{2} else t_{3}) & = C o n s t s (t_{1}) \cup C o n s t s (t_{1}) \cup C o n s t s (t_{1}) \end{array}

\begin{array}{ll} s i z e (t r u e) & = 1 \\ s i z e (f a l s e) & = 1 \\ s i z e (0) & = 1 \\ s i z e (succ t_{1}) & = s i z e (t_{1}) + 1 \\ s i z e (pred t_{1}) & = s i z e (t_{1}) + 1 \\ s i z e (iszero t_{1}) & = s i z e (t_{1}) + 1 \\ s i z e (if t_{1} then t_{2} else t_{3}) & = s i z e (t_{1}) + s i z e (t_{2}) + s i z e (t_{3}) + 1 \end{array}

\begin{array}{ll} d e p t h (t r u e) & = 1 \\ d e p t h (f a l s e) & = 1 \\ d e p t h (0) & = 1 \\ d e p t h (succ t_{1}) & = d e p t h (t_{1}) + 1 \\ d e p t h (pred t_{1}) & = d e p t h (t_{1}) + 1 \\ d e p t h (iszero t_{1}) & = d e p t h (t_{1}) + 1 \\ d e p t h (if t_{1} then t_{2} else t_{3}) & = max (d e p t h (t_{1}) + d e p t h (t_{2}) + d e p t h (t_{3})) + 1 \end{array}

由于 $T$ 的归纳定义方法，term 的多种性质可以使用归纳法（以及分类讨论）证明。

比如，证明 $if t \to t^{'} and t \to t^{″}, then t^{'} = t^{″}$ ：

\begin{aligned} t^{'} & = {\begin{cases} t_{2} & t = if t r u e then t_{2} else t_{3} \\ t_{3} & t = if f a l s e then t_{2} else t_{3} \\ if t_{1}^{'} then t_{2} else t_{3} & t = if t_{1} then t_{2} else t_{3} \end{cases} \\ t^{″} & = {\begin{cases} t_{2} & t = if t r u e then t_{2} else t_{3} \\ t_{3} & t = if f a l s e then t_{2} else t_{3} \\ if t_{1}^{″} then t_{2} else t_{3} & t = if t_{1} then t_{2} else t_{3} \end{cases} \end{aligned}

虽然 $t$ 有三种形式，但显然只有第三种情况有区别，如果 $t_{1}^{'} = t_{1}^{″}$ ，则 $t^{'} = t^{″}$ ，这里就需要归纳论证了。

语义

语义是 terms 如何求值（evaluate）的定义，定义语义有三个基本途径：

操作语义（Operational Semantics）

通过定义 terms 如何工作的一系列操作的语义。比如最常见的替换操作和单步求值操作，这两个操作实际上是对 term 的简化。实际上还有可能有更多操作语义。

其实就是程序的执行流程。
指称语义（Denotational Semantics）

将一些 term 与数学实体关联起来的语义，可以明确程序行为。
公理语义（Axiomatic Semantics）

在一套逻辑系统下，研究某种特定的性质是否成立的语义。

求值

Boolean

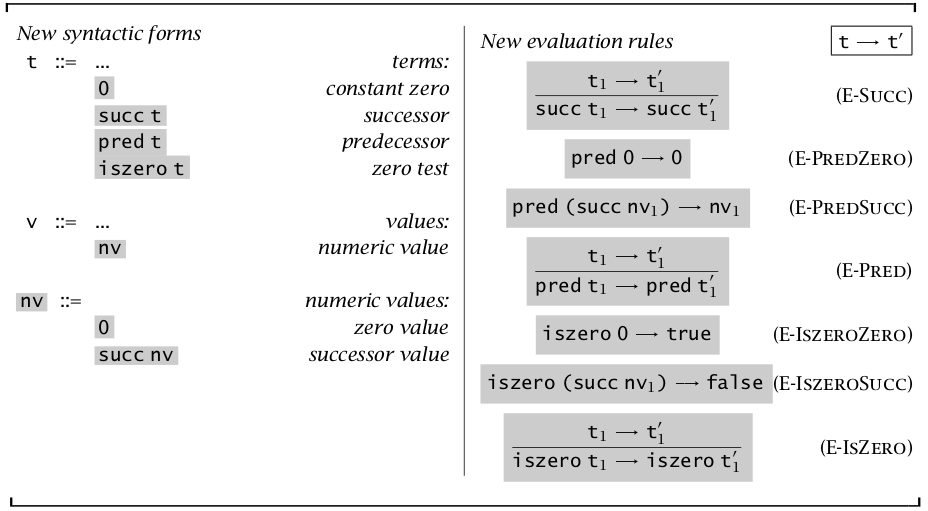
Arithmetic Expressions

图片显示了无类型表达式中的两种成分：Boolean 和自然数的运算。左侧为语法，展示了语言的所有成员，包括 term 和 value，term 和 value 的区别就是 value 是不可再求值的，term 包含 value；右侧为语义，其实也就是一系列推演规则，展示如何在各种前提（或无需前提）下做到 $t \to t^{'}$ ，“ $\to$ ” 是一个非常关键的算符，称为“单步求值”，将 term 逐步计算为 value。

比如下面的运算就将复杂的 term 多步求值为了一个 value —— false。

\begin{aligned} if false then true else (if false then false else false) \\ if false then false else false \\ false \end{aligned}

同时定理【单步求值的确定性】： $if t \to t^{'} and t \to t^{″}, then t^{'} = t^{″}$ 指出，单步求值规则之间不可能冲突，一个 term 在某一时刻要么只适用一条规则，要么不适用任何规则。

由于可能出现如 $succ f a l s e$ 这样不适用任何规则且不是 value 的存在，这种情况称为 stuck，这是一种在语法层面允许出现的运行时错误。

无类型 Lambda 表达式

Lambda 演算是一种形式化系统，在该系统中所有计算都被归约为函数的定义（definition）和应用（application）上的各种操作。如果说无类型算数表达式是过程式语言，那么无类型 Lambda 表达式就是函数式语言了。

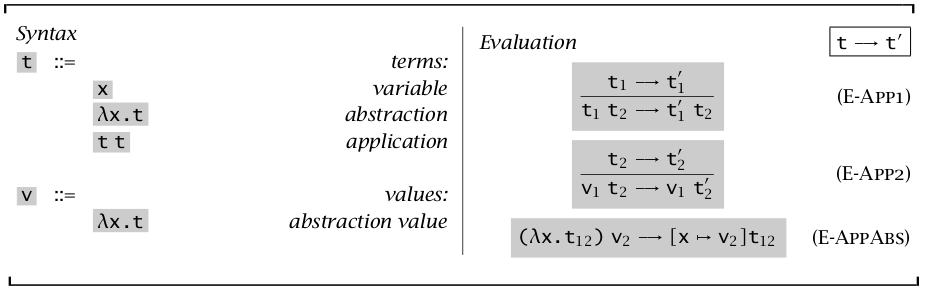
Untyped Lambda-Calculus

语法

\begin{aligned} t ::= & t e r m s : \\ x & v a r i a b l e \\ λ x . t & a b s t r a c t i o n \\ t t & a p p l i c a t i o n \end{aligned}

上述语法表示，该语言中的最小组成单元 term 包括三种类型，左边为这三种类型的形式，右边为这三种形式的名称。

采用集合的定义为， $T$ 为 term 的集合， $V$ 为变量的集合

\begin{array}{l} x \in T for every x \in V \\ if t_{1} \in T and x \in V, then λ x . t_{1} \in T \\ if t_{1} \in T and t_{2} \in T, then t_{1} t_{2} \in T \end{array}

Lambda 演算的作用域和操作语义

Lambda 演算中最重要的就是关于函数的描述，即 $λ x . t$ 或更多参数的函数 $λ x . λ y . t$ 。

用 Python 语言做类比可以理解为 lambda x: t 和 lambda x, y: t，在函数中， $.$ 表示参数定义的结束， $λ$ 代表函数定义的开始， $t$ 可以是任意一个 term。

像很多语言一样，这个演算中的函数也有变量的作用域，依作用于不同分为约束变量和自由变量，比如 $(λ x . x) x$ 中括号中的 $x$ 和括号外 $x$ 是不同的变量。

自由变量的集合也可以被定义为：

\begin{array}{ll} F V (x) & = {x} \\ F V (λ x . t_{1}) & = F V (t_{1}) ∖ {x} \\ F V (t_{1} t_{2}) & = F V (t_{1}) \cup F V (t_{2}) \end{array}

对函数的应用只是简单地将函数体中的 term 中的参数进行替换，表示为 $(λ x . t_{1}) t_{2} \to [x \mapsto t_{2}] t_{1}$ ，比如

\begin{aligned} (λ x . x) y & \to [x \mapsto y] (x) \to y \\ (λ x . λ y . x y) z & \to [x \mapsto z] (λ y . x y) \to λ y . z y \end{aligned}

更严谨的定义为

\begin{array}{llll} [x \mapsto s] x & = & s \\ [x \mapsto s] y & = & y & if y \neq x \\ [x \mapsto s] λ y . t_{1} & = & λ y . [x \mapsto s] t_{1} & if y \neq x and y \notin F V (s) \\ [x \mapsto s] (t_{1} t_{2}) & = & [x \mapsto s] t_{1} [x \mapsto s] t_{2} \end{array}

Lambda 演算编程

布尔运算

可以使用 Lambda 表达式作一些有趣的编程，首先我们定义编程中最基础的一种运算——boolean。

由于在 Lambda 演算中，一切皆函数，所以 $t r u e, f a l s e$ 也是一种函数，其定义为

\begin{aligned} true & = λ t . λ f . t \\ false & = λ t . λ f . f \end{aligned}

可以看到，这一运算仅仅是选择两个参数中的一个，这一行为本身没有什么用处，需要与其配套的布尔运算

\begin{aligned} not & = λ a . a false true \\ and & = λ b . λ c . b c false \\ or & = λ b . λ c . b true c \end{aligned}

尝试将 $a, b, c$ 用 $true, false$ 替换可以得到对应的结果。

序偶

Lambda 演算不仅可以定义运算，还可以定义结构，下面介绍一种最基础的数据结构——序偶。

\begin{aligned} pair & = λ f . λ s . λ b . b f s \\ first & = λ p . p true \\ second & = λ p . p false \end{aligned}

\begin{aligned} first (pair v w) \\ = & first ((λ f . λ s . λ b . b f s) v w) \\ \to & first (λ b . b v w) \\ = & (λ p . p true) (λ b . b v w) \\ \to & (λ b . b v w) true \\ \to & true v w \\ \to & v \end{aligned}

虽然序偶这一结构非常简单，但是实际上可以用不断的序偶来定义元组和数组。一个例子就是 C++ 中的元组就是由序偶的模版组合成的。

自然数

由皮亚诺公里，将数定义为对某函数的重复后继运算，可以得到自然数的 Lambda 演算

\begin{aligned} 0 & = λ f . λ x . x \\ 1 & = λ f . λ x . f x \\ 2 & = λ f . λ x . f (f x) \\ 3 & = λ f . λ x . f (f (f x)) \\ ⋮ \\ n & = λ f . λ x . f^{\circ n} x \end{aligned}

现在有了数，还需要定义数之间的运算，依次定义后继，加法，乘法，前驱，减法

\begin{aligned} succ & = λ n . λ f . λ x . f (n f x) \\ + & = λ m . λ n . λ f . λ x . m succ n \\ = λ m . λ n . λ f . λ x . m f (n f x) \\ \times & = λ m . λ n . m (+ n) 0 \end{aligned}

不要忘记数就是对某个函数的重复应用，所以后继是某个函数再一次应用，加法是后继的重复应用，乘法是加法的重复应用。

接下来定义前驱，这一操作需要用到序偶，先将其思想用 Python 表示为

 def pred(n: int) -> int:
    pair = (0, 0)
    for _ in range(n):
        pair = (pair[1], pair[1] + 1)
    return pair[0]

\begin{aligned} initialize & = pair 0 0 \\ increase & = λ p . pair (second p) (+ 1 (second p)) \\ pred & = λ m . first (m increase initialize) \\ - & = λ m . λ n . n pred m \end{aligned}

除法在这里就不列出具体实现了，只列出其思想：也需要一个序偶，一个数记录减法次数，另一个数记录被减数，多次减法后取减法次数即可。

\begin{aligned} iszero & = λ n . n (λ_. false) true \\ equal & = λ m . λ n . and (iszero (- m n)) (iszero (- n m)) \end{aligned}

拓展

递归

若一个函数具有如下形式，其中 $a, b, c, d$ 为任意函数， $p$ 为谓词

f (x) = {\begin{cases} a (x) & if p (x) \\ b (f (c (x))) + d (x) & else \end{cases}

其 Lambda 演算形式为

\begin{aligned} f i x & = λ f . (λ x . f (λ y . x x y)) (λ x . f (λ y . x x y)) \\ f - h e l p e r & = λ f . λ x . (p x) (a x) (+ (b (f (c x))) (d x)) \\ f & = f i x f - h e l p e r \end{aligned}

$f i x, f - h e l p e r$ 都接受一个函数作为参数， $f - h e l p e r$ 其实就是 $f$ 的函数行为，而 $f i x f - h e l p e r$ 为 $f$ 的展开形式。

\begin{aligned} let f_{h} = & f - h e l p e r \\ f_{f} = & (p x) (a x) (+ (b (f (c x))) (d x)) \\ r e c = & λ x . f_{h} (λ y . x x y) \\ then f = & f i x f_{h} \\ = & r e c r e c \\ = & f_{h} (λ y . r e c r e c y) \\ = & (λ f . λ x . f_{f}) (λ y . r e c r e c y) \\ \to & λ x . [f \mapsto (λ y . r e c r e c y)] f_{f} \\ = & λ x . [f \mapsto (λ y . f y)] f_{f} \end{aligned}

要注意 $[]$ 内的两个 $f$ 含义不同，左边的为 $f_{f}$ 中的 $f$ ，右边的为我们要求的递归函数 $f$ 。

最后的结果表明： $f_{f}$ 内的 $f$ 是对 $(λ y . f y)$ 的再一次应用，其中的 $y$ 其实在 $f_{f}$ 中会被 $c (x)$ 替换。由于 $λ y . f y \leftrightarrow λ y . r e c r e c y$ ，所以在 $f$ 的展开中并没有再次出现 $f$ ，这只是计算上的等价替换，并不是在函数体中再次调用了 $f$ 。

链表

一个链表 $[x, y, z]$ 是形如 $λ c . λ n . c x (c y (c z n))$ 的函数，在其他语言被称为 $r e d u c e$ 。

链表相关运算

\begin{aligned} nil & = λ c . λ n . n \\ cons & = λ h . λ t . λ c . λ n . c h (t c n) \\ isnil & = λ t . t (λ_. λ_. false) true \\ head & = λ t . t true 0 \\ initialize & = pair nil nil \\ increase & = λ x . λ p . pair (second p) (cons x (second p)) \\ tail & = λ t . first (t increase initialize) \end{aligned}

上一篇类型系统与程序语言——简单类型

下一篇Linux Shell 函数

本文作者：violeshnv

本文链接：https://www.cnblogs.com/violeshnv/p/16831709.html

posted @ 2022-10-27 11:48 Violeshnv 阅读(60) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

violeshnv

类型系统与程序语言——无类型系统

无类型系统

无类型算数表达式

语法

语义

求值

无类型 Lambda 表达式

语法

Lambda 演算的作用域和操作语义

Lambda 演算编程

布尔运算

序偶

自然数

拓展

递归

链表

最新随笔

我的标签

合集

随笔分类

随笔档案

	def pred(n: int) -> int:
	pair = (0, 0)
	for _ in range(n):
	pair = (pair[1], pair[1] + 1)
	return pair[0]