带修正因子的Mamdani型模糊算法配合人工势场的机器人路径规划
一、绪论
人工势场算法一种比较常用的机器人路径规划、避障算法,但是普通的人工势场算法容易出现局最优解的问题,本文依托这一问题采用Mamdani型的模糊算法对传统的人工势场算法进行校正,在解决传统人工势场算法中的局部最优解的前题下,优化传统人工势场算法的最优路径。
二、传统人工势场算法
传统人工势场算法通俗的说就是,将目标点人为设置一个引力场,将路径上的所有障碍物人为的设置一个斥力场。根据引力和斥力的合力的作用规避障碍,达到目标点。图解见图(1)。
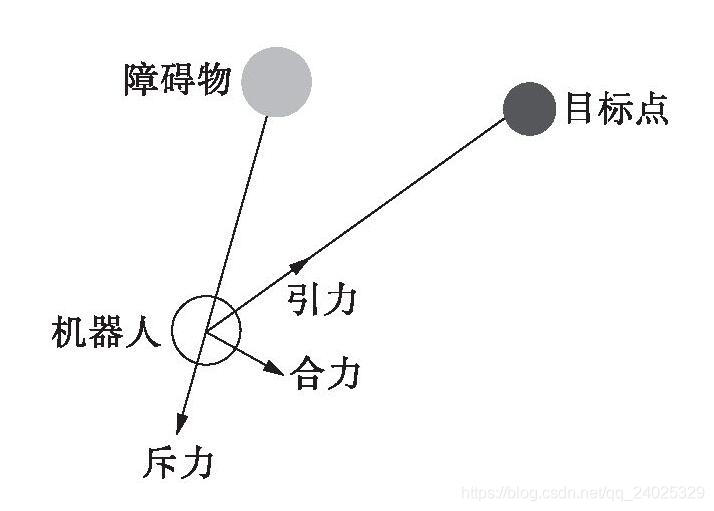
图1:传统人工势场示意图
三、带修正因子的Mamdani型模糊算法
Mamdani型模糊算法是一种模糊推理算法,由模糊化处理算子,模糊推理机制和非模糊化处理算子三个部分组成。Mamdani型模糊算法是通过事先掌握的一组推理规则实现从输入到输出的推理计算,从而建立准确的辨识系统。修正因子即在模糊算法的模糊规则里加入一个可以修改的因子,模糊规则与修正因子的关系一般为式(3-1)。
式(3-1)
本文的模糊控制算法采用双输入、单输出的形式,输入分别是斥力与引力的夹角,引力与斥力的差。输出为辅助力的大小。输入、输出的隶属函数全部采用5个三角形隶属度函数,见图(2)。模糊规则表见表(3-1)(修正因子=0.625)。反模糊化采用重心法。
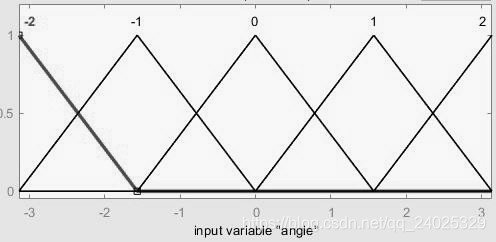
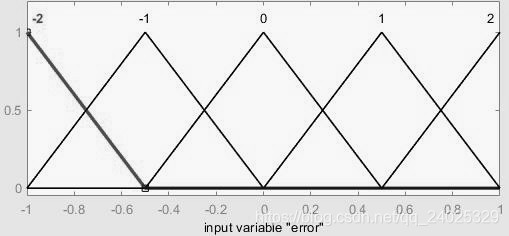
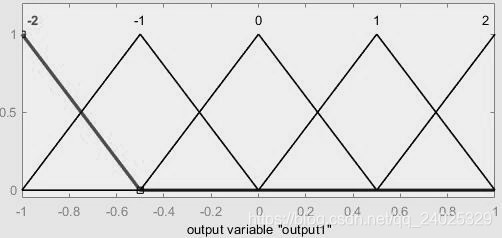
图2:模糊控制算法隶属度函数
| ANGLE | ||||||
|---|---|---|---|---|---|---|
| F | -2 | -1 | 0 | 1 | 2 | |
| -2 | -2 | -1 | -1 | 0 | 1 | |
| -1 | -2 | -1 | 0 | 0 | 1 | |
| 0 | -1 | -1 | 0 | 1 | 1 | |
| 1 | -1 | 0 | 0 | 1 | 2 | |
| 2 | -1 | 0 | 1 | 1 | 2 | |
表(3-1):模糊规则表
四、传统人工势场算法局部最优解的问题产生
图(3)是为传统人工势场算法的结果图,(第一个障碍物的坐标点为(1,1.3))。
图(3)
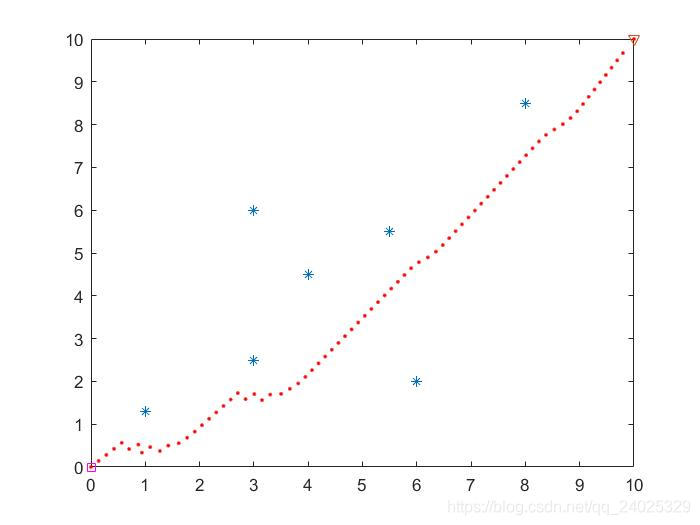
图3:传统人工势场算法
下面将第一个障碍物的坐标点修改为(1,1),此时便出现了局部最优解的问题,见图(4)
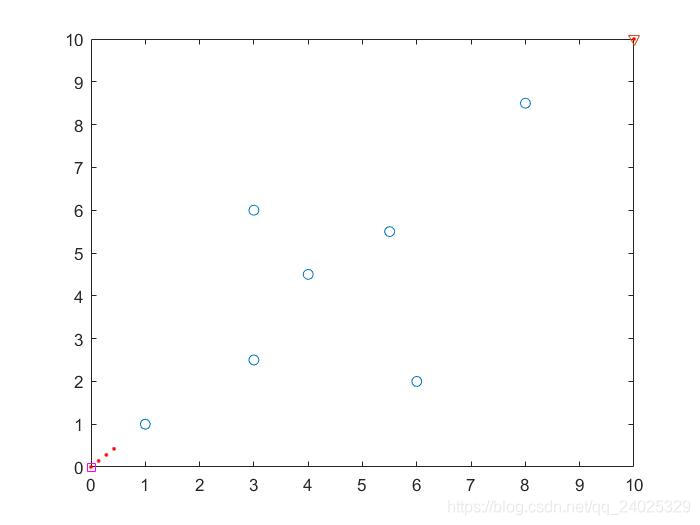
图4:传统人工势场算法
所以为了避免这种情况,需要在避障算法在遇到局部极小值时给机器人一个辅助的控制力,帮助机器人逃离极小值点,见图(5),而在一个复杂的环境中,障碍物的分布都具有随机性和不确定性,因为模糊算法在处理不确定的信息有很强的处理能力,所以采用模糊算法的输出作为辅助的控制力。
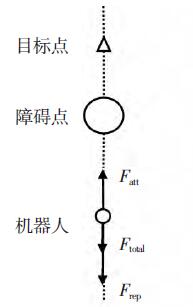
图5:受力示意图
五、不同的修正因子对算法的影响
(1)修正因子=0.8见图(6)
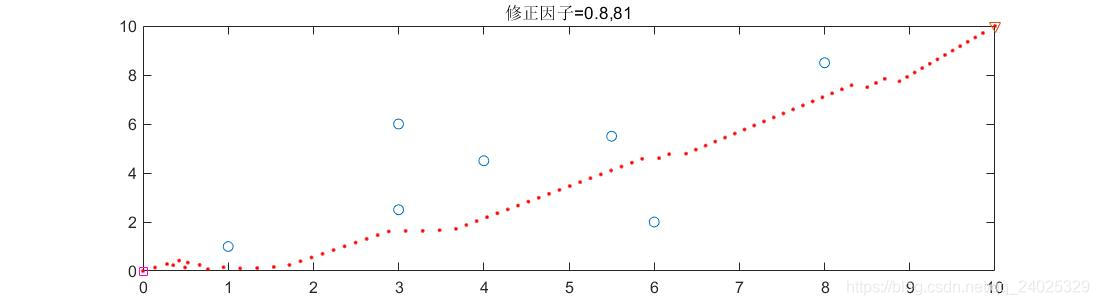
图6:所用步数为81步
(2)修正因子=0.625见图(7)
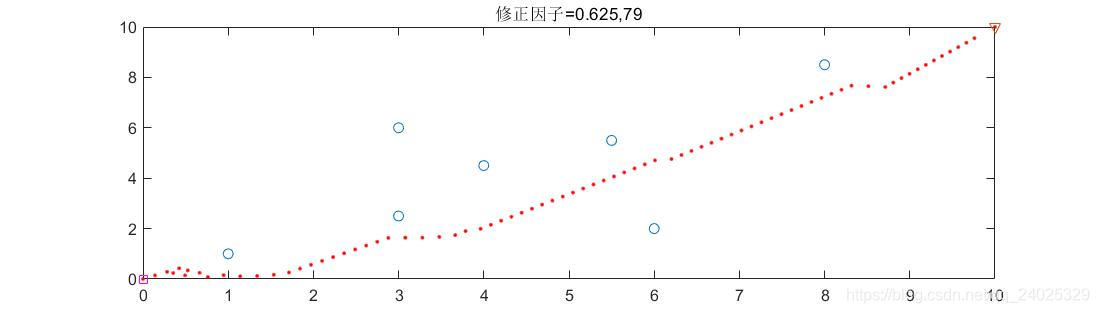
图7:所用步数为79步
(3)修正因子=0.45见图(8)
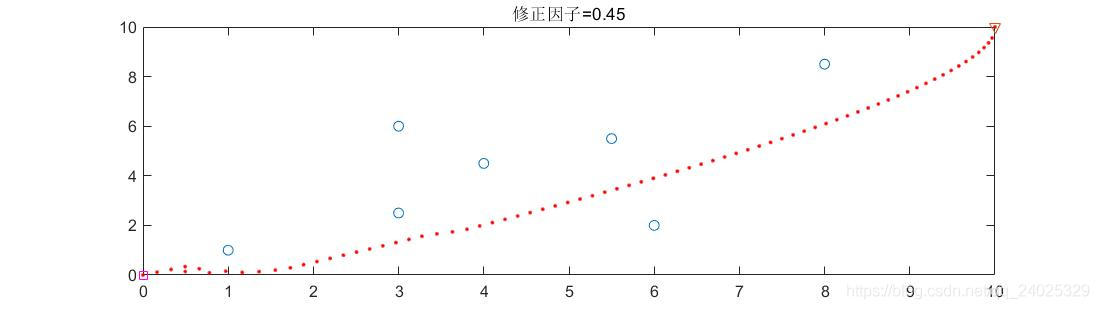
图8:所用步数为76步
六、结论
模糊控制算法对于不确定性、随机性比较强的环境处理能力非常出众。并且带有一个修正因子的Mamdani型模糊算法配合传统的人工势场算法能够适应多障碍复杂的环境,且可以安全避障,避障路径较为平滑。欢迎指正。
资料:
见:https://download.csdn.net/download/qq_24025329/10838135
含:模糊控制器.fis,人工势场算法.m



 浙公网安备 33010602011771号
浙公网安备 33010602011771号