毫米波传感简介（二）：调频连续波雷达—IF信号的相位

在本模块中，我们将探讨 IF 信号的相位，其对物体的极小位移非常敏感。雷达也正是凭此非常快速且准确地测量物体的速度。另外，这也是在心跳监测和振动检测等应用中使用雷达的基础。

1.傅里叶变换的快速回顾

时域中的正弦波会在频域中产生一个尖峰，该尖峰的位置与正弦波的频率相对应。傅里叶变换的一条重要性质是，峰值的相位对应于正弦波的初始相位，粗略证明如下(以正弦信号为例)：

\[\mathscr{F}[\sin(2\pi f_{0}t)]=\frac{1}{2j}[\delta(f-f_{0})-\delta(f+f_{0})] \tag{a} \]

\[\mathscr{F}\{\sin[2\pi f_{0}(t+t_{0})]\}=\frac{1}{2j}[\delta(f-f_{0})-\delta(f+f_{0})]e^{j\color{red}{2\pi f t_{0}}}\tag{b} \]

\[\sin[2\pi f_{0}(t+t_{0})] = \sin[2\pi f_{0}t+\color{red}{2\pi f_{0}t_0}]=\sin[2\pi f_{0}t+\color{red}{\phi_{0}}]\tag{c} \]

(a)式表明正弦信号的傅里叶变换的峰值出现在\(f=f_{0}\)处，将此结果带入(b)式可知带相位的正弦函数的傅里叶变换的峰值出的相位为\(2\pi f_{0}t_{0}\)，该相位恰好就是正弦信号的初始相位（见(c)式）。

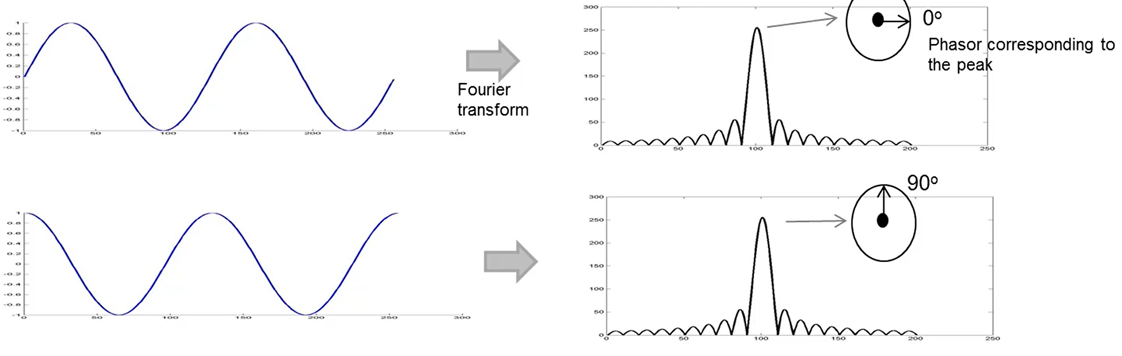
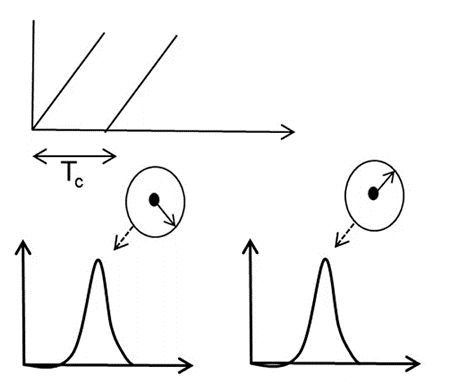
上图的示例中，上面的正弦波以特定的初始相位开始，该相位反映在其傅里叶变换的峰值相位中；下面正弦波的频率与上面的正弦波相同，但起始相位与上面的相位相差 90 度，因此，相应地，其傅里叶变换将在同样的位置有一个峰值，但相位与该前一个峰值相比偏移了90 度。

2.IF信号的相位

在毫米波传感简介（二）：调频连续波雷达—距离估计中我们已经知道，中频信号是一个单音信号，其频率仅与物体和雷达的距离有关。IF信号的相位则是发射脉冲的相位与接收脉冲的相位差。

\[s_{IF}(t) = A\sin(2\pi ft+\phi), \quad f=\frac{S2d}{c}, \quad \phi=\phi_{TX}-\phi_{RX}\tag{1} \]

其波形示意图如下：

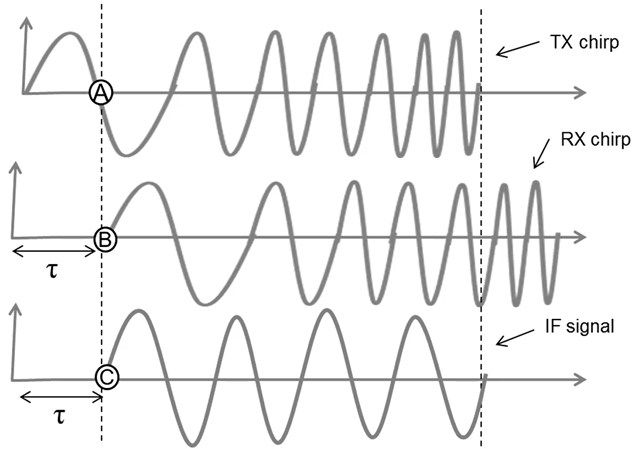
如果我们将物体远离雷达一段非常小的距离，相应的接收信号以及中频信号的波形将会变成下图中的蓝色曲线：

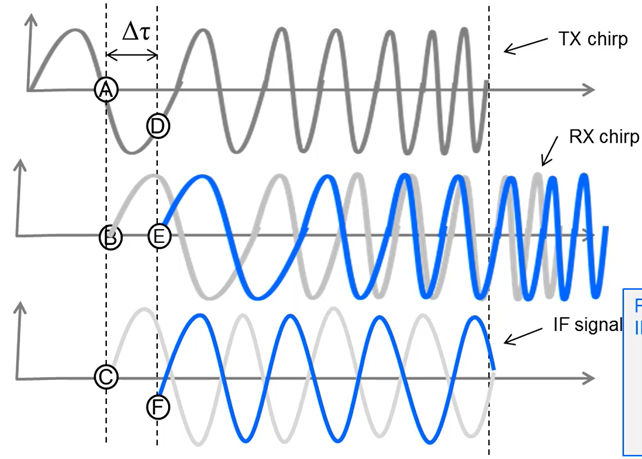
考虑移动前后，TX chirp，RX chirp和 IF signal信号发生了什么变化？

对于TX chirp，未移动时，接收端应该在A点对应的时间接收到反射信号，但是移动后，由于物体与雷达的距离增加了\(\Delta d\)，接收端应该会晚一些接收到信号，假设在D点对应的时间接收到信号，那么A,D两点之间的相位变化了多少？其实物体远离雷达\(\Delta d\)的距离，会导致接收端延迟\(\Delta \tau=2\Delta d/c\)接收到反射信号，那么显然A,D两点之间的相位变化为：

\[\phi_{D}-\phi_{A} = 2\pi f_{c}\Delta t = 2\pi f_{c}\cdot \frac{2\Delta d}{c}=\frac{4\pi \Delta d}{\lambda}\tag{2} \]

其中\(f_{c}\)为载波频率。

对于 RX chirp 本来应该在B点对应的时间接收到反射信号，但是由于物体的移动，变成了E点对应的时间接收到反射信号，那么显然B点出对应的接收信号的相位应该与E点处对应的接收信号的相位：

\[\phi_{E}=\phi_{B}\tag{3} \]

对于 IF signal 未移动时的相位为：\(\phi_{C}=\phi_{A}-\phi_{B}\)，移动后的相位为：\(\phi_{F}=\phi_{D}-\phi_{E}\)。由此可以得到移动前后 IF signal 的相位变化为：

\[\phi_{F}-\phi_{C}=\phi_{D}-\phi_{E} - \phi_{A} + \phi_{B}\tag{4} \]

将(2),(3)带入(4)式可以得到：

\[\phi_{F}-\phi_{C} = \phi_{D}-\phi_{A} = \frac{4\pi \Delta d}{\lambda}\tag{5} \]

至此，我们建立了IF信号的相位变化与距离变化之间的线性关系：

\[\Delta\phi = \frac{4\pi \Delta d}{\lambda}\tag{6} \]

你可能会担心，物体的移动也会导致中频信号频率的变化，但是其实不用担心，我们现在考虑的是非常小的移动距离，其远远小于距离分辨率。比如下面的示例：

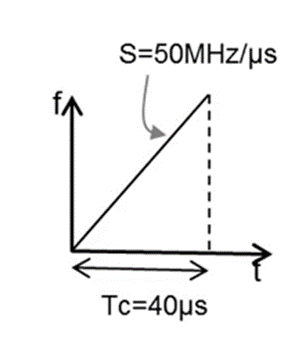
这是一个运行在77GHz频率的雷达的载波频率随时间变化的示意图，如果物体移动了1mm，我们分别观察中频信号的相位与频率变化：

• 相位变化：

\[1\text{mm}=\lambda/4\rightarrow \Delta\phi = \frac{4\pi \Delta d}{\lambda}=\pi=180^{0} \]

• 频率变化

\[\Delta f = \frac{S2\Delta d}{c} = 333\text{Hz} \]

这个频率变化看起来很大，但是在观察窗口\(T_{c}\)中，其只相当于\(\Delta f T_{c} = 0.013\)个周期。因此这种改变在IF信号的频谱中完全不可识别。

从上述示例可以看出，IF信号的相位对微小的物体移动非常敏感，但是其频率对微小的物体移动不敏感。

3. 利用两个调频连续波测量物体的速度

发射两个间隔时间为 \(T_{c}\) 的线性调频脉冲。与其中每个线性调频脉冲相对应的“range FFT”将在相同的位置具有峰值，但是具有不同的相位。这两个峰值的相位之间的测量相位差\(\omega\)将与物体的运动直接对应：

请注意，如果物体的速度为 v，则该物体在此时间段 \(T_{c}\) 内的移动距离将为 \(vT_{c}\)，由此可以得到：

\[\omega = \frac{4\pi vT_{c}}{\lambda}\Rightarrow v = \frac{\lambda\omega}{4\pi T_{c}}\tag{7} \]

也就是说：两个连续的线性调频脉冲之间测量的相位差可用于估算物体的速度。除速度测量之外，IF 信号的相位对微小移动非常敏感的事实也是一些趣应用的基础，如电机振动监测、心跳监测等。

4. 测量振动物体

下图描述了以振荡方式移动的物体随时间演变的过程。

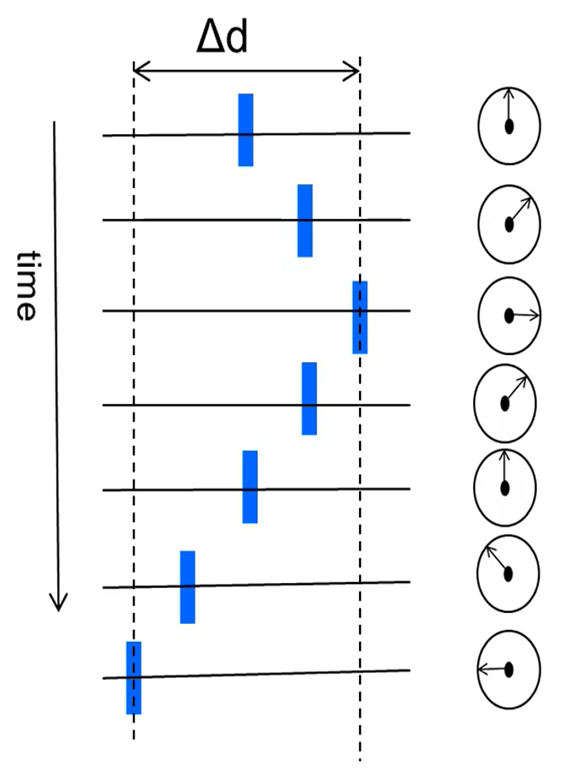
此物体从起始位置逐渐向右偏移，然后再返回，依此类推。这可以表示一个正在振荡的物体。在这里，我们假设这些移动非常微小，因此物体的最大位移 \(\Delta d\) 是波长的一小部分，例如一毫米或更短。
现在，如果我们将一个雷达放置在该振荡的物体前方并发射一系列等间隔的线性调频脉冲，会怎么样？

每个 TX 线性调频脉冲会产生一个反射线性调频脉冲，并且经处理的 IF 信号会在 "range-FFT" 中产生一个峰值。该峰值的频率不会在线性调频脉冲之间改变太多，因为Δd 非常小。但峰值的相位将会响应该物体的振荡移动。下图显示的就是相关情况：

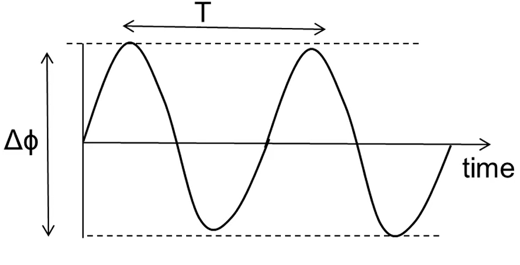
相位以特定的值开始，并将物体的移动映射到相位的变化，当物体返回时，相位返回到其初始值。可以通过查看该图了解很多信息:

• 最大相位偏移\(\Delta\phi\) 与最大位移 \(\Delta d\) （振幅）相关，如下所示：

\[\Delta f = \frac{4\pi \Delta d}{\lambda } \rightarrow \Delta d = \frac{\lambda\Delta\phi}{4\pi} \]

• 上图的周期性直接为我提供振动的周期。

所以，"range-FFT" 峰值相位随时间的演变可用于估算振动的振幅和周期。