调制信号的功率谱可以帮助我们确定调制方式所需要的传输带宽以及带宽效率。
线性调制信号中(包括作为特例的ASK,PSK和QAM),已调信号的等效低通为
\[v_{l}(t)=\sum_{n=-\infty}^{\infty}I_{n}g(t-nT)\tag{1.1}
\]
其中\(I_{n}\)为携带数字信息的平稳随机序列,\(g(t)\)为基本的调制脉冲。根据维纳-辛钦定理,欲求随机信号功率谱密度需先求自相关函数。
\[\begin{aligned}
R_{v_{l}}(t+\tau,t)&=E[v_{l}(t+\tau)v_{l}^{*}(t)]\\
&=E\left[\sum_{n=-\infty}^{\infty}\sum_{m=-\infty}^{\infty}I_{n}g(t+\tau-nT)I_{m}^{*}g^{*}(t-mT)\right]\\
&=\sum_{n=-\infty}^{\infty}\sum_{m=-\infty}^{\infty}E[I_{n}I_{m}^{*}]g(t+\tau-nT)g^{*}(t-mT)\\
&=\sum_{n=-\infty}^{\infty}\sum_{m=-\infty}^{\infty}R_{I}(n-m)g(t+\tau-nT)g^{*}(t-mT)
\end{aligned}
\tag{1.2}
\]
由于调制信号是每个符号周期T发送一次,每个周期内\(I_{n}\)的统计特性是一样的,所以\(v_{l}(t)\)是循环平稳随机过程,需要对其自相关函数取时间平均进而求取平均功率谱密度:
\[\begin{aligned}
\overline{R}_{v_{l}}(t+\tau,t)&=\overline{R}_{v_{l}}(\tau)=\frac{1}{T}\int_{0}^{T}R_{v_{l}}(t+\tau,t)dt\\
&=\frac{1}{T}\int_{0}^{T}\left(\sum_{n=-\infty}^{\infty}\sum_{m=-\infty}^{\infty}R_{I}(n-m)g(t+\tau-nT)g^{*}(t-mT)\right)dt\\
&\overset{k=n-m}{=}\frac{1}{T}\int_{0}^{T}\left(\sum_{k=-\infty}^{\infty}\sum_{m=-\infty}^{\infty}R_{I}(k)g(t+\tau-mT-kT)g^{*}(t-mT)\right)dt\\
&=\frac{1}{T}\sum_{k=-\infty}^{\infty}\sum_{m=-\infty}^{\infty}\int_{0}^{T}R_{I}(k)g(t+\tau-mT-kT)g^{*}(t-mT)dt\\
&=\frac{1}{T}\sum_{k=-\infty}^{\infty}R_{I}(k)\sum_{m=-\infty}^{\infty}\int_{0}^{T}g(t+\tau-mT-kT)g^{*}(t-mT)dt\\
&\overset{u=t-mT}{=}\frac{1}{T}\sum_{k=-\infty}^{\infty}R_{I}(k)\sum_{m=-\infty}^{\infty}\int_{-mT}^{-(m-1)T}g(u+\tau-kT)g^{*}(u)du\\
&=\frac{1}{T}\sum_{k=-\infty}^{\infty}\color{red}{R_{I}(k)\int_{-\infty}^{\infty}g(u+\tau-kT)g^{*}(u)du}\\
&=\frac{1}{T}\sum_{k=-\infty}^{\infty}\color{red}{g_{k}(\tau-kT)}
\end{aligned}
\tag{1.3}\]
其中
\[g_{k}(\tau)=R_{I}(k)\int_{-\infty}^{\infty}g(u+\tau)g^{*}(u)du\tag{1.4}
\]
对1.3式进行傅里叶变换即可得到\(v_{l}(t)\)的平均功率谱密度。
\[\begin{aligned}
\overline{S}_{v_{l}}(f)&=\mathscr{F}\left[\frac{1}{T}\sum_{k=-\infty}^{\infty}\color{red}{g_{k}(\tau-kT)}\right]\\
&=\frac{1}{T}\sum_{k=-\infty}^{\infty}G_{k}(f)e^{-j2\pi fkT}
\end{aligned}
\tag{1.5}
\]
其中\(G_{k}(f)\)为\(g_{k}(\tau)\)的傅里叶变换,如下:
\[\begin{aligned}
G_{k}(f)&=\mathscr{F}[g_{k}(\tau)]\\
&=\int_{-\infty}^{\infty}\left(R_{I}(k)\int_{-\infty}^{\infty}g(u+\tau)g^{*}(u)du\right)e^{-j2\pi f\tau}d\tau\\
&=R_{I}(k)\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}g(u+\tau)g^{*}(u)e^{-j2\pi f\tau}dud\tau\\
&\overset{v=u+\tau}{=}R_{I}(k)\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}g(v)g^{*}(u)e^{-j2\pi f(v-u)}dudv\\
&=R_{I}(k)\int_{-\infty}^{\infty}g(v)e^{-j2\pi fv}dv\int_{-\infty}^{\infty}g^{*}(u)e^{j2\pi fu}du\\
&=R_{I}(k)\int_{-\infty}^{\infty}g(v)e^{-j2\pi fv}dv\left(\int_{-\infty}^{\infty}g(u)e^{-j2\pi fu}du\right)^{*}\\
&=R_{I}(k)|G(f)|^{2}
\end{aligned}
\tag{1.6}
\]
其中\(G(f)\)为基本调制脉冲\(g(t)\)的傅里叶变换。将式(1.6)带入式(1.5)可以得到
\[\begin{aligned}
\overline{S}_{v_{l}}(f)&=\frac{1}{T}\sum_{k=-\infty}^{\infty}G_{k}(f)e^{-j2\pi fkT}\\
&=\frac{1}{T}\sum_{k=-\infty}^{\infty}R_{I}(k)|G(f)|^{2}e^{-j2\pi fkT}\\
&=\frac{1}{T}\left(\color{red}{\sum_{k=-\infty}^{\infty}R_{I}(k)e^{-j2\pi fkT}}\right)|G(f)|^{2}\\
&=\frac{1}{T}|G(f)|^{2}\color{red}{S_{I}(f)}
\end{aligned}
\tag{1.7}
\]
其中
\[S_{I}(f)=\sum_{k=-\infty}^{\infty}R_{I}(k)e^{-j2\pi fkT}\tag{1.8}
\]
这正是离散时间随机过程\(I_{n}\)的自相关函数的离散傅里叶变换,表示离散时间随机过程的功率谱密度。至此,我们得到了线性调制信号的功率谱密度如式(1.7)所示。该式表明线性调制信号的功率谱密度的形状由两个因素决定,一为调制使用的基本脉冲形状,二为信息序列\(I_{n}\)的功率谱密度。
基本脉冲形状对已调信号功率谱的形状有重要影响,较平滑的脉冲导致更紧凑的功率谱密度;信息序列\(I_{n}\)的功率谱密度取决于信息序列的相关特性。
例1:
假设输入数据\(I_{n}\)是实数并且相互独立,那么
\[R_{I}(k)=E[I_{n+k}I_{n}^{*}]=E[I_{n+k}I_{n}]
\]
当\(k\ne 0\)时,由于相互独立\(R_{I}(k)=E[I_{n+k}I_{n}]=E[I_{n+k}]E[I_{n}]=\mu_{I}^{2}\),其中\(\mu_{I}\)表示\(I_{n}\)的均值;
当\(k=0\)时,\(R_{I}(k)=E[I_{n+k}I_{n}]=E[I_{n}^{2}]=\sigma_{I}^{2}+\mu_{I}^{2}\),其中\(\sigma_{I}\)表示\(I_{n}\)的方差;
因此可得:
\[R_{I}(k) = \left \{ \begin{aligned} &\sigma_{I}^{2}+\mu_{I}^{2}, \quad & k=0\\ &\mu_{I}^{2}, \quad & k\ne 0\end{aligned} \right.
\]
带入(1.8)式可得:
\[\begin{aligned}
S_{I}(f) &= \sum_{k=-\infty}^{\infty}R_{I}(k)e^{-j2\pi fkT}\\
&=\sigma_{I}^{2}+\mu_{I}^{2}\sum_{k=-\infty}^{\infty}e^{-j2\pi fkT}\\
&=\sigma_{I}^{2}+\mu_{I}^{2}\left(\color{red}{\frac{1}{T}\sum_{k=-\infty}^{\infty}\delta(f-\frac{k}{T})}\right)\\
&=\sigma_{I}^{2}+\frac{\mu_{I}^{2}}{T}\sum_{k=-\infty}^{\infty}\delta(f-\frac{k}{T})
\end{aligned}\]
上式中红色部分使用了泊松求和公式。由此可以得到该线性调制信号的功率谱密度为:
\[\begin{aligned}
\overline{S}_{v_{l}}(f) &= \frac{1}{T}S_{I}(f)|G(f)|^{2}\\
&=\underbrace{\frac{\sigma_{I}^{2}}{T}|G(f)|^{2}}_{\text{continuous}}+\underbrace{\frac{\mu_{I}^{2}}{T^{2}}|G(f)|^{2}\sum_{k=-\infty}^{\infty}\delta(f-\frac{k}{T})}_{\text{discrete}}
\end{aligned}\]
观察上式我们会有两个发现:
- 当输入数据具有零均值时,离散谱就会变为零。这是数字传输中经常做的;
- 当输入数据具有零均值时,功率谱密度由\(G(f)\)决定;
例2:
在例1的基础上,假设调制使用的基本脉冲\(g(t)\)为矩形脉冲:
\[g(t) = A[u(t)-u(t-T)]
\]
其傅里叶变换为:
\[G(f) = AT\text{sinc}(fT)e^{-j\pi fT} \Rightarrow |G(f)|^{2}=A^{2}T^{2}\text{sinc}(fT)
\]
![]()
从而有:
\[\begin{aligned}
\overline{S}_{v_{l}}(f) &= \frac{\sigma_{I}^{2}}{T}A^{2}T^{2}\text{sinc}(fT)+\frac{\mu_{I}^{2}}{T^{2}}A^{2}T^{2}\text{sinc}(fT)\sum_{k=-\infty}^{\infty}\delta(f-\frac{k}{T})\\
&=\sigma_{I}^{2}A^{2}T\text{sinc}(fT) + \mu_{I}^{2}A^{2}\delta(f)
\end{aligned}\]
例3:
在例1的基础上,假设调制使用的基本脉冲\(g(t)\)为升余弦脉冲:
\[g(t) = \frac{A}{2}\left[1+\cos\left(\frac{2\pi}{T}(t-\frac{T}{2})\right)\right][u(t)-u(t-T)]
\]
其傅里叶变换为:
\[G(f) = \frac{AT}{2}\text{sinc}(fT)\frac{1}{1-f^{2}T^{2}}e^{-j\pi fT}
\]
![]()
从而有:
\[\begin{aligned}
\overline{S}_{v_{l}}(f) &= \frac{\sigma_{I}^{2}}{T}|G(f)|^{2}+\frac{\mu_{I}^{2}}{T^{2}}|G(f)|^{2}\sum_{k=-\infty}^{\infty}\delta(f-\frac{k}{T})\\
&=\frac{\sigma_{I}^{2}A^{2}T\text{sinc}(fT)}{4(1-f^{2}T^{2})^{2}}+\frac{\mu_{I}^{2}A^{2}}{4}\delta(f)+\frac{\mu_{I}^{2}A^{2}}{16}\delta(f-\frac{1}{T})+\frac{\mu_{I}^{2}A^{2}}{16}\delta(f+\frac{1}{T})
\end{aligned}\]
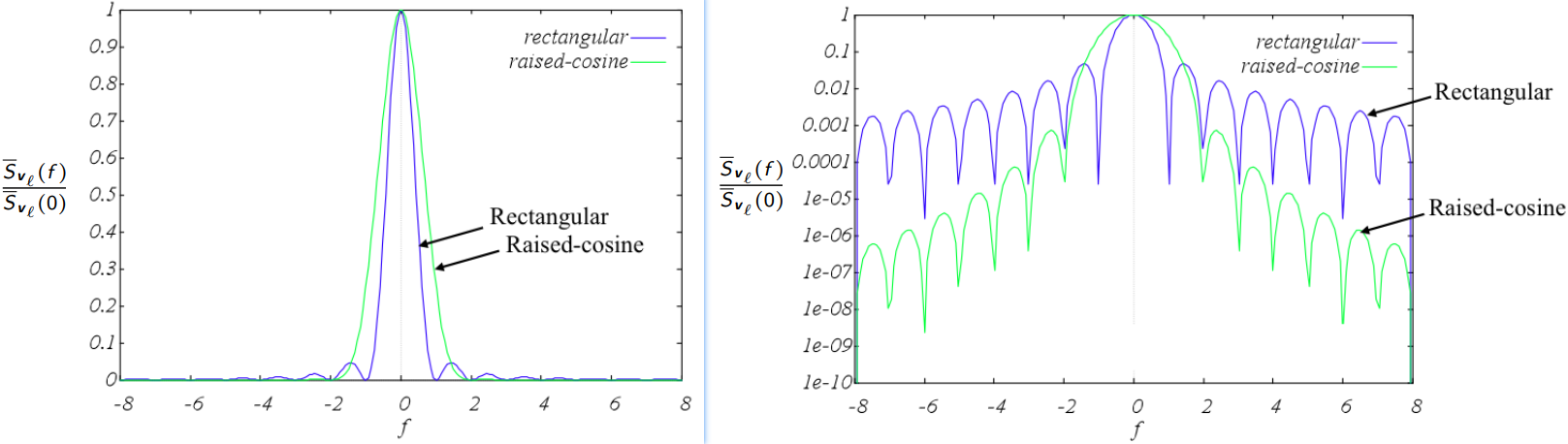
令\(A=T=\sigma_{I}^{2}=1,\mu_{I}=0\),并对比例2,例3的平均功率谱密度
![]()
平滑的基本脉冲,占据更宽的主瓣带宽,但是旁瓣衰减更快,从到导致更高的带宽效率。可以发现,升余弦基本脉冲比矩形脉冲具有更高的带宽效率。
预编码谱成形
控制已调信号功率谱密度的一种方法是通过控制信息序列的相关特性,其做法是将信息序列通过一个可逆滤波器,该滤波器控制已调信号的相关特性,因为它是可逆的,所以原始信息序列可由此恢复。这种技术称为预编码谱成形(Spectral Shaping by Precoding)。
例如,使用的预编码为\(J_{n}=I_{n}+\alpha I_{n-1}\),通过改变\(\alpha\)值就能控制已调信号波形的功率谱密度。一般,引入一个长度为L的记忆,预编码的形式为
\[J_{n}=\sum_{k=0}^{L}\alpha_{k}I_{n-k}\tag{1.9}
\]
然后,产生已调波形
\[v_{l}(t)=\sum_{k=-\infty}^{\infty}J_{k}g(t-kT)\tag{1.10}
\]
因为预编码运算是线性运算,结果功率谱密度为
\[S_{v_{l}}=\frac{1}{T}|G(f)|^{2}|\sum_{k=0}^{L}\alpha_{k}e^{-j2\pi kfT}|^{2}S_{I}(f)\tag{1.11}
\]
改变\(\alpha_{k}\)值可以控制功率谱密度。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号