正交幅度调制(QAM)

将来自信息序列$\{a_n\}$的两个分离的k比特符号同时加在两个正交载波$\cos2\pi f_{c}t$和$\sin2\pi f_{c}t$上。这就是正交幅度调制(Quadrature Amplitude Modulation,QAM)。信号波形可以表示为：

$$\begin{aligned} s_{m}(t) &= \text{Re}[(A_{mi}+jA_{mq})g(t)e^{j2\pi f_{c}t}]\\ &=A_{mi}\color{red}{g(t)\cos(2\pi f_{c}t)}-A_{mq}\color{red}{g(t)\sin(2\pi f_{c}t)}\\ &=A_{mi}\color{red}{y_{1}(t)}-A_{mq}\color{red}{y_{2}(t)} \end{aligned}\tag{1}$$

• $A_{mi},A_{mq}$是承载信息的正交载波的信号幅度；
• $g(t)$为实信号脉冲

1.正交展开

由(1)式最后两行可以看出，$s_{m}(t)$被表示成了两个基函数$\color{blue}{y_{1}(t)=g(t)\cos(2\pi f_{c}t), y_{2}(t)=-g(t)\sin(2\pi f_{c}t)}$的线性组合，其中的系数分别为$\color{blue}{A_{mi},A_{mq}}$。这两个基函数与相位调制中的两个基函数完全一样，因此可以得到完全一样的标准正交基如下：

$$\begin{aligned} \phi_{1}(t) &= \sqrt{\frac{2}{\mathcal{E}_{g}}}g(t)\cos(2\pi f_{c}t)\\ \phi_{2}(t) &= -\sqrt{\frac{2}{\mathcal{E}_{g}}}g(t)\sin(2\pi f_{c}t) \end{aligned}\tag{2}$$

将(1)式进行改写并将(2)式带入可以得到：

$$\begin{aligned} s_{m}(t) &= A_{mi}\sqrt{\frac{\mathcal{E}_{g}}{2}}\color{red}{\sqrt{\frac{2}{\mathcal{E}_{g}}}g(t)\cos(2\pi f_{c}t)}+A_{mq}\sqrt{\frac{\mathcal{E}_{g}}{2}}\color{red}{\left(-\sqrt{\frac{2}{\mathcal{E}_{g}}}g(t)\sin(2\pi f_{c}t)\right)}\\ &=A_{mi}\sqrt{\frac{\mathcal{E}_{g}}{2}}\color{red}{\phi_{1}(t)}+A_{mq}\sqrt{\frac{\mathcal{E}_{g}}{2}}\color{red}{\phi_{2}(t)} \end{aligned}\tag{3}$$

此即为QAM调制信号的正交展开式，相应的矢量表达式为：

$$\begin{aligned} \bold{s_{m}}=\left[A_{mi}\sqrt{\frac{\mathcal{E}_{g}}{2}},A_{mq}\sqrt{\frac{\mathcal{E}_{g}}{2}}\right] \end{aligned}\tag{4}$$

2. 能量计算

信号$s_{m}(t)$的能量为

$$\begin{aligned} \mathcal{E}_{m}=\Vert \bold{s_{m}} \Vert^{2}=\frac{\mathcal{E}_{g}}{2}(A_{mi}^{2}+A_{mq}^{2}) \end{aligned} \tag{5}$$

在矩形星座的特殊条件下，即$M=4,16,64\cdots$且在两个方向上的幅度为$\pm1,\pm3,\cdots,\pm(\sqrt{M-1})$，平均信号能量为：

$$\begin{aligned} \mathcal{E}_{avg}&=\frac{1}{M}\frac{\mathcal{E}_{g}}{2}\sum_{m=1}^{\sqrt{M}}\sum_{n=1}^{\sqrt{M}}(A_{m}^{2}+A_{n}^{2})\\ &=\frac{\mathcal{E}_{g}}{2M}\times\frac{2M(M-1)}{3}\\ &=\frac{M-1}{3}\mathcal{E}_{g} \end{aligned} \tag{6}$$

平均比特信号能量为：

$$\mathcal{E}_{bavg} = \frac{M-1}{3\log_{2}{M}}\mathcal{E}_{g}\tag{7}$$

3. 信号点距离

任意一对信号点之间的距离为

$$\begin{aligned}d_{mn}&=\sqrt{\Vert \bold{s_{m}-s_{n}}\Vert^{2}}\\ &=\sqrt{\frac{\mathcal{E}_{g}}{2}[(A_{mi}-A_{ni})^{2}+(A_{mq}-A_{nq})^{2}]} \end{aligned}\tag{8}$$

当两个信号点相邻时，距离最短，可以得到：

$$d_{\min}=\sqrt{\frac{\mathcal{E}_{g}}{2}[(0)^{2}+(2)^{2}]}=\sqrt{2\mathcal{E}_{g}}\tag{9}$$

由(7)式可以得到：

$$\mathcal{E}_{g}=\frac{3\log_{2}{M}}{M-1}\mathcal{E}_{bavg}$$

将其带入(9)式可以得到最小距离与平均比特信号能量的关系：

$$d_{\min}=\sqrt{\frac{6\log_{2}M}{M-1}\mathcal{E}_{bavg}}\tag{10}$$

4. QAM的另一种表示

对(1)式进行改写

$$\begin{aligned} s_{m}(t) &= \text{Re}[(A_{mi}+jA_{mq})g(t)e^{j2\pi f_{c}t}]\\ &=\text{Re}[\color{red}{r_{m}e^{j\theta_{m}}}g(t)e^{j2\pi f_{c}t}]\\ &=\color{red}{r_{m}}g(t)\cos(2\pi f_{c}t+\color{red}{\theta_{m}}) \end{aligned}\tag{11}$$

• $r_{m} = \sqrt{A_{mi}^{2}+A_{mq}^{2}}$
• $\theta_{m}=\tan^{-1}(A_{mq}/A_{mi})$
  从这个表达式可以看出，QAM信号波形可以看成组合幅度$r_{m}$和相位$\theta_{m}$的调制。可以选择$M_{1}$个电平的PAM和$M_{2}$个相位的PSK的任意组合来构成一个$M=M_{1}M_{2}$个星座点的PAM-PSK组合星座图。

5. PAM,PSK和QAM的通用形式

PAM信号的表达式为：

$$s_{m}(t)=\text{Re}[A_{m}g(t)e^{j2\pi f_{c}t}],\quad m=1,2,\cdots,M$$

PSK信号的表达式为：

$$s_{m}(t) = \text{Re}\left[g(t)e^{j\frac{2\pi}{M}(m-1)}e^{j2\pi f_{c}t}\right]=\text{Re}[A_{m}g(t)e^{j2\pi f_{c}t}],\quad m=1,2,\cdots,M$$

QAM信号的表达式为：

$$s_{m}(t)=\text{Re}[(A_{mi}+jA_{mq})g(t)e^{j2\pi f_{c}t}]=\text{Re}[A_{m}g(t)e^{j2\pi f_{c}t}], m=1,2,\cdots,M$$

可见PAM,PSK和QAM信号的通用形式为：

$$s_{m}(t) = \text{Re}[A_{m}g(t)e^{j2\pi f_{c}t}], m=1,2,\cdots,M\tag{12}$$

式中，$A_{m}$由信号传输方式确定

• PAM的$A_{m}$是实数，一般等于$\pm1,\pm3,\cdots,\pm(M-1)$
• M元PSK的$A_{m}$是复数，等于$e^{j\frac{2\pi}{M}(m-1)}$
• QAM的$A_{m}$也是复数，等于$A_{m}=A_{mi}+A_{mq}$

从这个意义上说，PAM,PSK和QAM属于同一种类型，PAM和PSK可认为QAM的特例。在QAM传输方式中，幅度和相位都携带信息，而PAM和PSK只是幅度或相位携带信息。

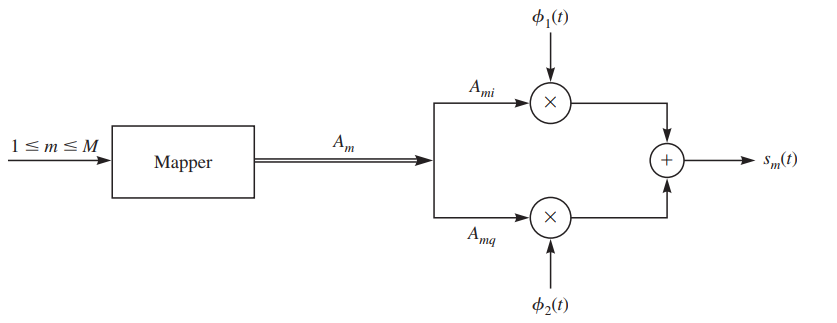
PAM,PSK和QAM信号的信号空间的维度是相当低的(PAM为一维，PSK和QAM为二维的)，并且与星座的大小M无关。下图所示就是这种一般类型信号传输方式调制器的结构，其中$\phi_{1}(t), \phi_{2}(t)$由式(2)确定。