pi/4范围内sinx，cosx查找表

目标：创建\([0,\pi/4]\)的\(\sin,\cos\)查找表，利用该查找表能够生成\([0,k*2\pi],k=1,2,\cdots\)内的所有值。查找表的大小为4点。

思路：
根据\([0,\pi/4]\)内的\(\sin x, \cos x\)的值，再结合

\[\begin{aligned}\cos(x)&=1*\cos(x)-0*\sin(x)\\ &=\sin(\pi/2)\cos(x)-\cos(\pi/2)\sin(x)\\ &=\sin(\pi/2-x),x\in[0,\pi/4] \end{aligned}\tag{1}\]

\[\begin{aligned}\sin(x)&=0*\cos(x)+1*\sin(x)\\ &=\cos(\pi/2)\cos(x)+\sin(\pi/2)\sin(x)\\ &=\cos(\pi/2-x),x\in[0,\pi/4] \end{aligned}\tag{2}\]

可以求得\([\pi/4,\pi/2]\)内的所有值，那么就可以得到\([0,\pi/2]\)范围内的所有\(\sin x, \cos x\)值。再进一步由于对称性可轻易得到\([0,2\pi]\)范围内的所有所有\(\sin x, \cos x\)值。对称性如下图1所示：

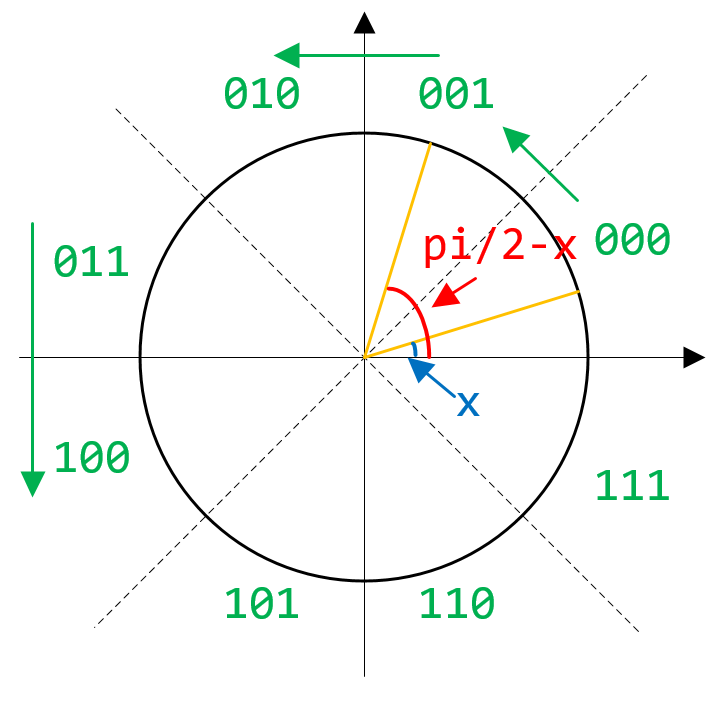
图1： 正、余弦函数的对称性

推导：
从图1可以看出\([0,2\pi]\)被划分为8个区域，每个区域4个点，那么要遍历8个区域，则需要32个点，所以查找表的索引位宽为5位。

那么如何根据\([0,\pi/4]\)的\(\sin x,\cos x\)的值，获得\([0，2\pi]\)区间内\(\sin x, \cos x\)的值呢？

见下图：

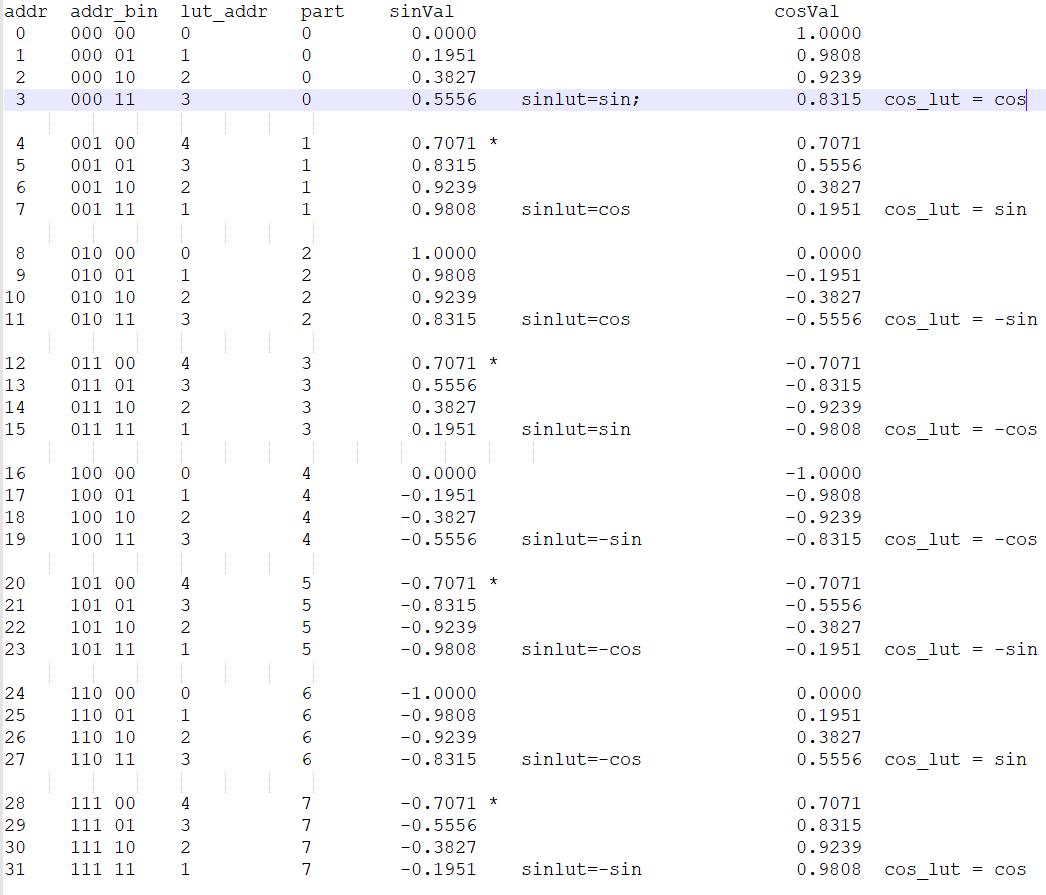
上图中lut_addr的最大值为4是因为查找表要取到\(\pi/4\)这个点。图中第第6列，第8列中的sinlut, coslut是指利用\([0,\pi/4]\)范围内的\(\sin,\cos\)查找表获得的\([0,2\pi]\)范围内的所有所有\(\sin x, \cos x\)值，而sin,cos则是指\([0,\pi/4]\)范围内的\(\sin,\cos\)的值。

注意：为了能够获得\(\pi/4\)这个点的值，查找表实际有5个点。第5个点的值就是\(\cos(\pi/4)=\sin(\pi/4)\)。

同理，可以获得更多点的\([0,\pi/4]\)范围内的\(\sin,\cos\)查找表。只需要将本文中的4点修改为16点，64点，256点等等。推广的同时要多取一点即\(\pi/4\)这个点的值。