带通信号的等效低通

1. 低通信号

信号的傅里叶变换提供了其频域信息。实信号\(x(t)\)的傅里叶变换具有厄米特(Hermitian)对称性，即\(X(-f)=X^{*}(f)\)，从而\(|X(-f)|=|X(f)|\)以及\(\angle{X^{*}(f)}=-\angle X(f)\)。也就是说，对于实信号\(x(t)\)，其傅里叶变换\(X(f)\)的幅度具有偶对称性而相位具有奇对称性。由于该对称性，有关信号的全部信息都包含在正（或负）频域中，由\(X(f)(f\ge 0)\)可以完整地重构\(x(t)\)。基于此观察，实信号\(x(t)\)的带宽是其频率支持集的一半。

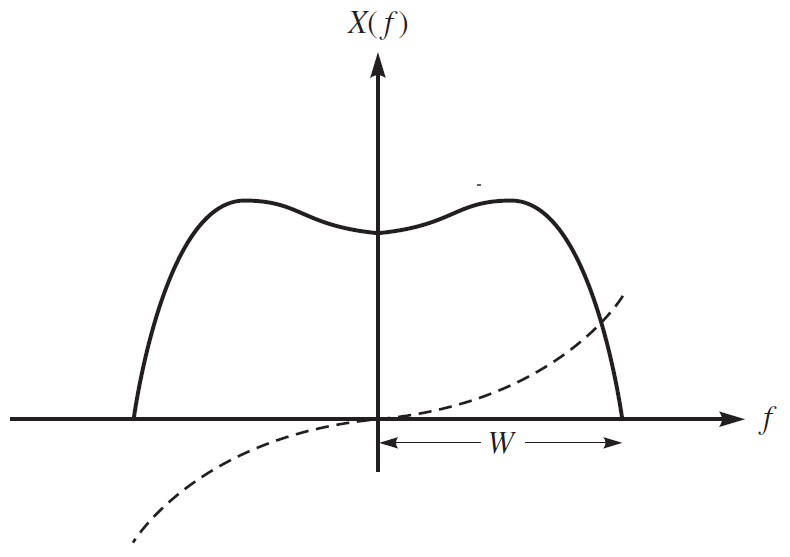
低通或基带信号是其频谱位于零频附近的信号，例如，语音，音乐和视频信号都是低通信号，虽然它们具有不同的频谱特性和带宽。通常，低通信号是低频信号，意即在时域它们是缓慢变化的信号，没有跳变或突变。实低通信号的带宽是最小的正频率\(W\)，在\([-W,W]\)之外\(X(f)=0\)。对这样的信号，频率支持（即\(X(f)\ne0\)的频谱范围）是\([-W,W]\)。图1所示为一实低通信号的谱的例子，实线表示幅度谱\(|X(f)|\)，虚线表示相位谱\(\angle{X(f)}\)。

图1 实低通（基带）信号的频谱

也可以定义一个信号的正频谱和负频谱为

\[X_{+}(f)= \left \{ \begin{aligned} &X(f), \quad &f>0 \\ &\frac{1}{2}X(0),\quad &f=0 \\ &0, \quad &f<0\end{aligned} \right. \qquad X_{-}(f)= \left \{ \begin{aligned} &X(f), \quad &f<0 \\ &\frac{1}{2}X(0),\quad &f=0 \\ &0, \quad &f>0\end{aligned} \right. \tag{1} \]

显然，\(X_{+}(f)=X(f)u_{-1}(f),X_{-}(f)=X(f)u_{-1}(-f)\)和\(X(f)=X_{+}(f)+X_{-}(f)\)。对于实信号\(x(t)\)，\(X(f)\)是厄米特的，则\(X_{-}(f)=X_{+}^{*}(f)\)。

对于复信号\(x(t)\)，其频谱是不对称的，因此该信号不能仅由正频率的信息来重构。对复信号，带宽定义为频谱为非零值的全部频率范围的一半，即该信号频率支持集的一半。该定义与实信号的带宽定义是一致的。根据该定义可以一般认为，对于所有的信号（实的或者复的），带宽定义为频率支持集的一半。

2. 带通信号

在实际中，信号的谱特性与通信信道并不总是匹配的，这就要求从许多不同调制方法中选择一种来调制信息信号，使其谱特性和信道的谱特性匹配。在该过程中，低通消息信号的谱变换为高频，结果已调信号为带通信号。

带通信号是一种实信号，其频率内容（或谱）位于远离零的某频率\(\pm f_{0}\)附近。更正式地将带通信号定义为在\(f_{0}\)存在且具有\(W\)的实信号，即仅在\([f_{0}-W/2,f_{0}+W/2]\)区间的\(X(f)\)的非零。显然带通信号\(x(t)\)的带宽最多等于\(W\)。

图2所示为带通信号频谱的一个例子。注意，因为信号\(x(t)\)是实的，其幅度谱是偶对称的，相位谱是奇对称的。同时中心频率\(f_{0}\)不必是带通信号频段的中间。由于谱的对称性，\(X_{+}(f)\)包含了重构\(X(f)\)所必要的全部信息，即

\[X(f) = X_{+}(f)+X_{-}(f)=X_{+}(f)+X_{+}^{*}(f) \tag{2} \]

该式表明完全可以由\(X_{+}(f)\)重构\(X(f)\)。

图2 实带通信号的频谱

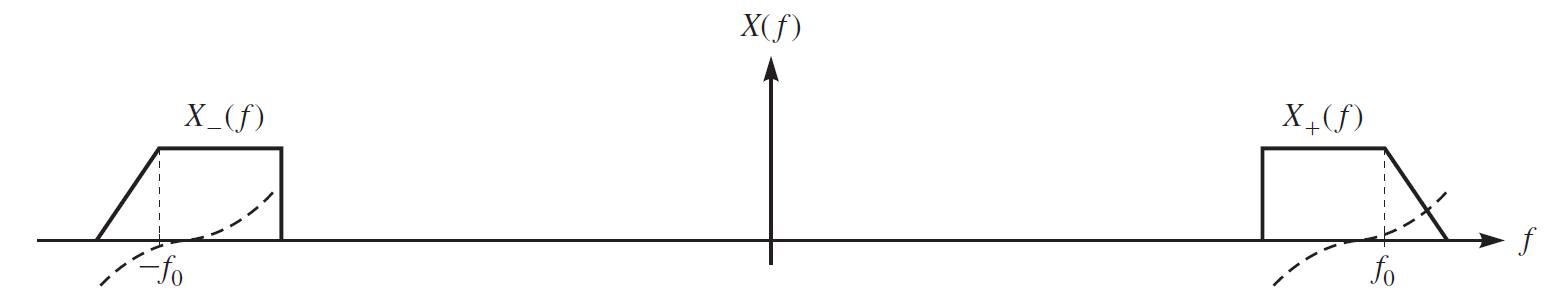
3. 低通信号表示带通信号

对于带通信号\(x(t)\)，其傅里叶变换为\(X(f)\)。将\(X(f)\)正半轴部分定义为\(X_{+}(f)\)，由\(X_{+}(f)\)通过傅里叶反变换得到的时域信号定义为\(x_{+}(t)\)（预包络）。那么：

\[\begin{aligned} x_{+}(t) &= \mathscr{F}^{-1}[X_{+}(f)] \\ &= \mathscr{F}^{-1}[{X(f)u(f)}] \\ &= x(t)\star(\frac{1}{2}\delta(t)+j\frac{1}{2\pi t}) \\ &= \frac{1}{2}x(t) +\frac{j}{2}\hat{x}(t) \end{aligned} \tag{3} \]

上式中利用了频域相乘等效于时域卷积的概念。同时频域阶跃函数\(u(f)\)的傅里叶反变换为\(\frac{1}{2}\delta(t)+j\frac{1}{2\pi t}\)（参见谁的傅里叶变换是阶跃函数？）。另外，\(\hat{x}(t)=\frac{1}{\pi t}\star x(t)\)表示\(x(t)\)的希尔伯特变换。

现在定义：\(x(t)\)的等效低通\(x_{l}(t)\)为由频谱\(2X_{+}(f+f_{0})\)确定的信号。 那么可以得到：

\[X_{l}(f)=2X_{+}(f+f_{0})u(f+f_{0})\tag{4} \]

结合前面带通信号的定义可以知道，\(x_{l}(t)\)的频谱位于零频附近，所以一般为复低通信号，该信号称为带通信号\(x(t)\)
的等效低通或复包络。那么利用傅里叶变换的频移特性可以得到：

\[\begin{aligned} x_{l}(t) &= \mathscr{F}^{-1}[X_{l}(f)] \\ &=2x_{+}(t)e^{-j2\pi f_{0}t} \\ &=(x(t)+j\hat{x}(x))e^{-j2\pi f_{0}t} \end{aligned} \tag{5} \]

于是可以得到

\[x(t) = Re[x_{l}(t)e^{-j2\pi f_{0}t}]\tag{6} \]

这就是带通信号的等效低通表示了。

总结一下得到等效低通的过程：根据带通信号频谱的对称性，截取一半，然后将频谱搬移下来，乘以2，再做个傅里叶反变换，得到等效低通的时域表达式。

那么如果我们得到等效低通的频域表达式为\(X_{l}(f)\)，通过逆推上面的过程就可以得到带通信号的频域表达式：

• 将\(X_{l}(f)\)向右搬移得到\(X_{l}(f-f_{0})\)
• 根据带通信号频谱的Hermitian对称性，将\(X_{l}(f)\)反转、取共轭，得到\(X_{l}^{*}(-f)\)
• 将反转、取共轭后的信号向左平移，得到\(X_{l}^{*}[-(f+f_{0})]=X_{l}^{*}(-f-f_{0})\)
• 推导等效低通的时候，进行了\(\times 2\)的操作，所以这里需要\(\times \frac{1}{2}\)
• 最终得到的结果为：

\[X(f)=\frac{1}{2}[X_{l}(f+f_{0})+X_{l}^{*}(-f-f_{0})]\tag{7} \]

等效低通信号通常为复数，将其写为实部加虚部的形式\(x_{l}(t)=x_{i}(t)+jx_{q}(t)\)并带入(5)式，可以得到：

\[[x_{i}(t)+jx_{q}(t)]=[x(t)+j\hat{x(t)}]e^{-j2\pi f_{c}t}\tag{8} \]

进一步可以得到：

\[[x_{i}(t)+jx_{q}(t)]e^{j2\pi f_{c}t}=[x(t)+j\hat{x}(t)]\tag{9} \]