累加器

累加运算

1. 累加原理

累加运算如式(1)所示：

\[s = \sum_{n=0}^{L-1}a_{n} \tag{1} \]

它表示N个数相加。累加运算由累加器实现，其实质是完成一系列的加法运算，但是与简单的加法运算不同，他需要将前一次运算的结果反馈至输入端，作为新一次加法运算的加数，如式(1)中，\(a_{1}\)和\(a_{2}\)相加的结果需要反馈回来与\(a_{3}\)相加。所以，累加器中具有反馈之路。此外，累加器最终输出的是累加结果，对于中间运算结果可不比输出。所以，累加器末端还需要一个捕获寄存器，捕获最终结果。累加器的工作原理是：每帧数据周期性地流动，新的数据不断进入累加器与反馈之路相加，实现累加，由捕获寄存器接收捕获信号，输出最终结果。

定义：构成一个累加结果的输入数据为一帧数据，一帧数据所包含的数据个数为帧长度。式（1）中，\(a_{0},a_{1},\cdots,a_{L-1}\)为一帧数据，帧长度为L。由加法运算可知，两个数相加会引起位增长。为保证累加结果的正确，必须使得中间运算结果有足够的位宽。假定输入数据位宽为B，那么最终结果的位宽为：

\[W_{s} = \text{ceil}(B+log_{2}L) \tag{2} \]

式中ceil表示向上取整。这就要求将输入数据以及中间运算结果进行符号位扩展，使位宽达到\(W_{s}\)。

2. 顺序累加器

数据流按帧顺序进入累加器，即第一帧数据进入求和，然后第二帧数据进入求和，以此类推，这样的累加器称为顺序累加器。整个数据依时间顺序流动，帧与帧之间没有间断。

图1. 顺序累加器数据流

假定有四帧数据，每帧长度均为4。第一帧数据为\(a_{1},a_{2},a_{3},a_{4}\)；第二帧数据为\(b_{1},b_{2},b_{3},b_{4}\)；第三帧数据为：\(c_{1},c_{2},c_{3},c_{4}\);第四帧数据为\(d_{1},d_{2},d_{3},d_{4}\)。这四帧数据的时间顺序如图1所示。现在要求对这四帧数据依次求和，最终输出\(s_{a},s_{b},s_{c},s_{d}\)，计算方式如式(3)~(6)所示。

\[s_{a} = a_{1} + a_{2} + a_{3} + a_{4} \tag{3} \]

\[s_{b} = b_{1} + b_{2} + b_{3} + b_{4} \tag{4} \]

\[s_{c} = c_{1} + c_{2} + c_{3} + c_{4} \tag{5} \]

\[s_{a} = d_{1} + d_{2} + d_{3} + d_{4} \tag{6} \]

根据累加器的原理可得如图2所示的顺序累加器硬件结构，包括加法器、流水寄存器和捕获寄存器。顾名思义，流水寄存器目的是使数据流动起来，以提高系统处理速度。捕获寄存器用于捕获最终期望结果。

图2. 顺序累加器硬件结构

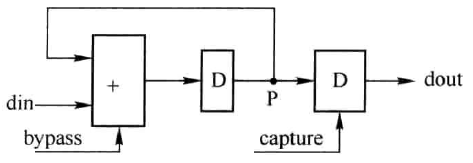
图2中，数据由din端进入，最终结果由dout端输出，整个时序如图3.16所示。从时序图中可以看出，bypass为“直通”信号，当其为高时，加法器输入端数据din直接通过加法器而不执行任何操作到加法器输出端，表明新一帧数据的开始；当其为低时，执行加法操作，将输入数据与反馈端数据相加，以便对新一帧数据求和。P节点数据反馈至加法器输入端与din相加求和，实现数据的累加，相应数据依次为\(a_{1},a_{1}+a_{2},a_{1}+a_{2},a_{1}+a_{2}+a_{3},s_{a}\)中间结果未显示。capture作为捕获信号，当其为高时，捕获P节点的数据并将其输出，否则保持输出不变，加法器的位宽由式\((2)\)决定。

图3. 顺序累加器时序图

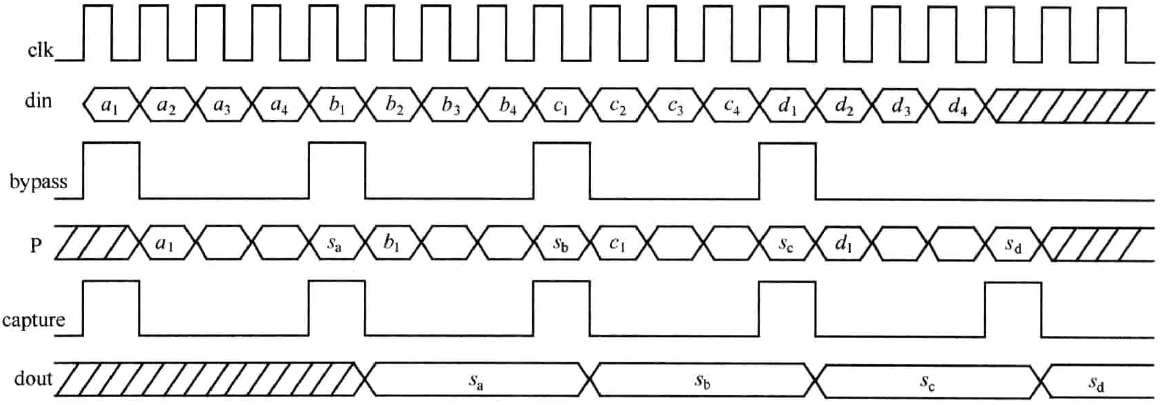
顺序累加器设计的关键是使数据流与各控制信号(bypass 和 capture)对应起来，实现正确累加。从图3可以看出，这并不难做到。bypass和capture两者周期一致且取决于数据帧长度。

3. 滑动累加器

滑动累加器是指数据流按帧交错顺序进入，此时，在计算每帧数据和时就要求对反馈支路数据进行滑动以实现正确累加。

假定有4帧数据，每帧长度均为4。第一帧数据为\(a_{1},b_{1},c_{1},d_{1}\)，第二帧数据为\(a_{2},b_{2},c_{2},d_{2}\)，第三帧数据为\(a_{3},b_{3},c_{3},d_{3}\)，第四帧数据为\(a_{4},b_{4},c_{4},d_{4}\)。这四帧数据的时间顺序与图1保持一致。显然，此时数据流的顺序是第一帧的第一个，第二帧的第一个，第三帧的第一个，第四帧的第一个，紧接着，第一帧的第二个，第二帧的第二个，依次类推。现在要求对这四帧数据依次求和，最终输出\(s_{1},s_{2},s_{3},s_{4}\)，如式(7)\(\sim\)(10)所示。

\[s_{1} = a_{1} + b_{1} + c_{1} + d_{1} \tag{7} \]

\[s_{2} = a_{2} + b_{2} + c_{2} + d_{2} \tag{8} \]

\[s_{3} = a_{3} + b_{3} + c_{3} + d_{3} \tag{9} \]

\[s_{4} = a_{4} + b_{4} + c_{4} + d_{4} \tag{10} \]

根据数据的时间关系，考虑到数据流的帧交错，为了保证同一帧的数据相加，就必须采取措施使“先头”数据潜伏一段时间，当同一帧的数据到达加法器输入端时，“先头”数据浮出执行加法操作。例如，把\(a_{1}\)视为“先头”数据，该数据直接通过加法器到其输出端，但不能立即反馈到加法器输入端，因为此时加法器输入端为\(a_{2}\)而非\(b_{1}\)，所以必须对其潜伏。当加法器输入端为\(b_{1}\)时，\(a_{1}\)在加法器反馈段浮出实现与\(b_{1}\)的相加。这种潜伏可通过级联的寄存器实现，也可通过FIFO实现。

图4. 滑动累加器硬件结构

滑动累加器的硬件结构如图4所示，图中采用了FIFO实现潜伏，FIFO深度为3（加法器输出已有一个时钟周期的寄存）。对于潜伏周期较长，速度要求较高的场合，采用FIFO更为合适；而对潜伏周期较短、速度要求不高的场合，采用级联的寄存器为宜或者采用移位寄存器SRL。图中，信号ce为使能相加，当其为高时允许加法器执行加法操作，否则din端数据直接输出。capture为捕获信号，当其为高时捕获节点P数据并输出给dout，否则保持不变。

与图4相对应的时序图如图5所示。图中\(s_{11}=a_{1}+b_{1},s_{21}=a_{2}+b_{2},s_{31}=a_{3}+b_{3},s_{41}=a_{4}+b_{4},s_{12}=a_{1}+b_{1}+c_{1},s_{22}=a_{2}+b_{2}+c_{2},s_{32}=a_{3}+b_{3}+c_{3},s_{42}=a_{4}+b_{4}+c_{4}\)。

图5. 滑动累加器时序图

滑动加法器设计的关键是确定FIFO（或级联寄存器）的深度以保证正确的潜伏周期，而此深度与帧的个数有关，例如，此设计中共有四帧数据，故FIFO深度为4-1=3。因为加法器输出有一级缓存。使能相加信号ce和捕获信号capture可根据图中时序设计。