1. IQ调制和解调
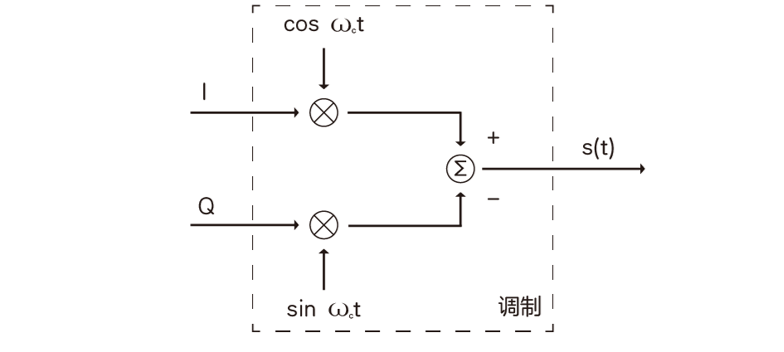
典型的IQ调制和解调如下图所示：
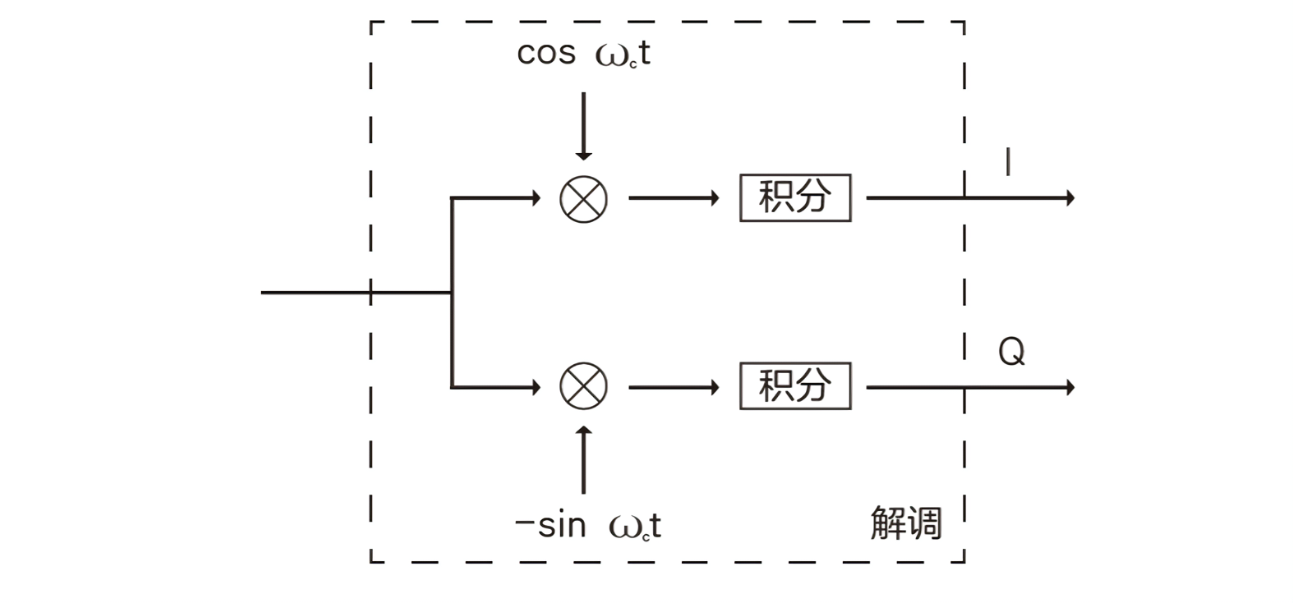
图1：IQ调制和解调示意图
考虑发送端待传输的信号为复数信号：
\[x(t) = x_{i}(t) + x_{q}(t) \tag{1}
\]
IQ调制器的输出信号为：
\[y(t)=R\{x(t)e^{j2\pi f_{c}t}\}=x_{i}cos(2\pi f_{c}t)-x_{q}sin(2\pi f_{c}t) \tag{2}
\]
如图所示，源信号\(x(t)\)的通向成分和正交成分分别调制到载波的同相成分和正交成分上进行发送。
在接收端，分别用\(\text{cos}(2\pi f_{c}t)\)和\(\text{sin}(2\pi f_{c}t)\)乘以\(\hat{y}(t)\)（接收端接收到的信号）即可恢复出原始的发送信息，其对应的数学表达式如下：
\[\begin{aligned}
\hat{x}_{i} &=\text{LPF}\{\hat{y}\text{cos}(2\pi f_{c}t) \} = \text{LPF}\{(x_{i}\text{cos}(2\pi f_{c}t)-x_{q}\text{sin}(2\pi f_{c}t))\times \text{cos}(2\pi f_{c}t) \} \\
&= \text{LPF}\{x_{i}\text{cos}(2\pi f_{c}t)\cdot \text{cos}(2\pi f_{c}t) -x_{q}\text{sin}(2\pi f_{c}t)\cdot \text{cos}(2\pi f_{c}t) \} \\
&=\text{LPF}\{\frac{1}{2}x_{i}(1+\text{cos}(4\pi f_{c}t))-\frac{1}{2}x_{q}\text{sin}(4\pi f_{c}t)\} \\
&= \frac{1}{2}x_{i}
\end{aligned}
\tag{3}
\]
其中常数1/2可以忽略，由此可以看出接收端完全恢复了源信号的同相分量。其中LPF{}表示低通滤波，能够将\(\text{cos}(4\pi f_{c}t)\)和\(\text{sin}(4\pi f_{c}t)\)所代表的高频分量滤除。
同理，可以得到源信号的正交分量\(x_{q}(t)\)恢复如下：
\[\begin{aligned}
\hat{x}_{q} &=\text{LPF}\{\hat{y}\text{sin}(2\pi f_{c}t) \} = \text{LPF}\{(x_{i}\text{cos}(2\pi f_{c}t)-x_{q}\text{sin}(2\pi f_{c}t))\times \text{sin}(2\pi f_{c}t) \} \\
&= \text{LPF}\{x_{i}\text{cos}(2\pi f_{c}t)\cdot \text{sin}(2\pi f_{c}t) -x_{q}\text{sin}(2\pi f_{c}t)\cdot \text{sin}(2\pi f_{c}t) \} \\
&=\text{LPF}\{\frac{1}{2}x_{i}(\text{sin}(4\pi f_{c}t))-\frac{1}{2}x_{q}(1-\text{cos}(4\pi f_{c}t))\} \\
&= \frac{1}{2}x_{q}
\end{aligned}
\tag{4}
\]
其中的常数\(-1/2\)可以忽略，接收机会进行相应的幅度和相位补偿。
2. IQ失配表征(IQ imbalance = IQ mismatch)
正交调制和解调通常是以模拟电路的方式实现，但是模拟电路中正交调制和解调所需要的IQ两路混频载波信号很难做到像数字信号那样精确匹配（幅度相等，相位正好相差90度）。这种幅度和相位的不匹配统称为IQ失配，也可以区分开来分别叫做幅度失配和相位失配。
考虑IQ失配后，把载波信号表示如下：
\[c(t)=\text{cos}(f_{c}t)+j(1+a)\text{sin}(2\pi f_{c}t + \phi) \tag{5}
\]
其中\(a,\phi\)分别表示载波信号的正交分量相对于同相分量的幅度和相位偏差。这样就可以考虑IQ失配后的正交调制输出信号为：
\[y(t)=R\{x(t)\cdot c(t)\}=x_{i}(t)\text{cos}(2\pi f_{c}t)-x_{q}(t)(1+a)\text{sin}(2\pi f_{c}t) \tag{6}
\]
3. IQ失配的影响
3.1 镜像分量
首先，IQ失配会在发射信号频谱中产生镜像分量。下图所示为载波为2.5MHz，单频信号1MHz，无IQ失配和有IQ失配(\(\phi=5^{。},a=0.25\))条件下的正交调制输出的频谱对比。如图中所示，存在IQ失配时，在1.5MHz有一个镜像分量。
在双边带通信中，这个镜像分量出现有效信道带宽内并被有效信号掩盖，不会对邻道产生影响。但是在单边带通信中，镜像分量出现在邻信道会对邻道通信产生影响。因此，必须对其进行一定的抑制。
3.2 解调性能下降
在接收端按照理想的方式对以上存在IQ失配的正交调制输出信号进行正交解调可以得到：
\[\begin{aligned}
\hat{x}_{i} &= LPF\{\hat{y}cos(2\pi f_{c}t) \} \\
&= LPF\{(x_{i}cos(2\pi f_{c}t)-x_{q}(t)(1+a)sin(2\pi f_{c}t+\phi))\times cos(2\pi f_{c}t) \} \\
&= \frac{1}{2}[x_{i}-x_{q}(1+a)sin(2\pi f_{c}t)]
\end{aligned}
\tag{7}
\]
\[\begin{aligned}
\hat{x}_{q} &=\text{LPF}\{\hat{y}\cdot \text{sin}(2\pi f_{c}t) \} = \frac{1}{2}[x_{1}(1+a)\text{cos}(\phi)]
\end{aligned}
\tag{8}
\]
由上式可以看出，正交解调的输出信号不再忠实地反映发射端的源信号，而是有一定程度的失真。尤其是同相分量受到了来自正交分量信号的串扰。这必然会导致接收性能的下降。
