连续相位调制(CPM)

1. CPFSK调制原理

先回顾FSK的调制的时域表达式为：

\[\begin{aligned} s_{m}(t)&=\sqrt{\frac{2\mathcal{E}}{T}}\text{Re}\left[e^{j(m\Delta f)t}e^{j2\pi f_{c}t}\right]\\ s_{ml}(t) &= \sqrt{\frac{2\mathcal{E}}{T}}e^{j(m\Delta f)t} \end{aligned} \tag{1.1}\]

其中频移量\(\color{red}{m\Delta f，m=1,2,\cdots,M}\)映射所要发送的数字信息。FSK调制的实现方法为：使用\(M=2^{k}\)个调谐到期望频率的振荡器，根据时间间隔T内要发送的特定的k个比特，从M个频率中选择一个频率。然而这么做会导致一个频率到另一个频率的突发切换，工程上突变建模为\(\delta(\cdot)\)函数，由此可知FSK波形的相位是不连续的，这将导致调制信号频谱的旁瓣过大，导致频谱利用率降低。

为了改善这一现象，提出了连续相位频移键控(Continuous Phase Frequency Shift Keying, CPFSK)。
为了表示CPFSK信号，以PAM信号：

\[d(t)=\sum_{n}I_{n}g(t-nT) \tag{1.2} \]

开始，式中\(I_{n}\)表示幅度序列，它是由信息序列\({a_{n}}\)来的\(k\)比特二进制数字组映射到幅度电平\(I_{n} = \pm 1, \pm 3, \cdots, \pm(M-1)\)得到的。而\(g(t)\)是一个幅度为 \(1/2T\) 且持续时间为\(T\)秒的矩形脉冲(面积为1/2)。信号\(d(t)\)用来对载波进行频率调制，从而等效低通波形可以表示为：

\[v(t) = \sqrt{\frac{2\mathcal{E}}{T}}e^{j[4\pi Tf_{d}\int_{-\infty}^{t}d(\tau)d\tau]+\phi_{0}} \tag{1.3} \]

其中，\(f_{d}\)是峰值频率偏移(Peak Frequency Deviation)，\(\phi_{0}\)表示载波的初始相位。相应的载波调制信号可以表示为：

\[\begin{aligned} s(t) &= \sqrt{\frac{2\mathcal{E}}{T}}\text{Re}[e^{j[4\pi Tf_{d}\int_{-\infty}^{t}d(\tau)d\tau]+\phi_{0}}e^{j2\pi f_{c}t}]\\ &=\sqrt{\frac{2\mathcal{E}}{T}}\cos[2\pi f_{c}t+\phi(t;I)+\phi_{0}] \end{aligned} \tag{1.4} \]

式中，\(\phi(t;I)\)表示载波的时变相位，为

\[\phi(t;I)=4\pi f_{d}T\int_{-\infty}^{t}d(\tau)d\tau=4\pi f_{d}T\int_{-\infty}^{t}[\sum_{n}I_{n}g(\tau-nT)]d\tau \tag{1.5} \]

式中，\(d(t)\)信号是不连续的，但是其积分是连续的(注，式中的"\(4\)"单纯是为了后续的计算方便添加的，因为可以把矩形脉冲幅度里面的1/2抵消掉，然后恰好可以把"\(4\pi\)"变成"\(2\pi\)"，使之能够满足角频率与频率的转换关系)。所以载波的相位变化是连续的，调制后载波信号的相位在时间区间\([nT,(n+1)T]\) 可以表示为：

\[\begin{aligned} \phi(t;I)&=4\pi f_{d}T\sum_{k=-\infty}^{n-1}\int_{kT}^{(k+1)T}I_{k} g(t-kT)dt+4\pi f_{d}T\int_{nT}^{t}I_{n} g(\tau-nT)d\tau\\ &=4\pi f_{d}T\sum_{k=-\infty}^{n-1}I_{k} \int_{kT}^{(k+1)T}\frac{1}{2T}dt+4\pi f_{d}T I_{n}\int_{0}^{t} g(\tau)d\tau, \quad t\in[0,T]\\ &=2\pi f_{d}T\sum_{k=-\infty}^{n-1}I_{k}+2\pi\cdot 2f_{d}T\cdot I_{n}\cdot \int_{0}^{t}g(\tau)d\tau\\ &=\theta_{n}+2\pi h I_{n}q(t-nT) \end{aligned} \tag{1.6} \]

式中，\(h\)表示调制指数，调制指数越大，调制后的两个载波频率差值越大；\(\theta_{n}\)是时间区间\([0,(n-1)T]\)内的累积相位，\(q(t)\)为相位响应函数，是频率成形滤波器\(g_{T}(t)\)的积分，它们可以表示为：

\[h=2f_{d}T \tag{1.7} \]

\[\theta_{n} = \pi h \sum_{k=-\infty}^{n-1} I_{k} \tag{1.8} \]

\[q(t) = \left \{\begin{aligned} &0, t \le 0 \\ &t/2T, 0<t<T \\ &1/2, t>T \end{aligned} \right. \tag{1.9} \]

CPFSK调制是用将要发送的基带数据控制一个单一频率的载波，载波的相位变化是连续的，有效地抑制了频谱旁瓣，调制后信号的带宽变窄。

2. 连续相位调制

CPFSK实际上是一般类型连续相位调制（CPM）信号的一个特例，CPM的载波相位是：

\[\phi(t;I)=2\pi\sum_{k=-\infty}^{n}I_{k}h_{k}q(t-kT),\quad nT\le t \le (n+1)T\tag{2.1} \]

式中，\(\{I_{k}\}\)是由符号表\(\pm1, \pm3, \cdots,\pm (M-1)\)中选出的M元信息符号序列，\(\{h_{k}\}\)表示调制指数序列，而\(q(t)\)是某个归一化波形。当对所有k有\(h_{k}=h\)时，调制指数对所有的符号都是固定的。当调制指数随着某一个符号到另一个符号而变化时，该信号称为多重 h CPM。在这种情况下，\(\{h_{k}\}\)以循环方式在调制指数集中变化。波形q(t)一般可以表示成某个脉冲\(g(t)\)的积分，即

\[q(t)=\int_{0}^{t}g(\tau)d\tau \tag{2.2} \]

如果对t>T有\(g(t)=0\)，则CPM信号称为全响应CPM。如果t>T有\(g(t)\ne 0\)，则已调信号称为部分响应CPM。

图2.1说明了g(t)的几种脉冲形状及其相应的q(t)。易见，通过选择不同的脉冲形状g(t)以及改变调制指数和符号数目M，就可以产生无穷多种CPM信号。注意，CPM信号的记忆性，是通过相位的连续性引入的。

图2.1 CPM的脉冲形状：全响应CPM(a,b)，部分响应(c,d)和GMSK(e)

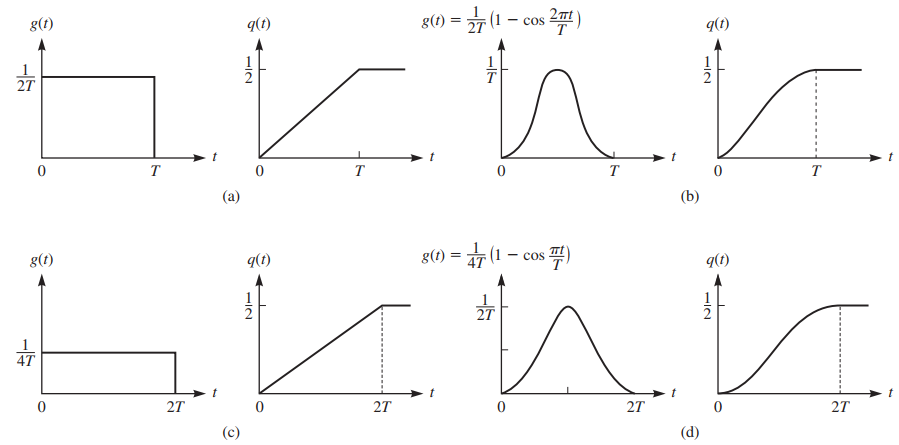
表2.1列出了三种常用的CPM脉冲形状。LREC表示持续时间为\(LT\)的矩形脉冲，这里\(L\)为整数，图2.1(a)所示为\(L=1\)的CPFSK脉冲。图2.1(c)所示为\(L=2\)的LREC脉冲，LRC表示持续时间为\(LT\)的升余弦脉冲，图2.1(b),(d)分别为\(L=1,L=2\)的LRC脉冲。

表2.1 某些常用的CPM脉冲形状

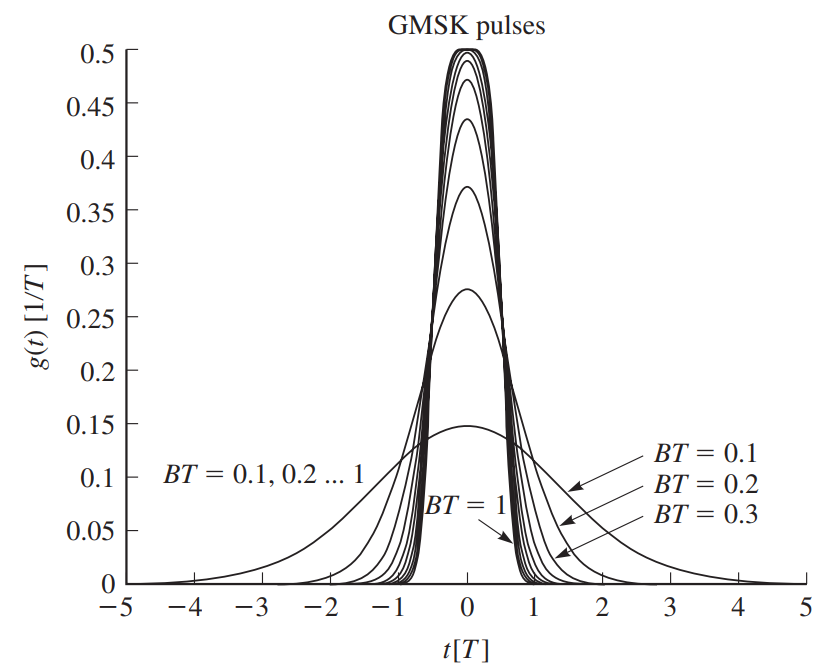
$$ \begin{array}{c|c} \hline \text{LREC} & g(t)=\left\{\begin{aligned}&\frac{1}{2LT},\quad &0\le t \le LT \\ &0, \quad &\text{otherwise} \end{aligned} \right.\\ \hline \text{LRC} & g(t)=\left\{\begin{aligned}&\frac{1}{2LT}(1-\text{cos}\frac{2\pi t}{LT}),\quad &0\le t \le LT \\ &0, \quad &\text{otherwise} \end{aligned} \right.\\ \hline \text{GMSK} & g(t)=\frac{Q(2\pi B(t-\frac{T}{2}))-Q(2\pi B(t+\frac{T}{2}))}{\sqrt{ln2}}\\ \hline \end{array} $$

表2.1中的第3种脉冲称为具有带宽参数\(B\)的高斯最小移频键控(Gaussian Minimum-Shift Keying, GMSK)脉冲，B表示高斯脉冲的\(-3dB\)带宽。图2.2所示为时间-带宽乘积BT范围为0.1~1的一组GMSK脉冲。

图2.2 GMSK脉冲形状

3. 最小移频键控(MSK)

MSK是二进制CPFSK的一个特例，其调制指数\(h=1/2\)，将其带入式(1.6)，可以得到在\(nT\le t \le (n+1)T\)间隔中的载波相位是

\[\begin{aligned} \phi(t;I) &=\pi h \sum_{k=-\infty}^{n-1}I_{k}+2\pi h \cdot I_{n}\cdot \int_{0}^{t}g(\tau)d\tau\\ &=\frac{1}{2}\sum_{k=-\infty}^{n-1}I_{k}+\pi I_{n}\cdot \frac{t-0}{2T},\quad t\in [0,T]\\ &=\theta_{n}+\frac{1}{2}\pi I_{n}\frac{t}{T} \end{aligned} \tag{3.1} \]

带入式(1.4)可以得到相应的已调载波信号为

\[\begin{aligned} s(t) &= \sqrt{\frac{2\mathcal{E}}{T}}\cos[2\pi f_{c}t+\phi(t;I)+\phi_{0}]\\ &= \sqrt{\frac{2\mathcal{E}}{T}}\cos[2\pi f_{c}t+\theta_{n}+\frac{1}{2}\pi I_{n}\frac{t}{T}+\phi_{0}]\\ &= \sqrt{\frac{2\mathcal{E}}{T}}\cos\left[2\pi \left(f_{c}+\frac{1}{4T}I_{n}\right)t+\theta_{n}+\phi_{0}\right]\\ \end{aligned} \tag{3.2} \]

上式表明：二进制CPFSK信号可以表示成在\(nT\le t \le (n+1)T\)间隔中具有两个频率之一的正弦波。定义这两个频率分别为

\[f_{1} = f_{c}-\frac{1}{4T},\quad f_{2} = f_{c}+\frac{1}{4T}\tag{3.3} \]

那么式(3.2)可写为

\[s_{i}(t)=\sqrt{\frac{2\mathcal{E}}{T}}\cos(2\pi f_{i}t+\theta_{n}+\phi_{0}),\quad i=1,2\tag{3.4} \]

可以看到 \(s_{1}(t),s_{2}(t)\) 的频率间隔为\(\Delta f=f_{2}-f_{1}=\frac{1}{2T}\)。这是确保在长度为T的信号传输间隔上信号\(s_{1}(t),s_{2}(t)\)正交的最小频率间隔。这就解释了为什么具有\(h=1/2\)的二进制CPFSK称为最小频移键控(MSK)。

3. GFSK的MATLAB代码实现

首先实现“经过高斯滤波的矩形脉冲”，也即是式\((2.5)\)中的\(g(t)\)。

function [Gaussian_filter_q] = Gaussian_filter(B, symb_rate, delay, ts)
% INPUTS:
%   B         : the 3dB bandwidth of Gaussian filter
%   symb_rate : rate of the symbol, in ble it is 1e6 symbol/s
%   delay     : it controls how many symbols the Gaussian filter cover
%   ts        : the reciprocal of sample rate
  symb_T  = 1 / symb_rate;
  Gau_t   = -delay*symb_T:ts:delay*symb_T;
  K       = 2*pi*B / sqrt(log(2));
  Gau_det = K.*(Gau_t - symb_T / 2);
  Gau_sum = K.*(Gau_t + symb_T / 2);
  Gaussian_filter_q = 1/(2*symb_T)*[qfunc(Gau_det)-qfunc(Gau_sum)];
end

然后设定参数进行测试：

clear
clc

h = 0.5 ; % the modulation index h = 2f_{d}T
sample_rate = 26e6; % the sample rate
sample_time = 1/sample_rate;
symbol_rate = 1e6;
oversample = sample_rate / symbol_rate;
B = 0.5e6; % the 3db bandwidth is 500Mhz
delay = 1.5 % the gaussian filter covers 3 symbol
tx_bits = [1,0,0,1,0,0,1,0,1,1,1,0,1,1,0,0,1]; % the transmit bits

Gaussian_filter_coeff = Gaussian_filter(B, symbol_rate, delay, sample_time);
tx_data = 2*tx_bits - 1; % NRZ code
tx_data_sample = upsample(tx_data, oversample);
tx_data_filtered = 2*pi*h*conv(Gaussian_filter_coeff,tx_data_sample);

tx_phase = sample_time*cumsum(tx_data_filterd);
tx_cos = cos(tx_phase);
tx_sin = sin(tx_phase);

tx_gfsk = complex(tx_cos,tx_sin);

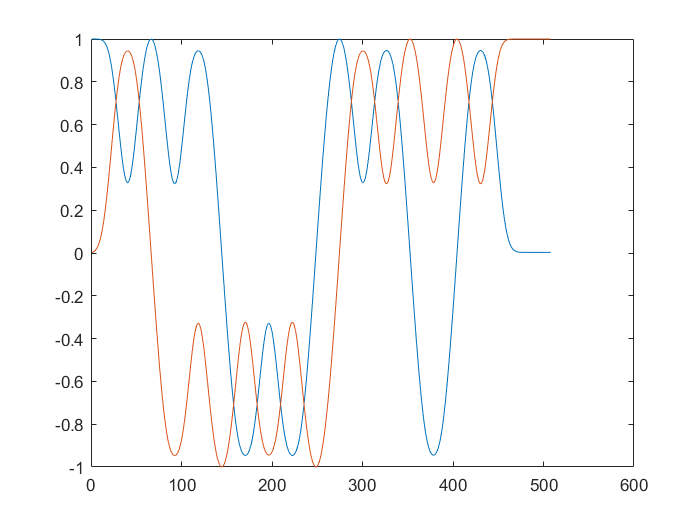
plot(tx_cos); 
hold on 
plot(tx_sin);
hold off

最终波形如下：

The gfsk wave.