【刷题-PAT】A1135 Is It A Red-Black Tree （30 分）

1135 Is It A Red-Black Tree （30 分）
There is a kind of balanced binary search tree named red-black tree in the data structure. It has the following 5 properties:
(1) Every node is either red or black.
(2) The root is black.
(3) Every leaf (NULL) is black.
(4) If a node is red, then both its children are black.
(5) For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.
For example, the tree in Figure 1 is a red-black tree, while the ones in Figure 2 and 3 are not.

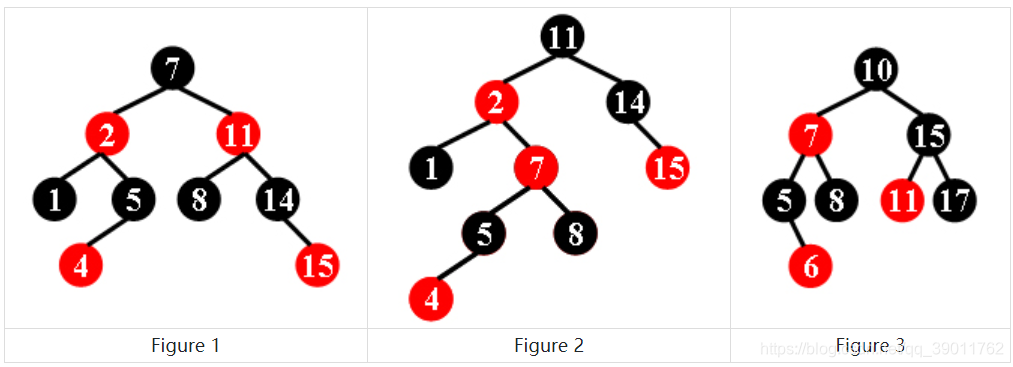
For each given binary search tree, you are supposed to tell if it is a legal red-black tree.
Input Specification:
Each input file contains several test cases. The first line gives a positive integer K (≤30) which is the total number of cases. For each case, the first line gives a positive integer N (≤30), the total number of nodes in the binary tree. The second line gives the preorder traversal sequence of the tree. While all the keys in a tree are positive integers, we use negative signs to represent red nodes. All the numbers in a line are separated by a space. The sample input cases correspond to the trees shown in Figure 1, 2 and 3.
Output Specification:
For each test case, print in a line "Yes" if the given tree is a red-black tree, or "No" if not.
Sample Input:
3
9
7 -2 1 5 -4 -11 8 14 -15
9
11 -2 1 -7 5 -4 8 14 -15
8
10 -7 5 -6 8 15 -11 17
Sample Output:
Yes
No
No
分析：红黑树需要满足三个条件：
1. 根节点是黑色的
2. 红色节点的孩子节点是黑色的
3. 任何节点左右子树的黑色节点个数相等（由路径中的黑色节点个数相等推出）
条件1直接判断，条件2和3递归实现，具体的思路来自于AVL树的求高度等一系列操作

#include<iostream>
#include<cstdio>
#include<vector>
#include<unordered_map>
#include<string>
#include<set>
#include<algorithm>
#include<cmath>
using namespace std;
const int nmax = 50;
int pre[nmax] = {0};
struct node{
    int data;
    node *lchild, *rchild;
};
typedef node* pnode;
pnode creat(int pL, int pR){
    if(pL > pR)return NULL;
    pnode root = new node;
    root-> data = pre[pL];
    root->lchild = root->rchild = NULL;
    int pos = pL + 1;
    while(pos <= pR && abs(pre[pos]) < abs(pre[pL]))pos++;
    root->lchild = creat(pL + 1, pos - 1);
    root->rchild = creat(pos, pR);
    return root;
}
bool judge1(pnode root){
    if(root == NULL)return true;
    if(root->data < 0){
        if(root->lchild != NULL && root->lchild->data < 0)return false;
        if(root->rchild != NULL && root->rchild->data < 0)return false;
    }
    return judge1(root->lchild) && judge1(root->rchild);
}
int getH(pnode root){
    if(root == NULL)return 0;
    int l = getH(root->lchild), r = getH(root->rchild);
    return root->data > 0 ? max(l, r) + 1 : max(l, r);
}
bool judge2(pnode root){
    if(root == NULL)return true;
    int l = getH(root->lchild), r = getH(root->rchild);
    if(l != r)return false;
    return judge2(root->lchild) && judge2(root->rchild);
}
int main(){
    #ifdef ONLINE_JUDGE
    #else
    freopen("input.txt", "r", stdin);
    #endif
    int n;
    scanf("%d", &n);
    for(int i = 0; i < n; ++i){
        int m;
        scanf("%d", &m);
        for(int j = 0; j < m; ++j)scanf("%d", &pre[j]);
        pnode root = creat(0, m - 1);
        if(root->data < 0 || judge1(root) == false || judge2(root) == false)printf("No\n");
        else printf("Yes\n");
    }
    return 0;
}