2019美赛B题

问题B：发送无人机：开发空中灾难救援响应系统

背景：2017年，遭受美国波多黎各领土袭击的最严重飓风（见附件1）使该岛遭受严重破坏，造成2900多人死亡飓风风暴潮和波浪作用的综合破坏力对建筑物，房屋和道路造成了广泛的破坏，尤其是波多黎各东部和东南沿海地区。风暴和暴雨带来的风暴击倒了波多黎各80％的电线杆和所有输电线路，导致岛上340万居民基本丧失了电力。此外，风暴还破坏或摧毁了岛上大部分的蜂窝通信网络。岛上大部分地区的电力和电池服务中断持续数月，而在某些地区则更长。广泛的洪水阻塞并破坏了岛上的许多高速公路和道路，使得紧急服务地面车辆几乎不可能规划和导航他们的路线波多黎各的全面破坏程度在一段时间内仍不明朗;数十个地区被孤立，没有沟通对医疗用品，救生设备和治疗紧张的保健诊所，医院急诊室和非政府组织（NG）救济行动的需求。由长期病患转向医院和临时住所接受护理，医疗保健需求持续激增一段时间。

问题：非政府组织（NGO）经常面临在自然灾害期间或之后提供充分和及时响应的挑战，例如2017年袭击美国波多黎各领域的飓风。特别是一个非政府组织-HELP，Inc。-该公司正试图通过设计一种名为“DroneGo”的可移动灾难响应系统来提高其响应能力.Dronone将使用旋翼无人机提供预先封装的医疗用品并提供高分辨率航拍视频侦察。选定的无人机应该HELP，Inc。已经确定了各种候选转子翼无人机，希望您的团队考虑将其用于设计其DroneGo车队（见附件2,3）。

DroneGo的预包装医疗用品，称为医疗包，旨在增加而不是取代受灾害影响的国家内现场医疗援助组织提供的用品.HELP，Inc。计划推出三种不同的医疗包，称为MED1，MED2和MED3。无人机将在无人机货舱内携带这些医疗包裹，以便运送到选定的地点（见附件4,5）。根据用于运输医疗用品的特定无人机，可能可以在单个无人机货舱中运输多个医疗包。请注意，无人机必须降落在地面上以从无人机货舱卸载医疗用品。无人机的视频功能将为HELP，INC的地面路线规划指挥和控制中心提供损坏和可维修的交通道路网络的高分辨率视频。

HELP，Inc。将使用国际标准组织（ISO）标准干货集装箱快速将完整的DroneGo灾难响应系统运输到特定的灾区.DroneGo车队中所有无人机的各个集装箱，以及所有必需的医疗包装必须最多容纳三个ISO货物集装箱才能运送到一个地方，如果在灾区使用三个货物集装箱，则最多可容纳三个不同的位置。应包装每个运输容器的内容，以便最大限度地减少对未使用空间的缓冲材料的需求。表1显示了ISO标准干货集装箱的尺寸

 

题目解析

本题属于典型的规划类问题，目的是为了让发生飓风等自然灾害时，可以利用无人机更加高效地进行物资上的运输。

问题一

考虑的是无人机、医疗包、ISO 集装箱之间的关系，目的是为了满足附件四中各地对于医疗包的需求。那么既然是规划类问题，那么我们必须要明确目标方程根据题意目标方程应该是：

·         运输医疗包的总量和种类大于等于各个医院的需求。

·         为了成本考虑，尽量使无人机数量少

·         每个无人机舰队中必须有带有视频功能的无人机等

 

限定条件：

·         各个无人机运输的能力，包括大小与重量。

·         医疗包需要放在无人机运输包装内，再放入无人机运输舱内，所以要考虑这三者之间的大小限制关系。

·         集装箱的存放能力

 

解决方法：根据自己的理解建立合适的目标方程以及限定条件编程能力比较好的对，可以直接使用软件解决，编程能力不好的队，则需要考虑多目标变单目标，再进行考虑。

 

问题二

在第一问的基础上，再加入地理因素，即考虑医疗包的及时送达问题。这依旧属于规划问题，我们需要考虑的是在波多黎各州哪一个位置安装这三个集装箱才是最快速或者说最均衡的，让医疗包送达指定医院。

目标方程：

·         集装箱安装点与各地距离的总和最小。

·         运输医疗包的时间综合最小

·         需要无人机的数量最小等

限定条件：

·         与问题一相同。

·         无人机的飞行时间与飞行速度限制，这是一个较为麻烦的问题，

 

因为各限制因素间的制约会随着方案的改变而产生影响，这可以理解成为一个动态规划的问题，同时需要注意的是，题目中并没有明确要求集装箱的安装方案，所以集装箱不一定安装在同一个位置，所以具体情况需要依据目标方程以限定条件来确定。模型的关键点在于建立一个自己可以解出的方程组，需要根据自己对题意的理解以及实际能力来决定，言之有理即可。

 

算法

1、 建立基于BP神经网络的蚁群算法模型，然后使用matlab对其进行模拟驯良，从局部最优值跳到理论上的全局最优值。最终通过matlab 进行模拟，得出最优模型。

2、 检验车队的的正确性和最优性。此时我们应该不能只考虑单维度的元素，应该关注多维度的影响和冲击。最后在第一问的基础上建立无人机货舱中运输医疗包基于禁忌算法TSP 的自适应算法模型。

 

蚁群算法

算法提出

核心思想：

1、 选择机制：迹越多的路径，被选中的概率越大；

2、 迹更新机制：路径越短，迹增加越快；

3、 协作机制：个体之间通过迹进行信息交流。

 

算法流程

（一）蚁群优化算法实现（以TSP问题为例）：

1、 初始化，将m只蚂蚁放入到n个随机选择的城市中。

2、 选择机制：每一只蚂蚁每一步的行动是，根据一定的依据选择下一个它还没有访问的城市；

3、 迹更新机制：在完成一步（从一个城市到达另外一个城市）或者一个循环（完成对所有n个城市的访问）后，更新所有路径上的残留信息浓度。

4、 判断是否停止算法，停止则输出最优结果；否则，返回第二步。

（二）选择机制，选择下一个城市的依据主要是两点：

1、 t 时刻连接城市 i 和 j 的路径上残留信息（迹）的浓度  

2、 由城市 i 转移到城市 j 的启发信息，该启发信息是由要解决的问题给出的，在TSP问题中一般取，其中，表示城市 i，j 间的距离，在这里可以称为先验知识。

3.、 选择机制

那么，t 时刻位于城市 i 的蚂蚁 k 选择城市 j 为目标城市的概率是：

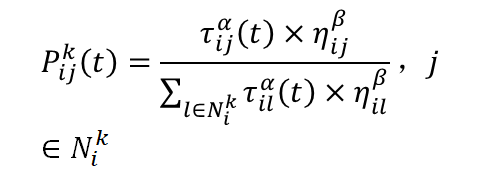
：残留信息的相对重要程度；

：启发信息的相对重要程度；

：所有可能的目标城市，即还没有访问的城市。为了避免对同一个城市的多次访问，每一只蚂蚁都保存一个列表tabu(k)，用于记录到目前为止已经访问的城市；

：t时刻蚂蚁由 i 城市到 j 城市的概率。

 

4、 迹更新机制

为了避免残留信息过多引起的残留信息淹没启发信息的问题，在每一只蚂蚁完成对所有n个城市的访问后（也即一个循环结束后）或每走一步（从一个城市到下一个城市后），必须对残留信息进行更新处理， Morigo介绍三种迹更新机制：

ant-cycle算法

在每一只蚂蚁完成对所有n个城市的访问后，对旧的信息进行削弱，将最新的蚂蚁访问路径的信息加入。 

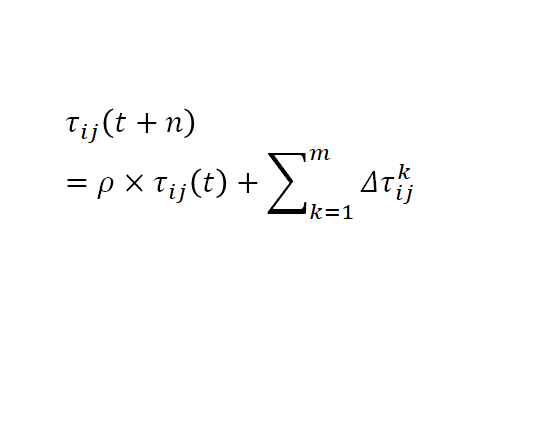
：残留信息的保留部分；

：残留信息被削弱的部分，小于1；

  ：蚂蚁k在时间段t到t+n内的访问过程中，在i到j的路径上留下的残留信息浓度；

Q  ：为常量；

Lk  ：蚂蚁k在本次循环中所选择路径的总长度。

 

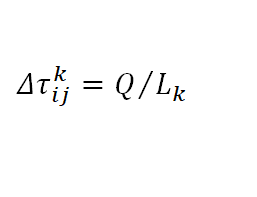
：蚂蚁k在时间段t到t+n内的访问过程中，在i到j的路径上留下的残留信息浓度；

Q  ：为常量；

Lk  ：蚂蚁k在本次循环中所选择路径的总长度；如果没有选择i到j的路径，则

 

ant-density算法

在每一只蚂蚁完成下一个个城市的访问后，对旧的信息进行削弱，将最新的蚂蚁访问路径的信息加入

 

：蚂蚁k选择i到j的路径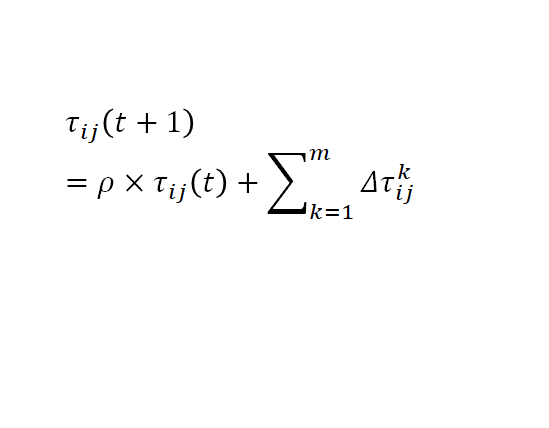

：蚂蚁k选择i到j的路径

：蚂蚁k没有选择i到j的路径

 

ant-quantity算法

在每一只蚂蚁完成下一个个城市的访问后，对旧的信息进行削弱，将最新的蚂蚁访问路径的信息加

入     

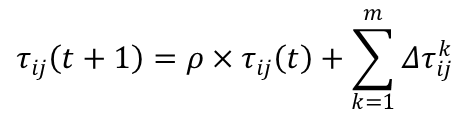
：蚂蚁k选择i到j的路径

：蚂蚁k没有选择i到j的路径

 

三种算法的比较

ant-cycle算法的效果最好，这是因为它用的是全局信息——Q/Lk；

ant-density、ant-quantity算法用的是局部信息——Q、Q/dij。

 

（三）改进/优化

1）MAX-MIN ANT SYSTEM （MMAS）算法

A． 只对最佳路径增加迹的浓度，从而更好地利用了历史信息；

B．为了避免算法过早收敛于并非全局最优的解，将各条路径可能的迹浓度限制于，超出这个范围的值被强制设为或者为，可以有效地避免某条路径上的信息量远大于其余路径，使得所有的蚂蚁都集中到同一条路径上；

C.    将各条路径上迹的初始浓度设为，这样便可以更加充分地进行寻优。

2）自适应蚁群优化算法

问题：蚁群算法的主要依据是信息正反馈原理和某种启发式算法的有机结合。在构造解的过程中，利用随机选择策略，这种选择策略使得进化速度慢；正反馈原理旨在强化性能较好的解，却容易出现停滞现象。

解决：从选择策略方面进行修改，采用确定性选择和随机选择相结合的选择策略，并在搜索过程中动态地调整确定性选择的概率。进化到一定代数后，进化方向已经基本确定，这时对路径上信息量作动态调整，缩小最好和最差路径上的信息两的差距，并适当增大随机选择的概率，以利于对解空间的更完全搜索。

 

3）自适应调整信息素的蚁群算法

该算法由下式确定蚂蚁 k 从 i 城市转移到 s 城市

 

 

 

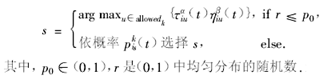
问题：蚁群算法的主要依据是信息正反馈原理和某种启发式算法的有机结合。在构造解的过程中，利用随机选择策略，这种选择策略使得进化速度慢；正反馈原理旨在强化性能较好的解，却容易出现停滞现象。

解决：根据搜索进展情况，动态修改需要增加的信息素的方法。算法采用时变函数Q（t）来替代调整信息素中常量Q，即 ， Q（t）随着人工蚂蚁搜索过程做实时的调整和变化

自适应调整策略：通过对算法的监控，实时判断算法的搜索状态，如果一段时间内获得的最优解没有变化，则减少要添加的信息素，即减少中的Q（t）。

 

 

 

 

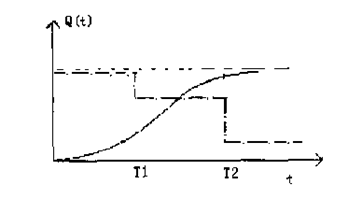
Q（t）时变函数几个例子，针对不同情况使用

 

4）自适应调整（残留信息的保留部分）的蚁群算法

问题：当问题规模比较大时，由于信息素的挥发系数 1- 的存在，使那些从未被搜索到的解上信息素会减少到接近于0，降低了算法的全局搜索能力，而且过大时，以前搜索过册解被选择的可能性过大，也会影响到算法全局搜索能力；通过减少，虽然可以提高算法的全局搜索能力，但又会使算法的收敛速度降低。

解决：自适应调整的值，的初始值为=1；当算法求得的最优值在N次循环内没有明显改进时，减为：

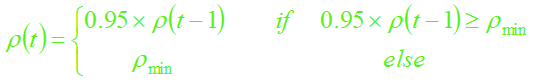
5）带杂交算子的蚁群算法

6）在解决TSP问题——分段算法Section_MMMAS

7）在解决TSP问题——相遇算法MMMAS

 

（四）连续问题

最初的蚁群算法思想起源于离散型的网络路径问题，因此，在一般函数优化问题中，必须对许多实施细节加以修正。

第一，转移概率

第二，强度更新方程

 

寻优过程：

一般函数优化的蚁群优化算法流程：