【数字图像处理】 图像平滑

图像平滑从信号处理的角度看就是去除其中的高频信息，保留低频信息。因此我们可以对图像实施低通滤波。低通滤波可以去除图像中的噪音，模糊图像(噪音是图像中变化比较大的区域，也就是高频信息)。而高通滤波能够提取图像的边缘(边缘也是高频信息集中的区域)。

根据滤波器的不同又可以分为均值滤波，高斯加权滤波，中值滤波， 双边滤波。

均值滤波

平均滤波是将一个m*n(m, n为奇数)大小的kernel放在图像上，中间像素的值用kernel覆盖区域的像素平均值替代。平均滤波对高斯噪声的表现比较好，对椒盐噪声的表现比较差。

$$ g(x,y) = \frac{1}{mn}\sum_{(x,y) \in S_{xy}} f(s,t)$$

其中$S_{xy} 表示中心点在(x, y) 大小为m X n 滤波器窗口。

当滤波器模板的所有系数都相等时，也称为盒状滤波器。BoxFilter ， BoxFilter可以用来计算图像像素邻域的和。

cv2.boxFilter() normalize=False， 此时不使用归一化卷积窗，当前计算像素值为邻域像素和。

加权均值滤波器不同于上面均值滤波器的所有像素系数都是相同的，加权的均值滤波器使用的模板系数，会根据像素和窗口中心的像素距离取不同的系数。比如距离中心像素的距离越近，系数越大。

$$\frac{1}{16}

\left [

\begin{array}{ccc}

1 & 2 & 1 \\ 2 & 4 & 2 \\ 1 & 2 & 1

\end{array}

\right ]

$$

一般的作用于M*N大小的图像，窗口大小为m*n的加权平均滤波器计算公式为：

$$g(x, y) = \frac{\sum_{s = -a}^a \sum_{t = -b}^b w(s, t) f(x+s, y+t)}{\sum_{s = -a}^a \sum_{t = -b}^b w(s, t)}$$

 

高斯加权滤波器

高斯函数是一种正态分布函数，一个二维高斯函数如下：

$$hh(x, y) = \frac{1}{2\pi \sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}$$

$\sigma$为标准差， 如果要得到一个高斯滤波器模板可以对高斯函数进行离散化，得到离散值作为模板系数。简单来说就是以模板中心位置为坐标原点进行取样。

高斯加权平均中，最重要是$\sigma$的选取，标准差代表数据离散程度，如果$\sigma$小那么，高斯分布中心区域更加聚集，平滑效果越差；反之，则更离散，平滑效果越明显。

中值滤波

前面提到的都是线性平滑滤波器(中间像素值是由邻域像素值线性加权得到)，而中值滤波器，使用滤波器窗口包含区域的像素值的中值来得到窗口中心的像素值，本质上是一种非线性平滑滤波器。中值滤波器对于去除impulse noise或者salt-and-pepper noise非常有效， 对于gaussian noise的表现则比较差。

import cv2
import numpy as np 
from skimage.util import random_noise
from matplotlib import pyplot as plt
import skimage.io
from skimage import img_as_ubyte
"""
Created on 2018.07.02
@author: vincent


"""


def salt(img, n):
	for k in range(n):
		i = int(np.random.random()*img.shape[1])
		j = int(np.random.random()*img.shape[0])
		if img.ndim==2:
			img[j.i] = 0;
		elif img.ndim==3:
			img[j,i,0] = 255
			img[j,i,1] = 255
			img[j,i,2] = 255


def pepper(img, n):
	for k in range(n):
		i = int(np.random.random()*img.shape[1])
		j = int(np.random.random()*img.shape[0])
		if img.ndim==2:
			img[j.i] = 0;
		elif img.ndim==3:
			img[j,i,0] = 0
			img[j,i,1] = 0
			img[j,i,2] = 0



if __name__ == "__main__":

	img = skimage.io.imread('/home/vincent/Pictures/work/lena.png')
	
	sigma = 0.1
	gaussian_img = random_noise(img, var = sigma**2)

	salt_img = random_noise(img, mode = 'salt')

	pepper_img = random_noise(img, mode = 'pepper')

	salt_pepper_img = random_noise(img, mode = 's&p')

	poisson_img = random_noise(img, mode='poisson')

	images = [img, gaussian_img, salt_img, pepper_img, salt_pepper_img, poisson_img]
	titles = ['origin', 'gaussian_noise', 'salt_noise', 'pepper_noise', 'salt_pepper_noise', 'poisson_noise']
	for i in range(6):
		plt.subplot(2,3, i+1)
		plt.title(titles[i])
		plt.imshow(images[i])
	

	# denoise on gaussian noise 
	plt.figure()
	#gaussian_img = cv2.cvtColor(gaussian_img.astype(np.uint8), cv2.COLOR_RGB2BGR)
	#gaussian_img = gaussian_img[:,:,::-1]

	gaussian_img = img_as_ubyte(gaussian_img)
	print(gaussian_img.shape, gaussian_img.dtype)
	mean_filter = cv2.blur(gaussian_img, (5,5))
	median_filter = cv2.medianBlur(gaussian_img, 5)
	images = [gaussian_img, mean_filter, median_filter]
	titles = ['gaussian_img', 'mean_filter', 'median_filter']
	for i in range(3):
		plt.subplot(1,3,i+1)
		plt.title(titles[i])
		plt.imshow(images[i])



	# denoise on salt and pepper noise
	plt.figure()
	salt_pepper_img = img_as_ubyte(salt_pepper_img)
	#salt_pepper_img = cv2.cvtColor(salt_pepper_img.astype(np.uint8), cv2.COLOR_RGB2BGR)

	mean_filter = cv2.blur(salt_pepper_img, (5,5))
	median_filter = cv2.medianBlur(salt_pepper_img, 5)
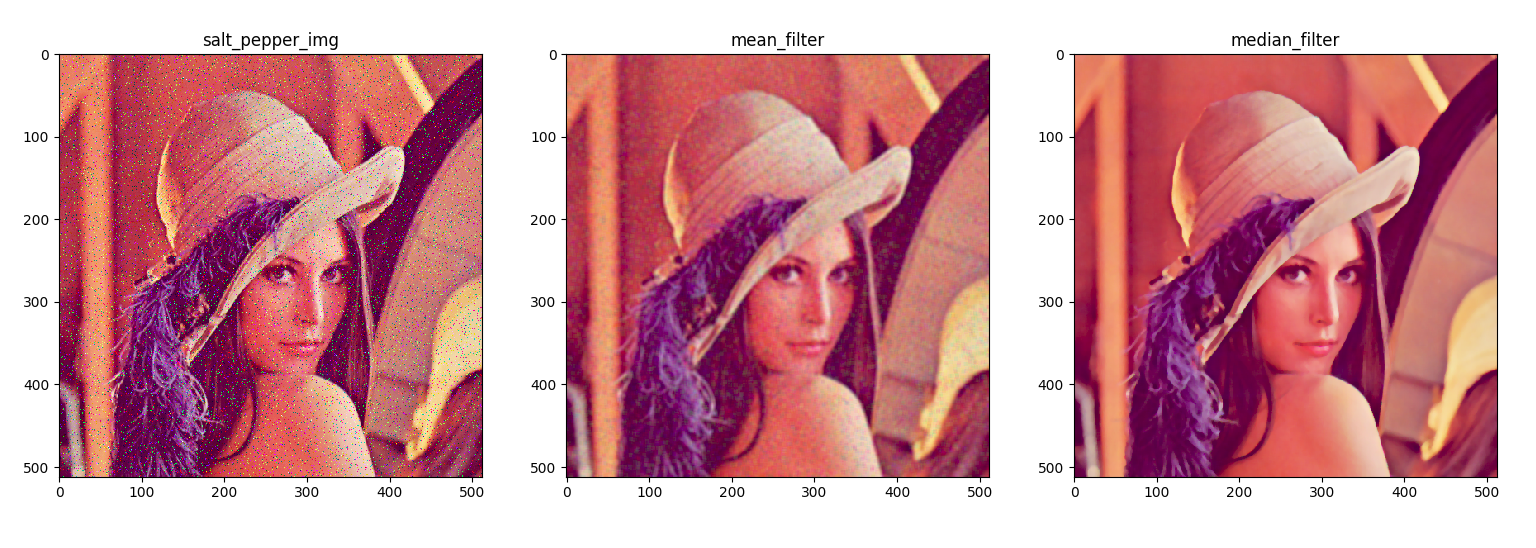
	images = [salt_pepper_img, mean_filter, median_filter]
	titles = ['salt_pepper_img', 'mean_filter', 'median_filter']
	for i in range(3):
		plt.subplot(1,3,i+1)
		plt.title(titles[i])
		plt.imshow(images[i])

	plt.show()
	plt.close('all')

 

 

 

双边滤波

加权均值滤波和高斯滤波是求中心点区域邻近区域像素的高斯加权平均值，只考虑了像素之间的空间关系，而没有考虑像素值之间的关系。而边界处的灰度值变化比较大，因此这两种方法也会把边界模糊掉。而双边滤波会同时使用空间高斯权重和灰度值相似性高斯权重，确保边界处不会被模糊掉。

 

import cv2
import matplotlib.pyplot as plt


img = cv2.imread('/home/vincent/Pictures/work/lena.png')

gaussian_img = cv2.GaussianBlur(img, (5,5), 75)


bilateral_img = cv2.bilateralFilter(img, 5, 75, 75)

images = [img, gaussian_img, bilateral_img]
titles = ['origin image', 'gaussian blur', 'bilateral blur']

for i in range(3):
	plt.subplot(1,3,i+1)
	plt.imshow(cv2.cvtColor(images[i], cv2.COLOR_BGR2RGB))
	plt.title(titles[i])
plt.show()

plt.close('all')

 

由上图可以看出双边滤波能够较好的保留图像的边缘信息。