数据结构算法基础-内部排序算法

1 arr = [1,23,12,9,8,8,9,1,1,8,] 2 def quickSortCore(arr,start,end): 3 if start < end: 4 index = partition(arr,start,end) 5 quickSortCore(arr,start,index-1) 6 quickSortCore(arr,index+1,end) 7 8 def partition(arr,start,end): 9 key = arr[start] 10 while(start < end): 11 while(start < end and key <= arr[end]): 12 end -= 1 13 if(start < end): 14 arr[start],arr[end] = arr[end],arr[start] 15 while(start < end and key >= arr[start]): 16 start += 1 17 if(start<end): 18 arr[start],arr[end] = arr[end],arr[start] 19 return start 20 quickSortCore(arr,0,len(arr)-1) 21 print(arr)

1 package com.sort; 2 3 public class QuickSortDemo { 4 public static void main(String[] args) { 5 int []arr = {8,9,8,8,9,1,1}; 6 QuickSortDemo q = new QuickSortDemo(); 7 q.quickSortCore(arr,0,arr.length-1); 8 for(int a : arr){ 9 System.out.print(a+" "); 10 } 11 } 12 private void quickSortCore(int[] arr, int start, int end) { 13 if(start<end){ 14 int sepIndex = partition(arr,start,end); 15 // System.out.println(sepIndex); 16 quickSortCore(arr, start, sepIndex-1); 17 quickSortCore(arr, sepIndex+1, end); 18 } 19 20 } 21 //分开 22 private int partition(int[] arr, int start, int end) { 23 int key = arr[start]; 24 int tmp = 0; 25 while(start < end){ 26 while((start < end) &&(key<= arr[end]) ){ 27 end --; 28 } 29 // 交换时,一定是 start 与 end 相交换 30 if(start<end){ 31 tmp = arr[end]; 32 arr[end] = arr[start]; 33 arr[start] = tmp; 34 start++; 35 } 36 while((start< end) &&(key>= arr[start])){ 37 start++; 38 } 39 if(start<end){ 40 tmp = arr[start]; 41 arr[start] = arr[end]; 42 arr[end] = tmp; 43 end--; 44 } 45 }// start == end 46 // arr[start] = key;// 可不加 47 return start; 48 } 49 50 }
注意:1) 交换时是 start 与 end 相交换,与 key是无关的。以上的代码应是最慢的quickSort; 2) 快排是不稳定的排序方法,空间复杂度为O(logN)
2、归并排序(稳定的排序方法,空间复杂度为O(n))

1 package com.sort; 2 3 import java.util.Arrays; 4 5 public class MergSortDemo { 6 public static void main(String[] args) { 7 int[] arr = { 8, 9, 8, 8, 9, 1, 1 }; 8 MergSortDemo m = new MergSortDemo(); 9 m.mergeSort(arr); 10 System.out.println(Arrays.toString(arr)); 11 } 12 13 public void mergeSort(int[] arr) { 14 int[] tmp = new int[arr.length]; 15 mergeSortCore(arr, 0, arr.length - 1, tmp); 16 } 17 18 public void mergeSortCore(int[] arr, int start, int end, int[] tmp) { 19 20 if (start < end) { 21 int mid = (end - start) / 2 + start; 22 mergeSortCore(arr, start, mid, tmp); 23 mergeSortCore(arr, mid+1, end, tmp); 24 merge(arr, start, mid , end); 25 } 26 } 27 28 // / arr[start...mid] 与 arr[mid+1,... end] ; 两个有序的子数组进行归并 29 private void merge(int[] arr, int start, int mid, int end) { 30 int s = start; 31 int m = mid + 1; 32 // int e = end; 33 int[] tmp = new int[end - start + 1]; 34 int index = 0; 35 // 处理共同的 36 while (s <= mid && m <= end) { 37 while (s <= mid && arr[s] <= arr[m]) { 38 tmp[index++] = arr[s++]; 39 } 40 while (m <= end && arr[s]> arr[m]) { 41 tmp[index++] = arr[m++]; 42 } 43 } 44 // 处理剩下的 45 while (s <= mid) { 46 tmp[index++] = arr[s++]; 47 } 48 while (m <= end) { 49 tmp[index++] = arr[m++]; 50 } 51 for (int i = start, j = 0; i <= end; i++) { 52 arr[i] = tmp[j++]; 53 } 54 } 55 56 }

1 def mergeSort(arr,start,end): 2 if start > end: 3 return 4 if(start < end): 5 mid = (end - start)//2 + start 6 mergeSort(arr,start,mid) 7 mergeSort(arr,mid+1,end) 8 merge(arr,start,mid,end) 9 10 def merge(arr,start,mid,end): 11 # i =start,j = mid+1 ## python 中千万不要这样赋值!! 12 i = start 13 j = mid + 1 14 # print(str(start) + '..'+ str(end)) 15 tmp = [] 16 while(i<=mid and j<=end): 17 if(arr[i] <= arr[j]): 18 tmp.append(arr[i]) 19 i = i+1 20 else: 21 tmp.append(arr[j]) 22 j = j + 1 23 if(i<= mid): 24 tmp.extend(arr[i:mid+1]) 25 if(j <= end): 26 tmp.extend(arr[j:end+1]) 27 arr[start:end+1] = tmp 28 del tmp 29 return arr 30 mergeSort(arr,0,len(arr)-1) 31 # merge(arr,0, (len(arr)-1)//2, len(arr)-1) 32 print(arr)
3、堆排序(不是稳定的排序方法)(下期)
扩展:
1)求数组中第K小的数
思想:利用快排的思想,随机选择元素 t , 它将数组分成两部分,小于 t 的 和大于 t 的; 分别计为 a[0...m-1] ; a[m+1,...n-1];
若 m = k -1 ;则返回 t ;
若 m> k-1 ,说明 第k小的值在a[0...m-1];则求a[0...m-1]中第K小的值;
若 m< k-1 ,说明 第k小的值在a[m+1,...n-1],则在a[m+1,...n-1] 求 k-m小的数。 // 在代码中应是与 下标相比较,所以左右都是K,都是K
平均时间复杂度O(N)

1 def getKthSmall(arr,start,end,k): 2 s = start 3 e = end 4 key = arr[s] 5 while(s < e): 6 while(s < e and key <= arr[e]): 7 e -= 1 8 if key > arr[e]: 9 arr[s] ,arr[e] = arr[e], arr[s] 10 while(s < e and key > arr[s]): 11 s += 1 12 if key < arr[s]: 13 arr[s], arr[e] = arr[e], arr[s] 14 print('start = %d; end = %d s = %d' % (start, end,s)) 15 if s == k-1: 16 return s 17 elif s > k-1: 18 return getKthSmall(arr,start,s-1,k) 19 else: 20 ## getKthSmall(arr,s+1,end, k-s-1), 不是这个,不是这个,不是这个, 21 ## 因为 我们是与下标比较,所以都是K, 22 return getKthSmall(arr,s+1,end,k) 23 24 arr = [33,3,4,6,32] 25 index = getKthSmall(arr,0,len(arr)-1,3) 26 print(arr[index])
2) 求数组中的逆序数问题
给定一个数组A[0,...N-1] ,若对于两个元素a[i],a[j] ,若 i<j 且 a[i] >a[j] ,则称(a[i],a[j])为逆序对。
如数组 2,56,2,7的逆序数为 3. 归并排序图解如下,在合并时,都可用来计算其逆序对的数。
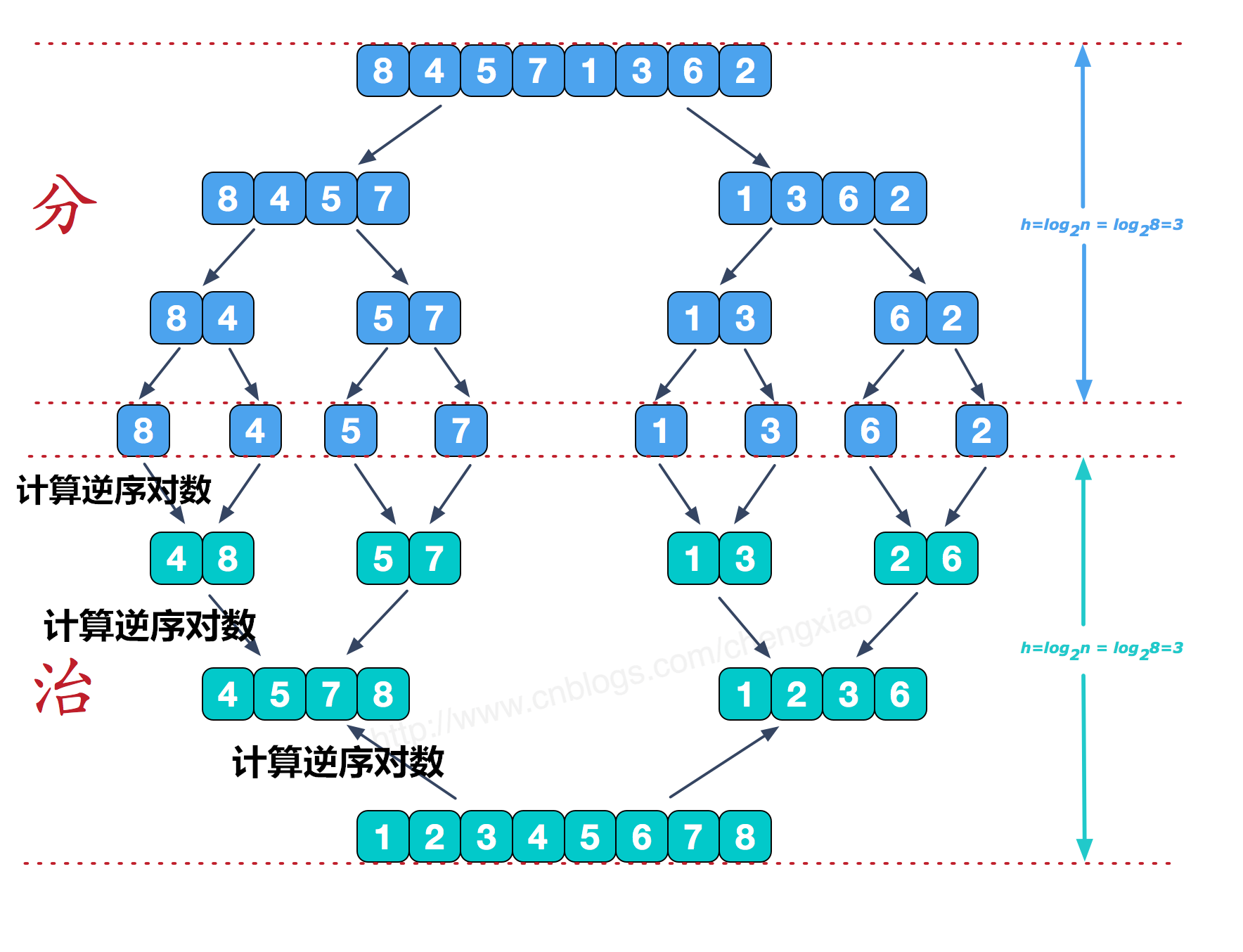

1 package com.sort; 2 3 public class 逆序对数 { 4 static Integer count = 0; 5 public static void main(String[] args) { 6 int[] arr = { 3, 56, 2, 7 }; 7 mergeSort(arr, 0, arr.length - 1); 8 System.out.println(count); 9 } 10 11 private static void mergeSort(int[] arr, int start, int end) { 12 if (start < end) { 13 int mid = (end - start) / 2 + start; 14 mergeSort(arr, start, mid); 15 mergeSort(arr, mid + 1, end); 16 merge(arr, start, mid, end); 17 } 18 } 19 20 private static void merge(int[] arr, int start, int mid, int end) { 21 // System.out.println(".......2............"); 22 int i = start, j = mid + 1; 23 int k = 0; 24 int[] tmp = new int[end - start + 1]; 25 while (i <= mid && j <= end) { 26 if (i <= mid && arr[i] < arr[j]) { // if (i <= mid && arr[i] <= arr[j]) 27 tmp[k++] = arr[i++]; 28 }else{ // if (j <= end && arr[i] > arr[j]) 29 count += (mid - i + 1); // 主要在这一块地方求!!,别注意条件,前没有=, 30 //这也很好理解,有等于号,也是有逆序数对的。 31 tmp[k++] = arr[j++]; 32 33 } 34 } 35 while (i <= mid) { 36 tmp[k++] = arr[i++]; 37 } 38 while (j <= end) { 39 tmp[k++] = arr[j++]; 40 } 41 k = 0; 42 for (int t = start; t <= end; t++) { 43 arr[t] = arr[k++]; 44 } 45 // System.out.println("..================............"); 46 } 47 48 }
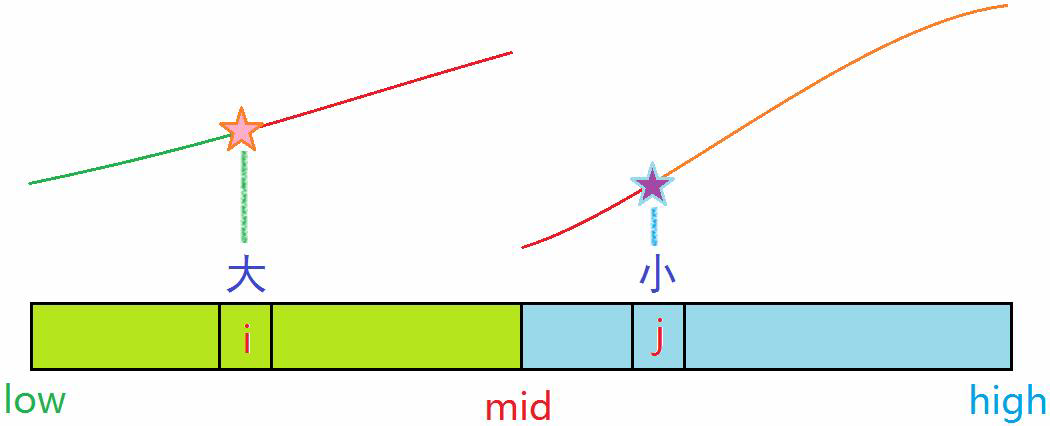
即,如下图所示,在求 逆序对时,两个有序合并时, count += (mid- i + 1);另要注意 arr[i] 等于 arr[j] 时,也是有逆序对的。注意 判断的条件!!
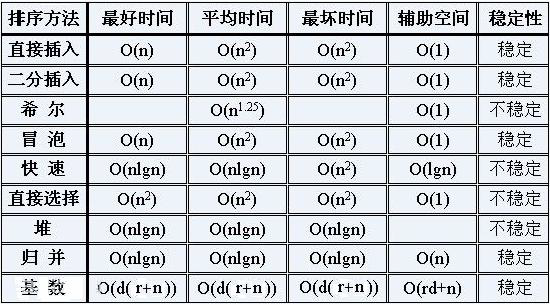
附其它O(n**2)的排序算法
直接插入排序(稳定的排序方法):

1 def straightInsertSort(arr): 2 for i in range(1,len(arr)): ## [1,....len(arr)-1 ]个元素 3 tmp = arr[i] 4 j = i -1 5 while j>=0 : ## 与 [i-1,....0]号元素相比较 6 if(arr[j]> tmp): 7 arr[j+1] = arr[j] 8 j = j-1 9 else: 10 break 11 ## 跳出时 j==0 或 arr[j] <= tmp 12 arr[j+1] = tmp
下期:堆排序,桶排序的运用
桶排序的运用: 数组的最大间隔
给定整数数组A[0...N-1],求这N个数排序后最大间隔。如1,7,14,9,4,13的最大减个为4。
排序后:1,4,7,9,13,14,最大间隔是13-9=4
显然,对原来数组排序,然后求后项减前项的最大值,即为解,但还有更好的方法。

1 package com.sort; 2 3 import java.util.ArrayList; 4 import java.util.Arrays; 5 6 //数组的最大间隔 7 8 class bucket { 9 int min = Integer.MAX_VALUE; 10 int max = Integer.MIN_VALUE; 11 // 对于新加入的数据,要加入到桶中, 12 // 桶中只要保留最大值与最小值就可以 13 void add(int num) { 14 min = Math.min(min, num); 15 max = Math.max(max, num); 16 } 17 @Override 18 public String toString() { 19 return "bucket [min=" + min + ", max=" + max + "]"; 20 } 21 } 22 23 public class 桶排序的应用 { 24 public static void main(String[] args) { 25 桶排序的应用 a = new 桶排序的应用(); 26 int []arr = {1,2,3,6,-9}; 27 // int[] arr = { 1, 7, 9, 4,14, 13 }; 28 System.out.println(a.calMaxGap(arr)); 29 } 30 31 public int calMaxGap(int[] arr) { 32 int max = arr[0]; 33 int min = arr[0]; 34 for (int i = 1; i < arr.length; i++) { 35 max = Math.max(max, arr[i]); 36 min = Math.min(min, arr[i]); 37 } 38 // 将数据放入桶中 39 int delta = max - min; 40 int nBucket = 0; // 桶的下标 41 // n 个桶 42 bucket[] pbucket = new bucket[arr.length]; 43 for (int i = 0; i < arr.length; i++) { 44 nBucket = ((arr[i] - min)* arr.length / delta) ; 45 if (nBucket >= arr.length) { // 只有n 个桶 46 nBucket = arr.length - 1; 47 } 48 if(pbucket[nBucket] == null){ 49 bucket tmp = new bucket(); 50 pbucket[nBucket] = tmp; 51 }// 防上 pbucket[nBucket] 为空指针异常 52 pbucket[nBucket].add(arr[i]); 53 System.out.println(Arrays.toString(pbucket)); 54 } 55 56 // 计算最大的间隔 57 int nGap = delta / arr.length; // 最小间隔 58 int gap = 0; 59 // 第一个桶一定是有用的; 因为 下标为 ((arr[i] - min)/delta)*arr.length ; 60 // arr[i] = min时,就放在第一个桶中 61 int i = 0; // i表示第一个有数据桶的下标 62 for (int j = 1; j < pbucket.length; j++) { 63 if (pbucket[j] != null) { //只用计算有数据的桶 64 gap = pbucket[j].min - pbucket[i].max; 65 nGap = Math.max(gap, nGap); 66 i = j; // i就是下一个有数据的桶 67 } 68 } 69 return nGap; 70 } 71 }

1 #!/usr/bin/python 2 # -*- coding: UTF-8 -*- 3 arr =[ 1, 7, 9,10, 4,14, 13] 4 def maxGap(arr): 5 buckets = [[None,None] for _ in arr] ## 准备好桶 6 print(buckets) 7 min_val, max_val = min(arr),max(arr) 8 # 将数据放入桶中 9 size = len(arr) 10 delta = max_val - min_val 11 for value in arr: 12 buck_index = (value - min_val)*size // delta 13 if buck_index == size: 14 buck_index = size -1 15 if buckets[buck_index][0] == None or buckets[buck_index][1] ==None: 16 buckets[buck_index][0] = value 17 buckets[buck_index][1] = value 18 else: 19 buckets[buck_index][0] = min(value,buckets[buck_index][0]) 20 buckets[buck_index][1] = max(value,buckets[buck_index][1]) 21 print(buckets) 22 # 求最大的间隔 23 max_gap = delta // len(arr) ## 平均分布时,间隔最小 24 i = 0 25 for j in range(len(buckets)): 26 if buckets[j][0] != None and buckets[j][1] != None: 27 gap = buckets[j][0] - buckets[i][1] 28 max_gap = max(max_gap, gap) 29 i = j 30 return max_gap 31 # max_gap = max( buckets[i][0] -buckets[i-1][1] for i in range(1,len(buckets)) ) 32 33 print(maxGap(arr))
下期: 跳跃链表(Skip List)
参考:
图解排序算法(四)之归并排序




 浙公网安备 33010602011771号
浙公网安备 33010602011771号