数据结构丨二叉搜索树

介绍

二叉搜索树是二叉树的一种特殊形式。 二叉搜索树具有以下性质：每个节点中的值必须大于（或等于）其左侧子树中的任何值，但小于（或等于）其右侧子树中的任何值。

我们将在本章中更详细地介绍二叉搜索树的定义，并提供一些与二叉搜索树相关的习题。

完成本卡片后，你将：

1. 理解二叉搜索树的性
2. 熟悉在二叉搜索树中的基本操作
3. 理解高度平衡二叉搜索树的概念

二叉搜索树的定义

二叉搜索树（BST）是二叉树的一种特殊表示形式，它满足如下特性：

1. 每个节点中的值必须大于（或等于）存储在其左侧子树中的任何值。
2. 每个节点中的值必须小于（或等于）存储在其右子树中的任何值。

下面是一个二叉搜索树的例子：

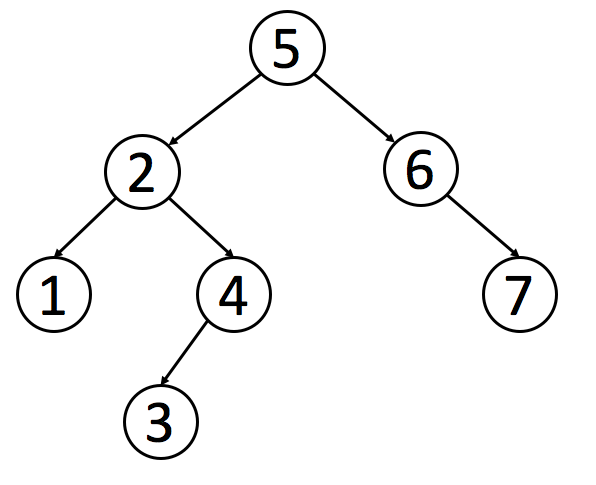
这篇文章之后，我们提供了一个习题来让你验证一个树是否是二叉搜索树。 你可以运用我们上述提到的性质来判断。 前一章介绍的递归思想也可能会对你解决这个问题有所帮助。

像普通的二叉树一样，我们可以按照前序、中序和后序来遍历一个二叉搜索树。 但是值得注意的是，对于二叉搜索树，我们可以通过中序遍历得到一个递增的有序序列。因此，中序遍历是二叉搜索树中最常用的遍历方法。

在文章习题中，我们也添加了让你求解二叉搜索树的中序 后继节点（in-order successor）的题目。显然，你可以通过中序遍历来找到二叉搜索树的中序后继节点。 你也可以尝试运用二叉搜索树的特性，去寻求更好的解决方案。

验证二叉搜索树

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

• 节点的左子树只包含小于当前节点的数。
• 节点的右子树只包含大于当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1:

输入:
    2
   / \
  1   3
输出: true

示例 2:

输入:
    5
   / \
  1   4
     / \
    3   6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
     根节点的值为 5 ，但是其右子节点值为 4 。

参考：https://www.cnblogs.com/grandyang/p/4298435.html

#include <iostream>
#include <vector>

using namespace std;

class TreeNode{
public: 
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(){};
    TreeNode(int x):val(x), left(NULL), right(NULL){};
};

// Recursion without inorder traversal
//这道验证二叉搜索树有很多种解法，可以利用它本身的性质来做，即左<根<右，也可以通过利用中序遍历结果为有序数列来做，下面我们先来看最简单的一种，就是利用其本身性质来做，初始化时带入系统最大值和最小值，在递归过程中换成它们自己的节点值，用long代替int就是为了包括int的边界条件，代码如下：
class SolutionA{
public:
    bool isValidBST(TreeNode* root){
        return isValidBST(root, LONG_MIN, LONG_MAX);
    }
    bool isValidBST(TreeNode* root, long mn, long mx){
        if(!root) return true;
        if(root->val <= mn || root->val >= mx) return false;
        return isValidBST(root->left, mn, root->val) && isValid(root->right, root->val, mx);
    }
};
//Recursion
//这题实际上简化了难度，因为有的时候题目中的二叉搜索树会定义为左<=根<右，而这道题设定为一般情况左<根<右，那么就可以用中序遍历来做。因为如果不去掉左=根这个条件的话，那么下边两个数用中序遍历无法区分：
class SolutionB{
public: 
    bool isValidBST(TreeNode* root){
        if(!root) return true;
        vector<int> vals;
        inorder(root, vals);
        for(int i=0; i<vals.size()-1; i++){
            if(vals[i] >= vals[i+1]) return false;
        }
        return true;
    }
    void inorder(TreeNode* root, vector<int>& vals){
        if(!root) return;
        inorder(root->left, vals);
        vals.push_back(root->val);
        inorder(root->right, vals);
    }
};

二叉搜索树迭代器

实现一个二叉搜索树迭代器。你将使用二叉搜索树的根节点初始化迭代器。

调用 next() 将返回二叉搜索树中的下一个最小的数。

示例：

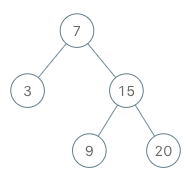
BSTIterator iterator = new BSTIterator(root);
iterator.next();    // 返回 3
iterator.next();    // 返回 7
iterator.hasNext(); // 返回 true
iterator.next();    // 返回 9
iterator.hasNext(); // 返回 true
iterator.next();    // 返回 15
iterator.hasNext(); // 返回 true
iterator.next();    // 返回 20
iterator.hasNext(); // 返回 false

提示：

• next() 和 hasNext() 操作的时间复杂度是 O(1)，并使用 O(h) 内存，其中 h 是树的高度。
• 你可以假设 next() 调用总是有效的，也就是说，当调用 next() 时，BST 中至少存在一个下一个最小的数。

参考：https://www.cnblogs.com/grandyang/p/4231455.html

#include <iostream>
#include <stack>

using namespace std;

class TreeNode{
public: 
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(){};
    TreeNode(int x):val(x), left(NULL), right(NULL){};
};

class BSTIterator{
private: 
    stack<TreeNode*> s;
public: 
    BSTIterator(TreeNode* root){
        while(root){
            s.push(root);
            root = root->left;
        }
    }
    bool hasNext(){
        return !s.empty();
    }
    int next(){
        TreeNode* n = s.top();
        s.pop();
        int res = n->val;
        if(n->right){
            n = n->right;
            while(n){
                s.push(n);
                n = n->left;
            }
        }
        return res;
    }
};

int main(){
    return 0;
}

二叉搜索树中的基本操作

在二叉搜索树中实现搜索操作

二叉搜索树主要支持三个操作：搜索、插入和删除。 在本章中，我们将讨论如何在二叉搜索树中搜索特定的值。

根据BST的特性，对于每个节点：

1. 如果目标值等于节点的值，则返回节点;
2. 如果目标值小于节点的值，则继续在左子树中搜索;
3. 如果目标值大于节点的值，则继续在右子树中搜索。

我们一起来看一个例子：我们在上面的二叉搜索树中搜索目标值为 4 的节点。

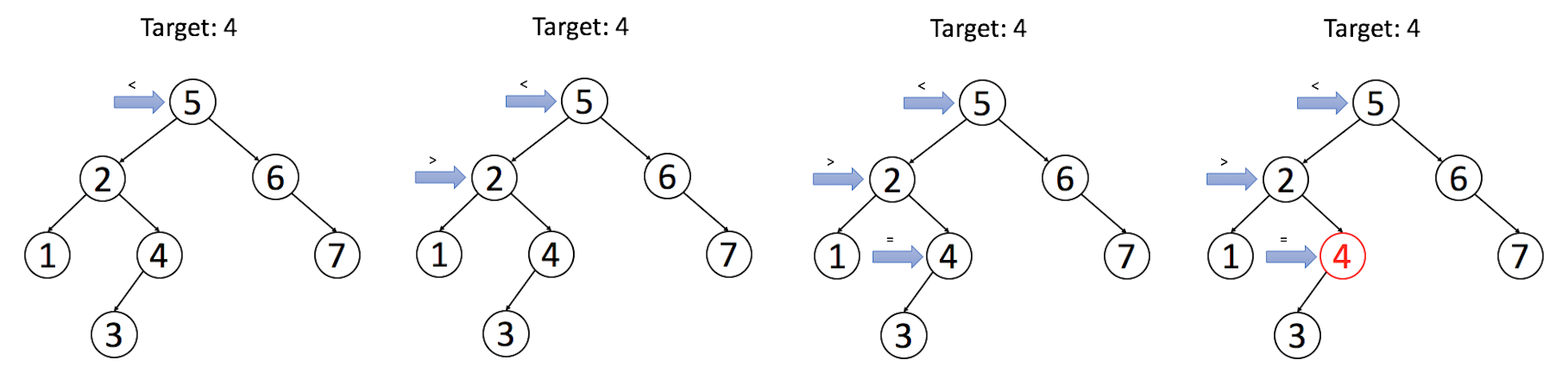
请在以下习题中，自己尝试实现搜索操作。 你可以运用递归或迭代方法去解决这类问题，并尝试分析时间复杂度和空间复杂度。我们将在之后的文章介绍一个更好的解决方案。

Search in a Binary Search Tree

给定二叉搜索树（BST）的根节点和一个值。 你需要在BST中找到节点值等于给定值的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 NULL。

例如，

给定二叉搜索树:

        4
       / \
      2   7
     / \
    1   3

和值: 2

你应该返回如下子树:

      2     
     / \   
    1   3

在上述示例中，如果要找的值是 5，但因为没有节点值为 5，我们应该返回 NULL。

参考https://www.cnblogs.com/grandyang/p/9912434.html

#include <iostream>

using namespace std;

class TreeNode{
public: 
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(){};
    TreeNode(int n):val(x),left(NULL),right(NULL);
};

//Recursion
class SolutionA{
public: 
    TreeNode* searchBST(TreeNode* root, int val){
        if(!root) return NULL;
        if(root->val == val) return root;
        return (root->val > val)? searchBST(root->left, val):searchBST(root->right, val);
    }
};

//Non-recursion
class SolutionB{
public: 
    TreeNode* searchBST(TreeNode* root, int val){
        while(root && root->val != val){
            root = (root->val > val)? root->left:root->right;
        }
        return root;
    }
};

在二叉搜索树中实现插入操作 - 介绍

二叉搜索树中的另一个常见操作是插入一个新节点。有许多不同的方法去插入新节点，这篇文章中，我们只讨论一种使整体操作变化最小的经典方法。 它的主要思想是为目标节点找出合适的叶节点位置，然后将该节点作为叶节点插入。 因此，搜索将成为插入的起始。

与搜索操作类似，对于每个节点，我们将：

1. 根据节点值与目标节点值的关系，搜索左子树或右子树；
2. 重复步骤 1 直到到达外部节点；
3. 根据节点的值与目标节点的值的关系，将新节点添加为其左侧或右侧的子节点。

这样，我们就可以添加一个新的节点并依旧维持二叉搜索树的性质。

我们来看一个例子：

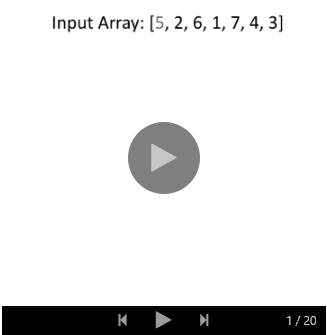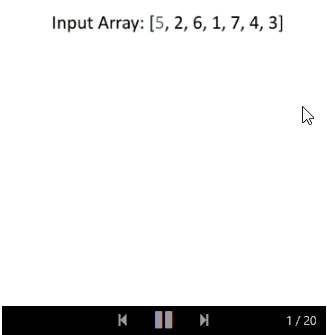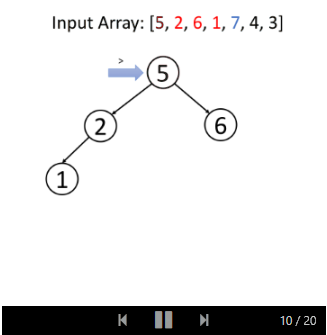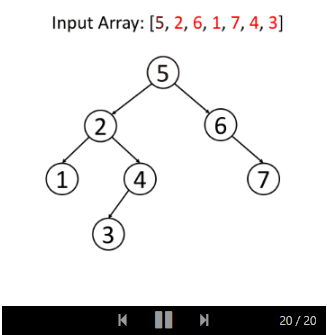
与搜索操作相同，我们可以递归或迭代地进行插入。 它的解决方案也与搜索非常相似，你应该可以自己实现，并以相同的方式分析算法的时间复杂度和空间复杂度。

Insert into a Binary Search Tree

给定二叉搜索树（BST）的根节点和要插入树中的值，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 保证原始二叉搜索树中不存在新值。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回任意有效的结果。

例如,

给定二叉搜索树:

        4
       / \
      2   7
     / \
    1   3

和 插入的值: 5

你可以返回这个二叉搜索树:

         4
       /   \
      2     7
     / \   /
    1   3 5

或者这个树也是有效的:

         5
       /   \
      2     7
     / \   
    1   3
         \
          4

#include <iostream>

using namespace std;

class TreeNode{
public: 
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(){};
    TreeNode(int n):val(n),left(NULL),right(NULL){};
};

//Recursion
class SolutionA{
public: 
    TreeNode* insertIntoBST(TreeNode* root, int val){
        if(!root) return new TreeNode(val);
        if(root->val > val) root->left = insertIntoBST(root->left, val);
        else root->right = insertIntoBST(root->right, val);
        return root;
    }
};

//Non-Recursion
class SolutionB{
public: 
    TreeNode* insertIntoBST(TreeNode* root, int val){
        if(!root) return new TreeNode(val);
        TreeNode* cur = root;
        while(true){
            if(cur->val > val){
                if(!cur->left) {cur->left = new TreeNode(val); break;
                cur = cur->left;}
            }else{
                if(!cur->right) {cur->right=new TreeNode(val); break;
                cur = cur->right;}
            }
        }
        return root;
    }
};

在二叉搜索树中实现删除操作

删除要比我们前面提到过的两种操作复杂许多。有许多不同的删除节点的方法，这篇文章中，我们只讨论一种使整体操作变化最小的方法。我们的方案是用一个合适的子节点来替换要删除的目标节点。根据其子节点的个数，我们需考虑以下三种情况：

1. 如果目标节点没有子节点，我们可以直接移除该目标节点。
2. 如果目标节只有一个子节点，我们可以用其子节点作为替换。
3. 如果目标节点有两个子节点，我们需要用其中序后继节点或者前驱节点来替换，再删除该目标节点。

我们来看下面这几个例子，以帮助你理解删除操作的中心思想：

例 1：目标节点没有子节点

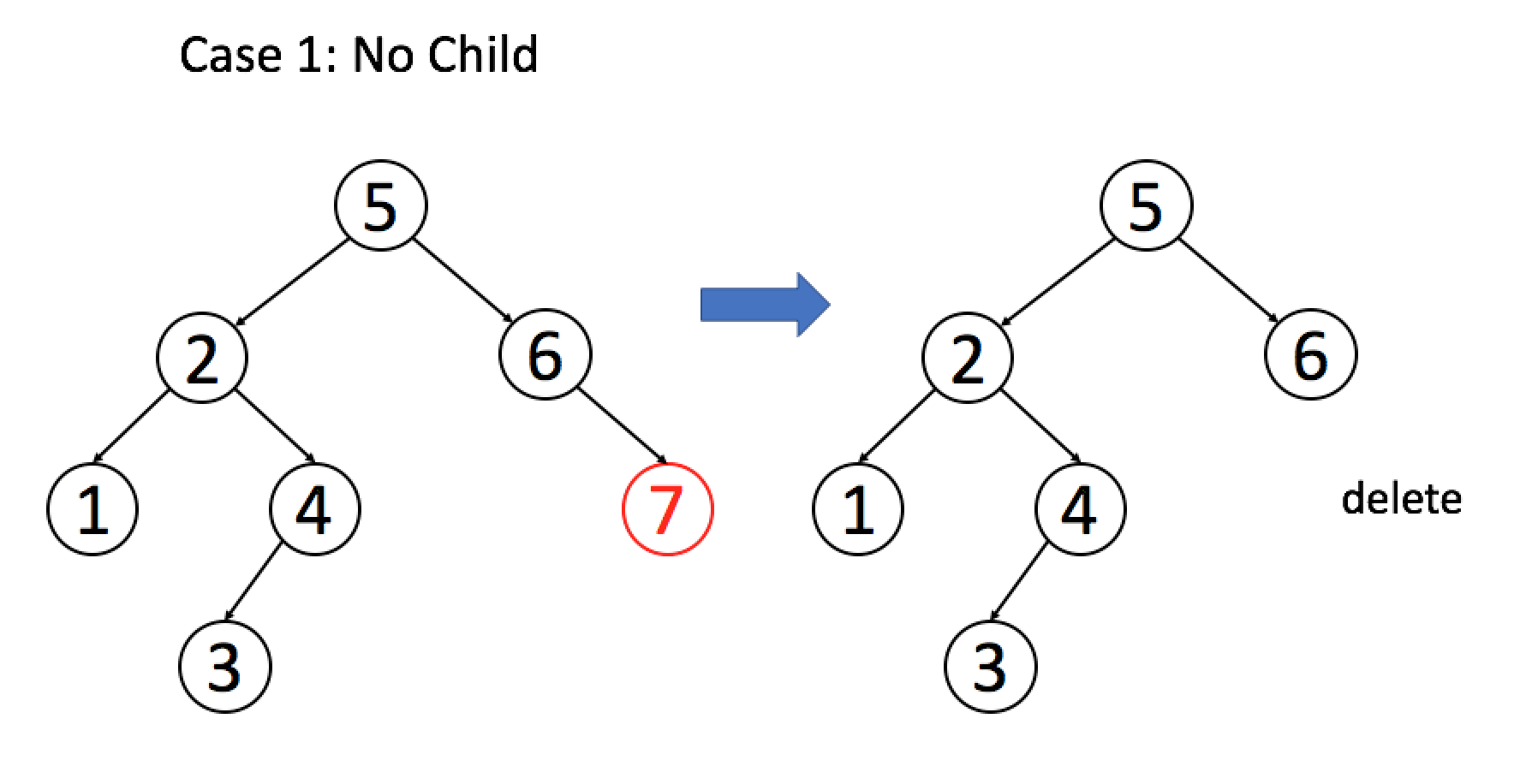
例 2：目标节只有一个子节点

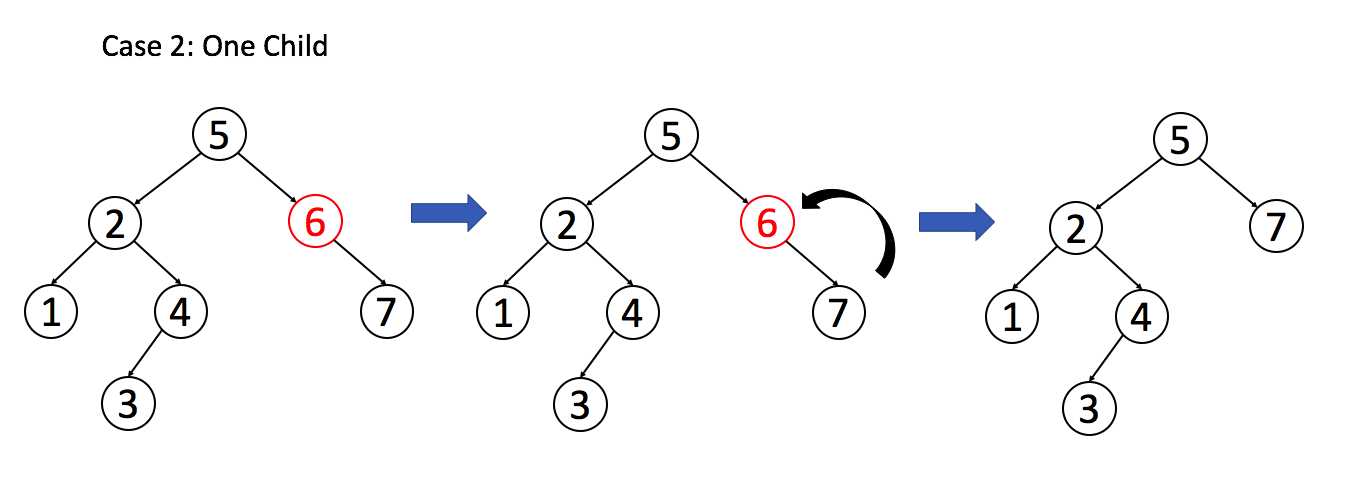
例 3：目标节点有两个子节点

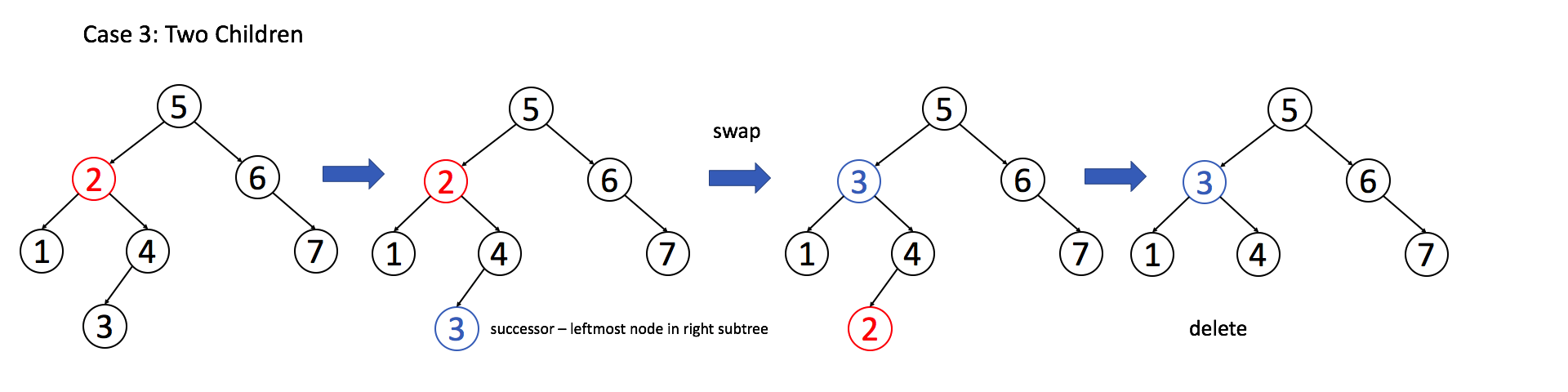
通过理解以上的示例，你应该可以独立实现删除操作了。

Delete Node in a BST

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

1. 首先找到需要删除的节点；
2. 如果找到了，删除它。

说明： 要求算法时间复杂度为 O(h)，h 为树的高度。

示例:

root = [5,3,6,2,4,null,7]
key = 3

    5
   / \
  3   6
 / \   \
2   4   7

给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。

一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。

    5
   / \
  4   6
 /     \
2       7

另一个正确答案是 [5,2,6,null,4,null,7]。

    5
   / \
  2   6
   \   \
    4   7

参考https://www.cnblogs.com/grandyang/p/6228252.html

#include <iostream>

using namespace std;

class TreeNode{
public: 
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(){};
    TreeNode(int n):val(n),left(NULL),right(NULL){};
};

//Recursion
//我们先来看一种递归的解法，首先判断根节点是否为空。由于BST的左<根<右的性质，使得我们可以快速定位到要删除的节点，我们对于当前节点值不等于key的情况，根据大小关系对其左右子节点分别调用递归函数。若当前节点就是要删除的节点，我们首先判断是否有一个子节点不存在，那么我们就将root指向另一个节点，如果左右子节点都不存在，那么root就赋值为空了，也正确。难点就在于处理左右子节点都存在的情况，我们需要在右子树找到最小值，即右子树中最左下方的节点，然后将该最小值赋值给root，然后再在右子树中调用递归函数来删除这个值最小的节点，参见代码如下：
class SolutionA{
public: 
    TreeNode* deleteNode(TreeNode* root, int key){
        if(!root) return NULL;
        if(root->val > key){
            root->left = deleteNode(root->left, key);
        }else if(root->val < key){
            root->right = deleteNode(root->right, key);
        }else{  //找到待删节点
            if(!root->left || !root->right){    //Case 1 & Case 2
                root = (root->left)? root->left : root->right;
            }else{//先往右一次 然后一直往左下 从而找到比root略大的节点
                TreeNode* cur = root->right;
                while(cur->left) cur = cur->left;
                root->val = cur->val;
                root->right = deleteNode(root->right, cur->val);//需要重新排序
            }
        }
    }
};

//下面我们来看迭代的写法，还是通过BST的性质来快速定位要删除的节点，如果没找到直接返回空。遍历的过程要记录上一个位置的节点pre，如果pre不存在，说明要删除的是根节点，如果要删除的节点在pre的左子树中，那么pre的左子节点连上删除后的节点，反之pre的右子节点连上删除后的节点。在删除函数中，如果左右子节点都不存在，那么返回空；如果有一个不存在，那么我们返回那个存在的；难点还是在于处理左右子节点都存在的情况，还是要找到需要删除节点的右子树中的最小值，然后把最小值赋值给要删除节点，然后就是要处理最小值可能存在的右子树的连接问题，如果要删除节点的右子节点没有左子节点了的话，那么最小值的右子树直接连到要删除节点的右子节点上即可(因为此时原本要删除的节点的值已经被最小值替换了，所以现在其实是要删掉最小值节点)。否则我们就把最小值节点的右子树连到其父节点的左子节点上。文字表述确实比较绕，请大家自行带例子一步一步观察就会很清晰明了了，参见代码如下：
class SolutionB {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        TreeNode *cur = root, *pre = NULL;
        while (cur) {
            if (cur->val == key) break;
            pre = cur;
            if (cur->val > key) cur = cur->left;
            else cur = cur->right;
        }
        if (!cur) return root;
        if (!pre) return del(cur);
        if (pre->left && pre->left->val == key) pre->left = del(cur);
        else pre->right = del(cur);
        return root;
    }
    TreeNode* del(TreeNode* node) {
        if (!node->left && !node->right) return NULL;
        if (!node->left || !node->right) {
            return (node->left) ? node->left : node->right;
        }
        TreeNode *pre = node, *cur = node->right;
        while (cur->left) {
            pre = cur;
            cur = cur->left;
        }
        node->val = cur->val;
        (pre == node ? node->right : pre->left) = cur->right;
        return node;
    }
};

//下面来看一种对于二叉树通用的解法，适用于所有二叉树，所以并没有利用BST的性质，而是遍历了所有的节点，然后删掉和key值相同的节点，参见代码如下：
class SolutionC{
public: 
    TreeNode* deleteNode(TreeNode* root, int key){
        if(!root) return NULL;
        if(root->val == key){
            if(!root->right) return root->left;
            else{
                TreeNode* cur = root->right;
                while(cur->left) cur = cur->left;
                swap(root->val, cur->val);
            }
        }
        root->left = deleteNode(root->left, key);
        root->right = deleteNode(root->right, key);
        return root;
    }
};

小结

二叉搜索树简介 - 小结

我们已经介绍了二叉搜索树的相关特性，以及如何在二叉搜索树中实现一些基本操作，比如搜索、插入和删除。熟悉了这些基本概念之后，相信你已经能够成功运用它们来解决二叉搜索树问题。

二叉搜索树的有优点是，即便在最坏的情况下，也允许你在O(h)的时间复杂度内执行所有的搜索、插入、删除操作。

通常来说，如果你想有序地存储数据或者需要同时执行搜索、插入、删除等多步操作，二叉搜索树这个数据结构是一个很好的选择。

一个例子

问题描述：设计一个类，求一个数据流中第k大的数。

一个很显而易见的解法是，先将数组降序排列好，然后返回数组中第k个数。

但这个解法的缺点在于，为了在O(1)时间内执行搜索操作，每次插入一个新值都需要重新排列元素的位置。从而使得插入操作的解法平均时间复杂度变为O(N)。因此，算法总时间复杂度会变为O(N^2)。

鉴于我们同时需要插入和搜索操作，为什么不考虑使用一个二叉搜索树结构存储数据呢？

我们知道，对于二叉搜索树的每个节点来说，它的左子树上所有结点的值均小于它的根结点的值，右子树上所有结点的值均大于它的根结点的值。

换言之，对于二叉搜索树的每个节点来说，若其左子树共有m个节点，那么该节点是组成二叉搜索树的有序数组中第m + 1个值。

你可以先独立思考这个问题。请先尝试把多个节点存储到树中。你可能还需要在每个节点中放置一个计数器，以计算以此节点为根的子树中有多少个节点。

如果你仍然不清楚解法的思想，我们会提供一个示例动画：

1. 插入

2. 搜索

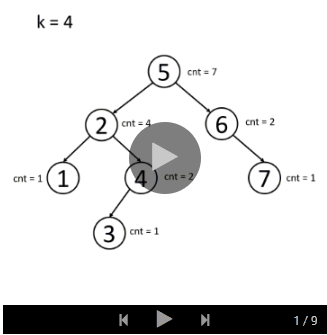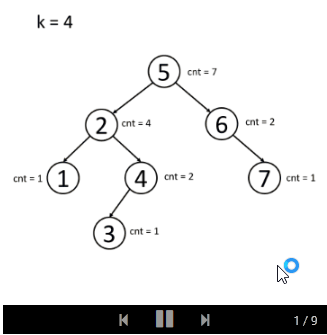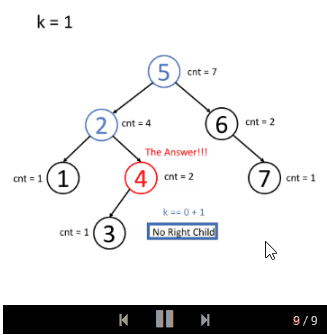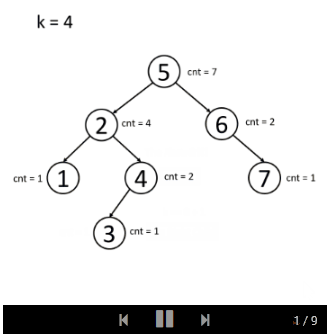
Kth Largest Element in a Stream

设计一个找到数据流中第K大元素的类（class）。注意是排序后的第K大元素，不是第K个不同的元素。

你的 KthLargest 类需要一个同时接收整数 k 和整数数组nums 的构造器，它包含数据流中的初始元素。每次调用 KthLargest.add，返回当前数据流中第K大的元素。

说明:
你可以假设 nums 的长度≥ k-1 且k ≥ 1。

参考：https://www.cnblogs.com/grandyang/p/9941357.html

#include <iostream>
#include <queue>
#include <vector>

using namespace std;

//这道题让我们在数据流中求第K大的元素，跟之前那道Kth Largest Element in an Array很类似，但不同的是，那道题的数组是确定的，不会再增加元素，这样确定第K大的数字就比较简单。而这道题的数组是不断在变大的，所以每次第K大的数字都在不停的变化。那么我们其实只关心前K大个数字就可以了，所以我们可以使用一个最小堆来保存前K个数字，当再加入新数字后，最小堆会自动排序，然后把排序后的最小的那个数字去除，则堆中还是K个数字，返回的时候只需返回堆顶元素即可，参见代码如下：
class KthLargest{
private:
    //使用了优先队列，greater从小到大，less泽从大到小。
    priority_queue<int, vector<int>, greater<int>> q;
    int K;
public: 
    KthLargest(int k, vector<int> nums){
        for(int num: nums){
            q.push(num);
            //丢掉小的数字，因为小的数在插入新的数字后只可能出现在>=k的位置
            //若插入大的数，则可以将最小的数字丢弃，因为其不会再被索引到
            if(q.size() > k) q.pop();
        }
        K = k;
    }
    int add(int val){
        q.push(val);
        if(q.size() > K) q.pop();
        //因为优先队列从小到大放置，所以第k大的元素就相当于在前k最大中选择最小的
        return q.top(); 
    }
};

二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

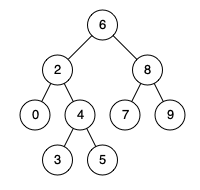
示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

• 所有节点的值都是唯一的。
• p、q 为不同节点且均存在于给定的二叉搜索树中。

#include <iostream>

using namespace std;

class TreeNode{
public:
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(){};
    TreeNode(int x):val(x),left(NULL),right(NULL){};
};

//利用二叉搜索树的性质简化
class Solution{
public: 
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q){
        //往下过程中，先遇到p或者q，就是最近祖先
        if(root==NULL || root==p || root==q)
            return root;
        if(p->val < root->val && q->val< root->val)
            return lowestCommonAncestor(root->left, p, q);
        else if(p->val > root->val && q->val > root->val)
            return lowestCommonAncestor(root->right, p, q);
        else    //val一大一小就是自身。
            return root;
    }
};

存在重复元素 III

给定一个整数数组，判断数组中是否有两个不同的索引 i 和 j，使得 nums [i] 和 nums [j] 的差的绝对值最大为 t，并且 i 和 j 之间的差的绝对值最大为 ķ。

示例 1:

输入: nums = [1,2,3,1], k = 3, t = 0
输出: true

示例 2:

输入: nums = [1,0,1,1], k = 1, t = 2
输出: true

示例 3:

输入: nums = [1,5,9,1,5,9], k = 2, t = 3
输出: false

#include <iostream>
#include <vector>
#include <set>

using namespace std;

//思路：维持一个大小为k的窗口，由左向右在nums中移动。对于nums[i]，只要查找其之前的元素中是否存在大小范围在[nums[i] - t,nums[i] + t]的元素，如果存在就返回true。还要注意整数的溢出问题，比如下面的测试用例：
class Solution {
public:
    bool containsNearbyAlmostDuplicate(vector<int>& nums, int k, int t) {
        set<long long> record;
        for(int i = 0; i < nums.size(); i++){
            //lower_bound(val)返回set中大于或等于val的第一个元素位置。如果所有元素都小于val，则返回last的位置
            if(record.lower_bound((long long)nums[i] - (long long)t)  != record.end()   //record中是否存在大于 nums[i] - t的数?
                   && (long long)*record.lower_bound((long long)nums[i] - (long long)t) <= (long long)nums[i] + (long long)t)   //record中是否存在小于 nums[i] + t的数?
                return true;

            record.insert(nums[i]);
            if(record.size() > k)
                record.erase(nums[i - k]);
        }
        return false;
    }
};

int main(){
    vector<int> v = {1,2,3,1};
    Solution a = Solution();
    if(a.containsNearbyAlmostDuplicate(v, 3, 0))
        cout << "true";
    else
        cout << "false";
}

附录：高度平衡的二叉搜索树

高度平衡的二叉搜索树简介

在这篇文章中，我们将帮助你理解高度平衡的二叉搜索树的基本概念。

什么是一个高度平衡的二叉搜索树?

---

树结构中的常见用语:

• 节点的深度 - 从树的根节点到该节点的边数
• 节点的高度 - 该节点和叶子之间最长路径上的边数
• 树的高度 - 其根节点的高度

一个高度平衡的二叉搜索树（平衡二叉搜索树）是在插入和删除任何节点之后，可以自动保持其高度最小。也就是说，有N个节点的平衡二叉搜索树，它的高度是logN。并且，每个节点的两个子树的高度不会相差超过1。

• 为什么是logN呢?

下面是一个普通二叉搜索树和一个高度平衡的二叉搜索树的例子:

根据定义, 我们可以判断出一个二叉搜索树是否是高度平衡的 (平衡二叉树)。

正如我们之前提到的, 一个有*N*个节点的平衡二搜索叉树的高度总是logN。因此，我们可以计算节点总数和树的高度，以确定这个二叉搜索树是否为高度平衡的。

同样，在定义中， 我们提到了高度平衡的二叉树一个特性: 每个节点的两个子树的深度不会相差超过1。我们也可以根据这个性质，递归地验证树。

为什么需要用到高度平衡的二叉搜索树?

---

我们已经介绍过了二叉树及其相关操作, 包括搜索、插入、删除。 当分析这些操作的时间复杂度时，我们需要注意的是树的高度是十分重要的考量因素。以搜索操作为例，如果二叉搜索树的高度为*h*，则时间复杂度为*O(h)*。二叉搜索树的高度的确很重要。

所以，我们来讨论一下树的节点总数N和高度*h*之间的关系。 对于一个平衡二叉搜索树, 我们已经在前文中提过, 但对于一个普通的二叉搜索树， 在最坏的情况下, 它可以退化成一个链。

因此，具有N个节点的二叉搜索树的高度在logN到N区间变化。也就是说，搜索操作的时间复杂度可以从logN变化到N。这是一个巨大的性能差异。

所以说，高度平衡的二叉搜索树对提高性能起着重要作用。

如何实现一个高度平衡的二叉搜索树?

---

有许多不同的方法可以实现。尽管这些实现方法的细节有所不同，但他们有相同的目标:

1. 采用的数据结构应该满足二分查找属性和高度平衡属性。
2. 采用的数据结构应该支持二叉搜索树的基本操作，包括在O(logN)时间内的搜索、插入和删除，即使在最坏的情况下也是如此。

我们提供了一个常见的的高度平衡二叉树列表供您参考：

• 红黑树
• AVL树
• 伸展树
• 树堆

我们不打算在本文中展开讨论这些数据结构实现的细节。

高度平衡的二叉搜索树的实际应用

---

高度平衡的二叉搜索树在实际中被广泛使用，因为它可以在O(logN)时间复杂度内执行所有搜索、插入和删除操作。

平衡二叉搜索树的概念经常运用在Set和Map中。 Set和Map的原理相似。 我们将在下文中重点讨论Set这个数据结构。

Set(集合)是另一种数据结构，它可以存储大量key(键)而不需要任何特定的顺序或任何重复的元素。 它应该支持的基本操作是将新元素插入到Set中，并检查元素是否存在于其中。

通常，有两种最广泛使用的集合：散列集合(Hash Set)和树集合(Tree Set)。

树集合, Java中的Treeset或者C++中的set，是由高度平衡的二叉搜索树实现的。因此，搜索、插入和删除的时间复杂度都是O(logN)。

散列集合, Java中的HashSet或者C++中的unordered_set，是由哈希实现的, 但是平衡二叉搜索树也起到了至关重要的作用。当存在具有相同哈希键的元素过多时，将花费O(N)时间复杂度来查找特定元素，其中N是具有相同哈希键的元素的数量。 通常情况下，使用高度平衡的二叉搜索树将把时间复杂度从 O(N) 改善到 O(logN)。

哈希集和树集之间的本质区别在于树集中的键是有序的。

总结

---

高度平衡的二叉搜索树是二叉搜索树的特殊表示形式，旨在提高二叉搜索树的性能。但这个数据结构具体的实现方式，超出了我们这章的内容，也很少会在面试中被考察。但是了解高度平衡二叉搜索树的的基本概念，以及如何运用它帮助你进行算法设计是非常有用的。

平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。

示例 1:

给定二叉树 [3,9,20,null,null,15,7]

    3
   / \
  9  20
    /  \
   15   7

返回 true 。

示例 2:

给定二叉树 [1,2,2,3,3,null,null,4,4]

       1
      / \
     2   2
    / \
   3   3
  / \
 4   4

返回 false 。

参考https://www.cnblogs.com/simplekinght/p/9219697.html

class Solution{
public:
    int judge(TreeNode* root, bool &ans){
        if(root){
            int ans1 = judge(root->left, ans);
            int ans2 = judge(root->right, ans);
            if(abs(ans1-ans2)>1) ans=false;
            return max(ans1, ans2) + 1;
        }
        else return 0;
    }
    bool isBalanced(TreeNode* root){
        bool ans = true;
        judge(root, ans);
        return ans;
    }
};

将有序数组转换为二叉搜索树

将一个按照升序排列的有序数组，转换为一棵高度平衡二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。

示例:

给定有序数组: [-10,-3,0,5,9],

一个可能的答案是：[0,-3,9,-10,null,5]，它可以表示下面这个高度平衡二叉搜索树：

      0
     / \
   -3   9
   /   /
 -10  5

参考https://www.cnblogs.com/grandyang/p/4295618.html

#include <iostream>
#include <vector>

using namespace std;

class TreeNode{
public: 
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(){};
    TreeNode(int n):val(n),left(NULL),right(NULL){};
};

//这道题是要将有序数组转为二叉搜索树，所谓二叉搜索树，是一种始终满足左<根<右的特性，如果将二叉搜索树按中序遍历的话，得到的就是一个有序数组了。那么反过来，我们可以得知，根节点应该是有序数组的中间点，从中间点分开为左右两个有序数组，在分别找出其中间点作为原中间点的左右两个子节点，这不就是是二分查找法的核心思想么。所以这道题考的就是二分查找法，代码如下：
class SolutionA{
public: 
    TreeNode* sortedArrayToBST(vector<int>& nums){
        return helper(nums, 0, (int)nums.size()-1);
    }
    TreeNode* helper(vector<int>& nums, int left, int right){
        if(left > right) return NULL;
        int mid = left + (right-left) /2 ;
        TreeNode* cur = new TreeNode(nums[mid]);
        cur->left = helper(nums, left, mid-1);
        cur->right = helper(nums, mid+1, right);
        return cur;
    }
};

//我们也可以不使用额外的递归函数，而是在原函数中完成递归，由于原函数的参数是一个数组，所以当把输入数组的中间数字取出来后，需要把所有两端的数组组成一个新的数组，并且分别调用递归函数，并且连到新创建的cur结点的左右子结点上面，参见代码如下：
class SolutionB{
public: 
    TreeNode* sortedArrayToBST(vector<int>& nums){
        if(nums.empty()) return NULL;
        int mid = nums.size() / 2;
        TreeNode* cur = new TreeNode(nums[mid]);
        vector<int> left(nums.begin(), nums.begin()+mid), right(nums.begin() + mid+1, nums.end());
        cur->left = sortedArrayToBST(left);
        cur->right = sortedArrayToBST(right);
        return cur;
    }
};