什么是递归
一、函数递归 recursion
什么是递归:
函数直接或者间接的调用自身
示例:直接调用自身------死递归
def f(): f() f() print("递归完成") 执行结果: RecursionError: maximum recursion depth exceeded
示例:间接调用自身------死递归
def fa(): fb() def fb(): fa() fa() 执行结果: RecursionError: maximum recursion depth exceeded
递归说明:
1。 递归一定要控制递归层数,当符合某一条件时要终止递归
2。几乎所有的递归都能用循环来代替(重复的做一些事,规则相同,可用递归)
3。所有的循环都可以用递归做
4。循环对于整个运算的过程要非常清楚,而递归只要知道第N步和第N-1步直接的关系,实际上是一种数学归纳法的体现
a) 循环需要知道an 和n的关系,然后循环求解 (这个需要数学归纳法来求解出等式)
b) 递归只需要知道an 和 an-1 的关系就可以
补充:
数学归纳法的基本步骤分两步:
- 证明当n= 1时命题成立。
- 假设n=m时命题成立,那么可以推导出在n=m+1时命题也成立。(m代表任意自然数)
对于递归的计算的实现的理解
举例:
def fn(n): print("现在是第",n,"层递归") if n >= 3: return fn(n+1) print("递归的第",n,"层结束") fn(1) 执行结果: 现在是第 1 层递归 现在是第 2 层递归 现在是第 3 层递归 递归的第 2 层结束 递归的第 1 层结束
用图的方式理解计算机如何实现递归的
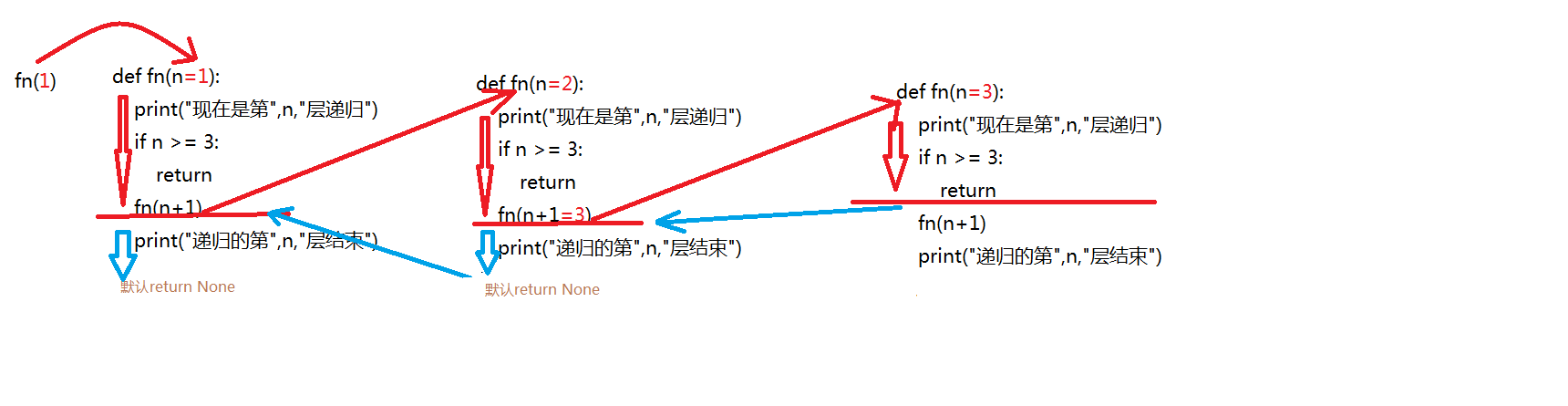
以上的递归实现的过程
递归也要区分真递归和假递归
用n!的求解举例 :
第一种方法:
an =n!=n*(n-1)*(n-2)*......*5*4*3*2*1
由于可以直接找到an 和 n的关系
s=1 n=eval(input()) for i in range(n): s=s*i print(s)
>>>3
>>>6
由于前面提到循环都可以用递归解决,可以变成递归如下:
def fac(n,s=1): if n==1: return s return fac(n-1,s*n) print(fac(3))
>>>6
尚未写的细一点一点, 便于理解
s=1 def fac(n): global s if n==1: return s s=s*n n=n-1 return fac(n) print(fac(3))
然而这是一个假递归, 只是把循环变成了递归而已
第二种
def fac(n): if n==1: return 1 return n*fac(n-1) print(fac(3)) >>>6
这个才是真递归,是通过
an = an-1 * n 的递归方式求出解
以上是我对 递归的理解


