杨辉三角(二项式定理)&&组合数 【noip 2011/2016 d2t1】

杨辉三角与二项式定理

，

 

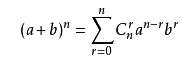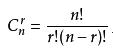
（紫书p349）

杨辉三角性质via百度百科

杨辉三角与组合数

 

 

EG1 noip2011 d2t1 计算系数

给定一个多项式(by+ax)^k，请求出多项式展开后x^n*y^m 项的系数。

注意下标数字的细节

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<algorithm>
 4 using namespace std;
 5 #define ll long long
 6 #define MOD 10007
 7 #define maxk 1050
 8 ll a,b,x,y,k,n,m;
 9 ll chart[maxk][maxk];
10 inline void pre(){
11     memset(chart,0,sizeof(chart));
12     for (ll i=1;i<=k+1;i++)
13       for (ll j=1;j<=i;j++){
14           if (j==1||j==i) chart[i][j]=1;
15           else chart[i][j]=(chart[i-1][j-1]+chart[i-1][j])%MOD;
16       } 
17 }
18 int main(){
19     scanf("%lld%lld%lld%lld%lld",&a,&b,&k,&n,&m);
20     pre();
21     ll ans=chart[k+1][n+1]%MOD;
22     a%=MOD,b%=MOD;
23     for (ll i=1;i<=n;i++) ans=ans*a%MOD;
24     for (ll i=1;i<=m;i++) ans=ans*b%MOD;
25     ans%=MOD;
26     printf("%lld",ans);
27     return 0;
28 }
View Code

 

EG2 noip2017 d2t1组合数problem

题意：求对于所有的0 <= i <= n，0 <= j <= min（i，m），有多少对 (i,j)满足C（i，j）​​是k的倍数。

先预处理出n=2000内的组合数，对于符合条件的个数，维护二维前缀和

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<cmath>
 4 #include<algorithm>
 5 #define mx 2333
 6 using namespace std;
 7 int t,k;
 8 int n,m;
 9 int c[mx][mx],s[mx][mx];
10 void chart(){//节省空间，直接%k判断是否k的倍数 
11     for (int i=0;i<=2000;i++){
12         for (int j=0;j<=i;j++){
13             if (i==0&&j==0) c[i][j]=1%k;
14             else c[i][j]=(c[i-1][j-1]+c[i-1][j])%k;
15         }
16     }
17 }
18 void getsum(){//维护二维前缀和 
19     memset(s,0,sizeof(s));
20     for (int i=0;i<=2000;i++)
21       for (int j=0;j<=i;j++){
22           if ((!i)&&(!j)) s[i][j]=0;
23           else{
24               if ((!i)||i==j){
25                   s[i][j]=s[i][j-1];
26                   if (!c[i][j]) s[i][j]++;
27               }
28             else if (!j){
29                 s[i][j]=s[i-1][j];
30                 if (!c[i][j]) s[i][j]++;
31             }
32             else {
33                 s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]; 
34                 if (!c[i][j]) s[i][j]++;
35             }
36           }
37       }
38         
39 }
40 int main(){
41     scanf("%d%d",&t,&k);
42     chart();
43     getsum();
44     while (t--){
45         scanf("%d%d",&n,&m);
46         printf("%d\n",s[n][min(n,m)]);
47     }
48     return 0;
49 }
View Code

 

posted @ 2017-09-23 11:44  Vincent_hwh  阅读(428)  评论(0)  编辑  收藏  举报