高斯消元

高斯消元

设有n个未知数m个方程的线性方程组

\[\begin{cases} a_{11}x_{1}+a_{12}x_{2}+\dots+a_{1n}x{n}=b_{1} \\ a_{21}x_{1}+a_{22}x_{2}+\dots+a_{2n}x{n}=b_2 \\ \dots \dots \\ a_{m1}x_1+a_{m2}x_{2}+\dots+a_{mn}x_{n}=b_m \end{cases} \]

其中\(a_{ij}\)是第i个方程的第j个未知数的系数,\(b_i\)是第i个方程的常数项,\(i=1,2,\dots,m;j=1,2,\dots,n\)

代码实现

在化简为上三角矩阵的过程之中,通常要保证选择的主元的绝对值尽可能的大,以减小数值计算的精度误差

#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <cmath>
#include <stack>
#include <vector>
#include <map>
#include <set>
#include <array>
using namespace std;
#define x first
#define y second
#define eps 1e-6
typedef pair<int, int> PII;
typedef long long LL;
const int N = 220;
double a[N][N],x[N]; //方程左边的矩阵和等式右边的值,求解后x存的就是结果
int equ,var; // 方程数和未知数个数
int n;
//返回0表示无解1表示有解
int Gauss()
{
	// k表示当前判断是否要交换的行号,max_r是包括k当前要寻找的未知数的最大系数的行号
	int i,j,k,col,max_r;
	for(k = 0, col = 0; k < equ && col < var; k++, col++)
	{
		max_r = k;
		for(i = k + 1; i < equ; i++)
			if(fabs(a[i][col]) > fabs(a[max_r][col]))
				max_r = i; // 找到当前未知数的绝对值最大的系数的行号
		if(fabs(a[max_r][col]) < eps) return 0; // 如果系数当前要找的未知数系数等于0,则不管无穷解还是无解均返回0
		if(k != max_r)
		{
			// 将当前行换为绝对值系数最大的那一行
			for(j = col; j < var; j++) 
				swap(a[k][j],a[max_r][j]);
			swap(x[k],x[max_r]);
		}
		// 系数化为1
		x[k] /= a[k][col];
		for(j = col + 1; j < var; j++) a[k][j] /= a[k][col];
		a[k][col] = 1;
		// 将其他行的该位置未知数系数变为0
		for(i = 0; i < equ; i++)
			if(i != k)
			{
				x[i] -= x[k] * a[i][col];
				for(j = col + 1; j < var; j++) a[i][j] -=a[k][j]*a[i][col];
				a[i][col] = 0;
			}
	}
	for(int i = 0; i < n; i++) printf("%.10f\n", x[i] / a[i][i]);
	
	return 1;
}
int main()
{	
	scanf("%d",&n);
	equ = var = n;
	for(int i = 0; i < n; i++)
	{
		for(int j = 0; j < n; j++) scanf("%lf",&a[i][j]);
		scanf("%lf",&x[i]);
	}
	if(!Gauss()) printf("-1\n");

	return 0;
}

简单应用

求行列式的值

• 将矩阵A进行高斯消元,交换两行时sgn*=-1(符号)
• 最后将对角线上的值全部相乘,再乘以sgn即可

矩阵求逆

• 将矩阵A和单位矩阵E横向链接,然后进行高斯消元
• 将A编程单位矩阵时,E就变成了A的逆矩阵\(A_1\)

例题

#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <cmath>
#include <stack>
#include <vector>
#include <map>
#include <set>
#include <array>
using namespace std;
#define x first
#define y second
#define eps 1e-6
typedef pair<int, int> PII;
typedef long long LL;
const int N = 220;
double a[N][N],x[N]; //方程左边的矩阵和等式右边的值,求解后x存的就是结果
int equ,var; // 方程数和未知数个数
int n;
//返回0表示无解1表示有解
int Gauss()
{
	// k表示当前判断是否要交换的行号,max_r是包括k当前要寻找的未知数的最大系数的行号
	int i,j,k,col,max_r;
	for(k = 0, col = 0; k < equ && col < var; k++, col++)
	{
		max_r = k;
		for(i = k + 1; i < equ; i++)
			if(fabs(a[i][col]) > fabs(a[max_r][col]))
				max_r = i; // 找到当前未知数的绝对值最大的系数的行号
		if(fabs(a[max_r][col]) < eps) return 0; // 如果系数当前要找的未知数系数等于0,则不管无穷解还是无解均返回0
		if(k != max_r)
		{
			// 将当前行换为绝对值系数最大的那一行
			for(j = col; j < var; j++) 
				swap(a[k][j],a[max_r][j]);
			swap(x[k],x[max_r]);
		}
		// 系数化为1
		x[k] /= a[k][col];
		for(j = col + 1; j < var; j++) a[k][j] /= a[k][col];
		a[k][col] = 1;
		// 将其他行的该位置未知数系数变为0
		for(i = 0; i < equ; i++)
			if(i != k)
			{
				x[i] -= x[k] * a[i][col];
				for(j = col + 1; j < var; j++) a[i][j] -=a[k][j]*a[i][col];
				a[i][col] = 0;
			}
	}
	for(int i = 0; i < n; i++) printf("%.10f\n", x[i] / a[i][i]);
	
	return 1;
}
int main()
{	
	scanf("%d",&n);
	equ = var = n;
	for(int i = 0; i < n; i++)
	{
		for(int j = 0; j < n; j++) scanf("%lf",&a[i][j]);
		scanf("%lf",&x[i]);
	}
	if(!Gauss()) printf("-1\n");

	return 0;
}

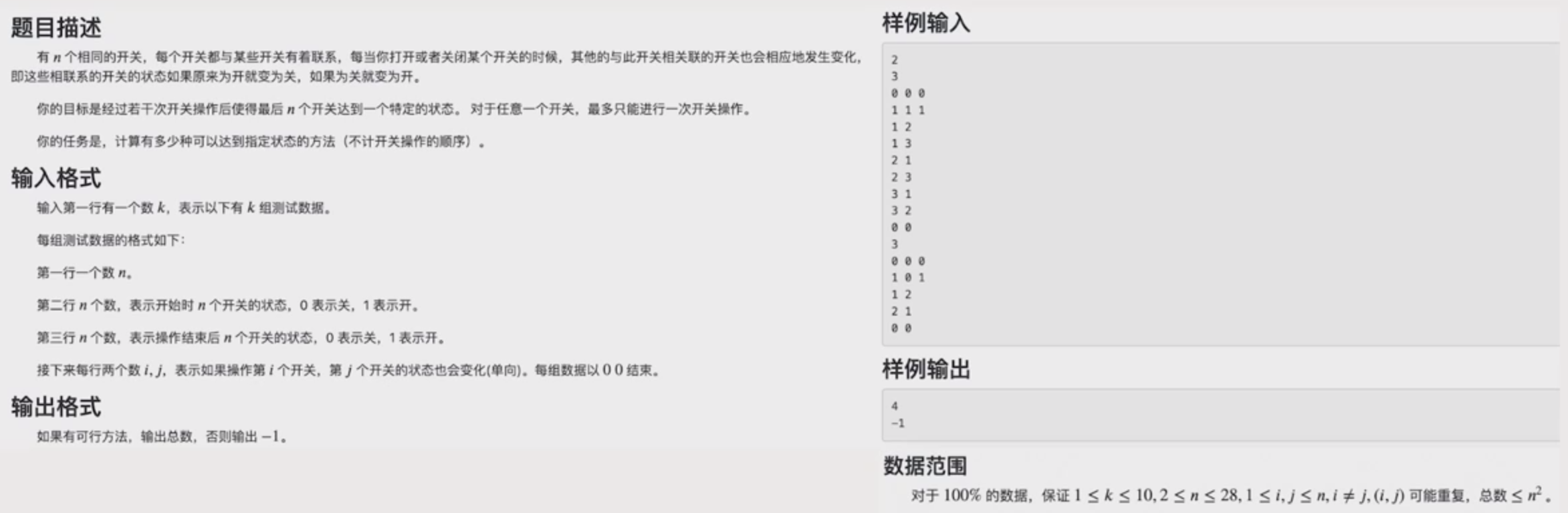
// Problem: 开关问题
// Contest: Virtual Judge - POJ
// URL: https://vjudge.net/problem/POJ-1830
// Memory Limit: 29 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <cmath>
#include <stack>
#include <vector>
#include <map>
#include <set>
#include <array>
using namespace std;
#define x first
#define y second
typedef pair<int, int> PII;
typedef long long LL;
int n,test,c[101],d[101];
int a[101][101],b[101];

void gauss()
{
	int l = 1;
	for(int i = 1; i <= n; i++)
	{
		for(int  j = l; j <= n; j++)
			if(a[j][i])
			{
				for(int k = i; k <= n; k++)
					swap(a[j][k], a[l][k]);
				swap(b[j],b[l]);
				break;
			}
		if(!a[l][i]) continue;
		for(int j = 1; j <= n; j++)
		{
			if(j != l && a[j][i])
			{
				for(int k = i; k <= n; k++)
					a[j][k] ^= a[l][k];
				b[j] ^= b[l];
			}
		}
		l++;
	}
	for(int i = l; i <= n;i++)
	{
		if(b[i])
		{
			printf("-1\n");
			return ;
		}
	}
	printf("%d\n", 1 << (n-l+1));
}

int main()
{	
	scanf("%d",&test);
	while(test--)
	{
		scanf("%d",&n);
		for(int i = 1; i <= n; i++) scanf("%d",&c[i]);
		for(int i = 1; i <= n; i++) scanf("%d",&d[i]);
		for(int i = 1; i <= n; i++) b[i] = c[i]^d[i];
		memset(a,0,sizeof(a));
		for(int i = 1; i <= n; i++) a[i][i] = 1;
		int x,y;
		while(scanf("%d%d",&x,&y),x && y)
			a[y][x] = 1;
		gauss();
	}

	return 0;
}