博弈论
简单博弈论
必胜态和必败态
假设游戏状态为有向无环图(即游戏状态可以被枚举完同时不会落入重复状态中)
- 必胜: 存在一个后继为必败态(两个状态均是先手状态,即当前局面下谁先走下一步)
- 必败: 不存在一个后继为必败态, 所有后继必胜
例:
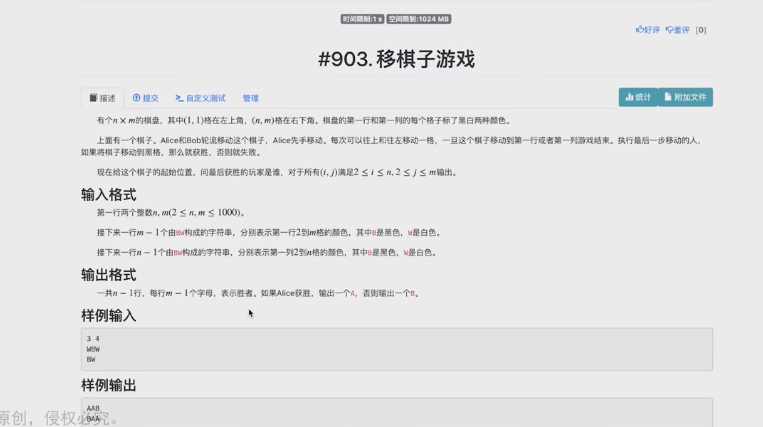
纠正条件是每次可以往上或往左移动一格
分析:
定义当前每步必胜态为1,必败态为0,枚举状态当当前状态走到下一步时有必败态是当前必胜,否则必败
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <cmath>
#include <stack>
#include <vector>
#include <map>
#include <set>
#include <array>
using namespace std;
#define x first
#define y second
typedef pair<int, int> PII;
typedef long long LL;
const int N = 2010;
int n,m,dp[N][N];
char c[N],r[N];
void output()
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cout<<dp[i][j];
}
cout<<endl;
}
}
int main()
{
scanf("%d%d",&n,&m);
scanf("%s",c+2);
scanf("%s",r+2);
for(int i = 2; i <= m; i++) dp[1][i] = (c[i] == 'W');
for(int i = 2; i <= n; i++) dp[i][1] = (r[i] == 'W');
for(int i = 2; i <= n;i++)
{
for(int j = 2; j <= m; j++)
{
if(dp[i-1][j] == 0) dp[i][j] = 1;
if(dp[i][j-1] == 0) dp[i][j] = 1;
if(dp[i][j]) printf("A");
else printf("B");
}
puts("");
}
// output();
return 0;
}

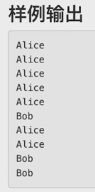
平等博弈两者状态相同,同一局面对于两个人的必胜必败状态相同
不平等则可能导致同一局面对两个人的状态一个必胜一个必败
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <cmath>
#include <stack>
#include <vector>
#include <map>
#include <set>
#include <array>
using namespace std;
#define x first
#define y second
typedef pair<int, int> PII;
typedef long long LL;
const int N = 2e3+10;
int n1,n2,m;
int a[N],b[N];
int dp1[N],dp2[N];
int main()
{
scanf("%d%d%d",&n1,&n2,&m);
for(int i = 1; i <= n1; i++) scanf("%d",&a[i]);
for(int i = 1; i <= n2; i++) scanf("%d",&b[i]);
for(int i = 1; i <= m; i++)
{
for(int j = 1; j <= n1; j++)
{
if(i >= a[j] && !dp2[i-a[j]])
{
dp1[i] = 1;
break;
}
}
for(int j = 1; j <= n2; j++)
{
if(i >= b[j] && !dp1[i-b[j]])
{
dp2[i] = 1;
break;
}
}
puts(dp1[i] ? "Alice" : "Bob");
}
return 0;
}
经典模型
巴什博弈
n个石子,两个人轮流取每个人取1~m个谁能赢
- 结论: \((m+1)|n\)为必败态否则必胜态
威佐夫博弈
两堆石子(a,b)
- 选一堆 -x
- 两堆都 -x
模板
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <cmath>
#include <stack>
#include <vector>
#include <map>
#include <set>
#include <array>
using namespace std;
#define x first
#define y second
typedef pair<int, int> PII;
typedef long long LL;
const int N = 2e3 + 10;
int dp[N][N];
int main()
{
int M = 100;
for(int i = 0; i <= M; i++)
{
for(int j = 0; j <= M; j++)
{
for(int x = 1; x <= i; x++)
if(dp[i - x][j] == 0) dp[i][j] = 1;
for(int x = 1; x <= j; x++)
if(dp[i][j - x] == 0) dp[i][j] = 1;
for(int x = 1; x <= i && x <= j; x++)
if(dp[i - x][j - x] == 0 ) dp[i][j] = 1;
if(dp[i][j] == 0) printf("%d %d\n", i, j);
}
}
return 0;
}
NIM博弈
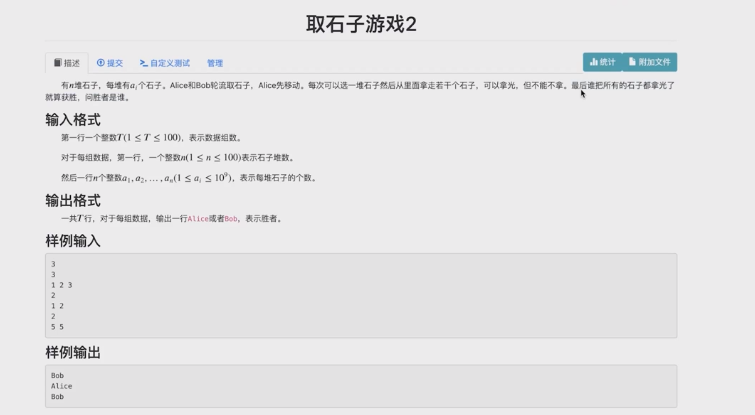
结论: \(A_{1} \bigoplus A_{2} \bigoplus \dots \bigoplus A_{n} = 0\)时必败态,否则必胜
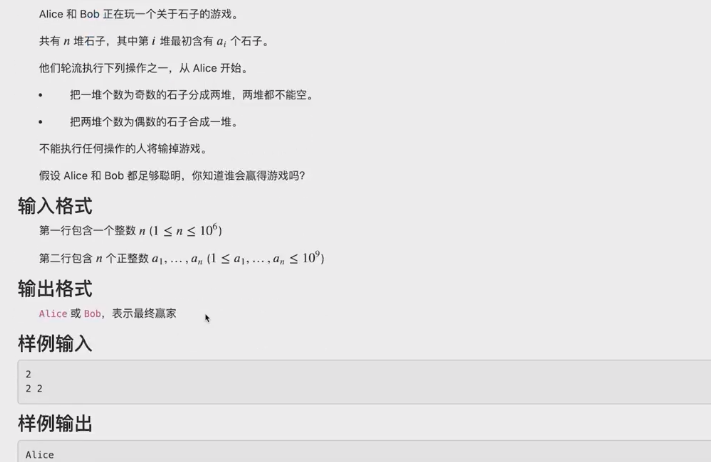
分析: 结束情况,所有奇数为1,且只剩下一个偶数
每个人操作完后堆数要么加一要么减一, 同时起始状态的奇偶性和最终状态奇偶性我们知道,看在谁中的堆数的奇偶性即可
怎么得知最终状态堆数的奇偶性呢?
\(odd\rightarrow odd +even\)
\(even + even\rightarrow even\)
最后所有的偶数堆被合并为只有一个,而奇数堆数目不变,且当奇数堆不全为1时,最终状态的堆数一定比当前奇数堆个数大一
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <cmath>
#include <stack>
#include <vector>
#include <map>
#include <set>
#include <array>
using namespace std;
#define x first
#define y second
typedef pair<int, int> PII;
typedef long long LL;
int main()
{
int n; scanf("%d",&n);
int odd = 0, one = 0;
for(int i = 0; i < n;i++)
{
int x; scanf("%d",&x);
if(x % 2 == 1) odd++;
if(x == 1) one++;
}
if(one != n) odd++;
if((odd % 2) == (n % 2)) puts("Bob");
else puts("Alice");
return 0;
}
\[必败:\space>\frac{n}{2} = 0 \leftarrow 必胜: 1 \sim \frac{n}{2} = 1 \leftarrow 必败: > \frac{n}{2} = 1 \leftarrow 必胜: 1 \sim \frac{n}{2} =1 \dots 必败: >\frac{n}{2} = min(a_{i}) \leftarrow 必胜: 1 \sim \frac{n}{2} = min(a_{i})
\]
逆推公式如上,先从必败入手条件很明了,然后由必败推出上一步必胜态,此后类似套娃,直至我们会推出条件是\(a_i\)最小的必败态此时就是题目上的条件并无法再次推广
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <cmath>
#include <stack>
#include <vector>
#include <map>
#include <set>
#include <array>
using namespace std;
#define x first
#define y second
typedef pair<int, int> PII;
typedef long long LL;
const int N = 2e6+10;
int n;
int a[N];
int main()
{
scanf("%d",&n);
int mn = 1e9+10, cnt = 0;
for(int i = 0; i < n; i++)
{
int x; scanf("%d",&x);
if(x < mn) mn = x, cnt = 0;
else if(x == mn) cnt++;
}
if(cnt >= (n >> 1)) puts("Bob");
else puts("Alice");
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号