动态规划(DP)概述

- 搜索,dfs依次枚举每一步向上走多少台阶,最后统计有多少可行的方案。(小规模可以,大规模gg)
- 组合数学

- 递归
考虑最后一步,我们只能从第9级或者第8级走过去。
对于任意的\(n\geq 2\)时有\(f(n) = f(n-2) + f(n - 1)\)
如果不递归
| 台阶数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 走法数 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 |
可以从小到大,一个一个计算出所有的f(i)! 这就是简单的动态规划
dp两个要求:
- 最优子结构:大问题的(最优)解可以由小问题(最优)解推出,在这个问题中,大问题\(f(n)\)解可以由小问题\(f(n-2)和f(n-1)\)
的解推出。注意问题拆解g过程中不能无限递归 - 无后效性:未来与过去无关,一旦得到了一个小问题的解,如何得到它的解的过程不影响大问题的求解。在这个题中,要求出f(n),只需要知道f(n- 1)和f(n- 2)的值,而它们到底是怎么得到的已经不关键了。
dp两个元素
- 状态:求解过程进行到了哪一步,可以理解为一个子问题;
- 转移:从一个状态(小问题)的(最优)解推导出另一个状态(大问题)的(最优)解的过程
例题
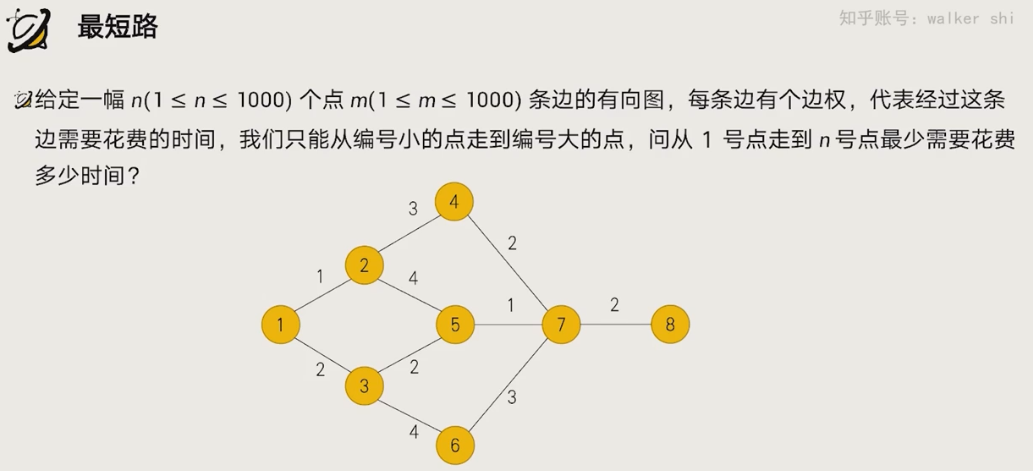
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <cmath>
#include <stack>
#include <vector>
#include <map>
#include <set>
#include <array>
using namespace std;
#define x first
#define y second
typedef pair<int, int> PII;
typedef long long LL;
const int N = 1e3+10;
int n, m;
int a[N][N], f[N];
int main()
{
scanf("%d%d", &n, &m);
memset(a, 0x3f, sizeof(a));
for(int i = 1; i <= m; i++){
int x, y, z; scanf("%d%d%d",&x,&y,&z);
a[x][y] = min(a[x][y], z);
}
memset(f, 0x3f, sizeof(f));
f[1] = 0;
for(int i = 2; i <= n; i++){
for(int j = 1; j <= i; j++){
if(f[j] < 1 << 30 && a[j][i] < 1<<30) f[i] = min(f[i],f[j]+a[j][i]);
}
}
printf("%d\n",f[n]);
return 0;
}
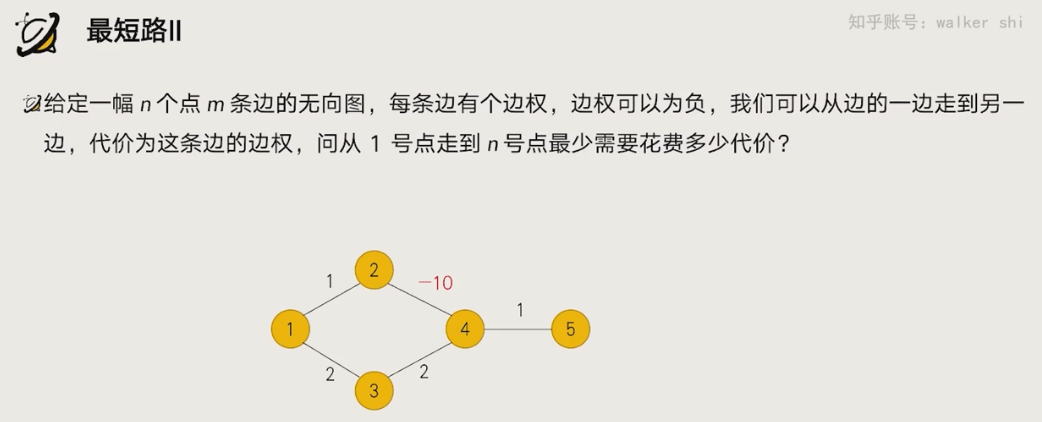
最优子结构:问题拆解过程中不能无限递归,但在这里会有一个环路每经过一圈就会减小,无限递归

#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int n;
int a[N],f[N];
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n;i++){
f[i]=1;
for(int j=1;j<i;j++){
if(a[j]<a[i]){
f[i]=max(f[j]+1,f[i]);
}
}
}
int ans=0;
for(int i=1;i<=n;i++) ans=max(ans,f[i]);
cout<<ans;
return 0;
}

#include<bits/stdc++.h>
using namespace std;
int n,m;
string a,b;
int f[1010][1010];
int main(){
cin>>n>>m;
cin>>a>>b;
a=" "+a;
b=" "+b;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
f[i][j]=max(f[i-1][j],f[i][j-1]);
if(a[i]==b[j]) f[i][j]=max(f[i][j],f[i-1][j-1]+1);
}
}
cout<<f[n][m];
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号