14.python数 二叉树、满二叉树、完全二叉树、二叉树遍历、广度优先遍历：层序遍历、深度优先遍历：前序、中序、后序遍历

树

定义：树是非线性结构，是n个（n≥0）元素的集合。
n为0时，称为空树。
树中只有一个特殊的没有前驱的元素，称为树的根 Root。
树中除了除了根结点外，其余元素只能有一个前驱，可以有零个或多个后继。

递归定义：树T是n(n≥0)个元素的集合。n=0时，称为空树。
有且只有一个特殊元素根，剩余元素都可以被划分为m个互不相交的集合T1、T2、T3、...、Tm，而每一个集合都是树，称为T的子树Subtree。
子树也有自己的根。

名词解释

• 结点(Vertex)：树中的数据元素
• 结点的度degree：结点拥有的子树的数目称为度，记作d(v)
• 叶子结点：结点的度为0，称为叶子结点leaf、终端结点、末端结点
• 分支结点：结点的度不为0，称为非终端结点或分支结点
• 分支：结点之间的关系
• 内部结点：除根结点外的分支结点，当然也不包括叶子结点
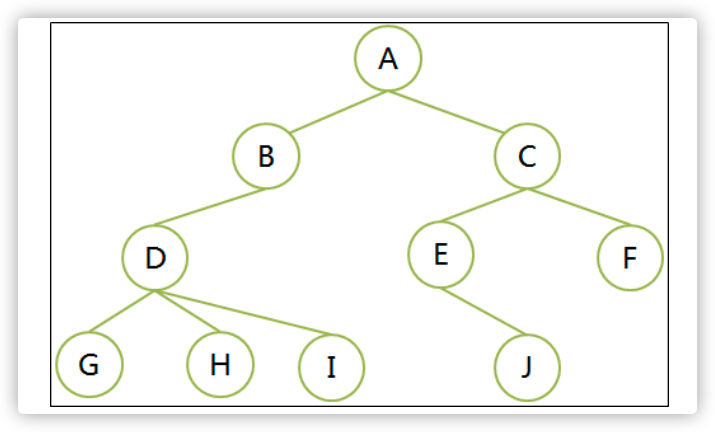
• 树的度是树内各结点的度的最大值。D结点度最大为3，树的度数就是3

• 孩子（儿子Child）结点：结点的子树的根结点成为该结点的孩子

• 双亲（父Parent）结点：一个结点是它各子树的根结点的双亲

• 兄弟（Sibling）结点：具有相同双亲结点的结点

• 祖先结点：从根结点到该结点所经分支上所有的结点。A、B、D都是G的祖先结点

• 子孙结点：结点的所有子树上的结点都称为该结点的子孙。B的子孙是D、G、H、I

• 结点的层次（Level）：根节点为第一层，根的孩子为第二层，以此类推，记作L(v)

• 树的深度（高度Depth）：树的层次的最大值。上图的树深度为4

• 堂兄弟：双亲在同一层的结点

• 有序树：结点的子树是有顺序的（兄弟有大小，有先后次序），不能交换。

• 无序树：结点的子树是有无序的，可以交换。

• 路径：树中的k个结点n1、n2、...、nk，满足ni是n(i+1)的双亲，称为n1到nk的一条路径。就是一条线串下来的，前一个都是后一个的父（前驱）结点。

• 路径长度=路径上结点数-1，也是分支数

• 森林：m(m≥0)棵不相交的树的集合

  • 对于结点而言，其子树的集合就是森林。A结点的2棵子树的集合就是森林

特点

• 唯一的根
• 子树不相交
• 除了根以外，每个元素只能有一个前驱，可以有零个或多个后继
• 根结点没有双亲结点（前驱），叶子结点没有孩子结点（后继）
• vi是vj的双亲，则L(vi) = L(vj)-1，也就是说双亲比孩子结点的层次小1

思考：堂兄弟的双亲是兄弟关系吗？

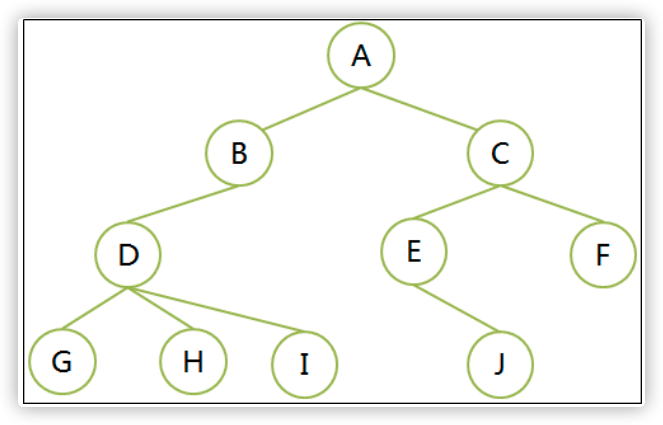
堂兄弟定义是，双亲结点是同一层的节点。右图G和J是堂兄弟，因为它们的双亲结点D和E在第三层，依然是堂兄弟。因此，堂兄弟的双亲不一定是兄弟关系。

二叉树

概念

• 每个结点最多2棵子树
• 二叉树不存在度数大于2的结点
• 它是有序树，左子树、右子树是顺序的，不能交换次序
• 即使某个结点只有一棵子树，也要确定它是左子树还是右子树

二叉树的五种基本形态

• 空二叉树
• 只有一个根结点
• 根结点只有左子树
• 根结点只有右子树
• 根结点有左子树和右子树

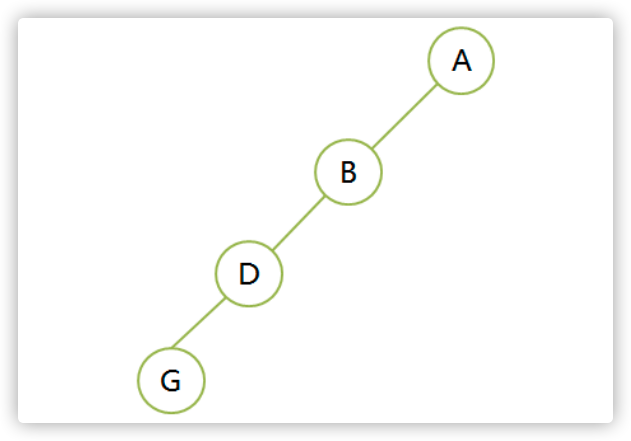
斜树

左斜树，所有结点都只有左子树；右斜树，所有节点都只有右子树

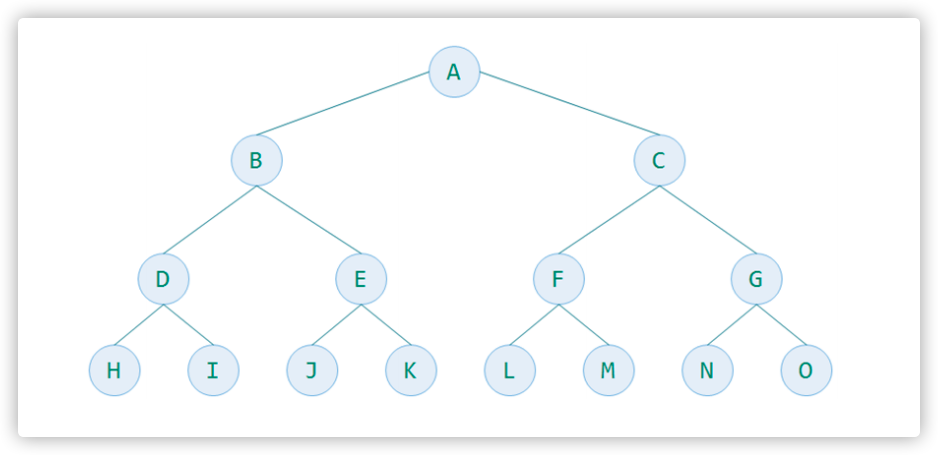
满二叉树

• 一棵二叉树的所有分支结点都存在左子树和右子树，并且所有叶子结点只存在在最下面一层
• 同样深度二叉树中，满二叉树结点最多
• k为深度（1≤k≤n），则结点总数为2^k-1
• 如下图，一个深度为4的15个结点的满二叉树

完全二叉树

完全二叉树Complete Binary Tree

• 若二叉树的深度为k，二叉树的层数从1到k-1层的结点数都达到了最大个数，在第k层的所有结点都集中在最左边，这就是完全二叉树
• 完全二叉树由满二叉树引出
• 满二叉树一定是完全二叉树，但完全二叉树不一定是满二叉树
• k为深度（1≤k≤n），则结点总数最大值为2^k-1，当达到最大值的时候就是满二叉树

下图三个数都是完全二叉树，最下一层的叶子结点都连续的集中在左边

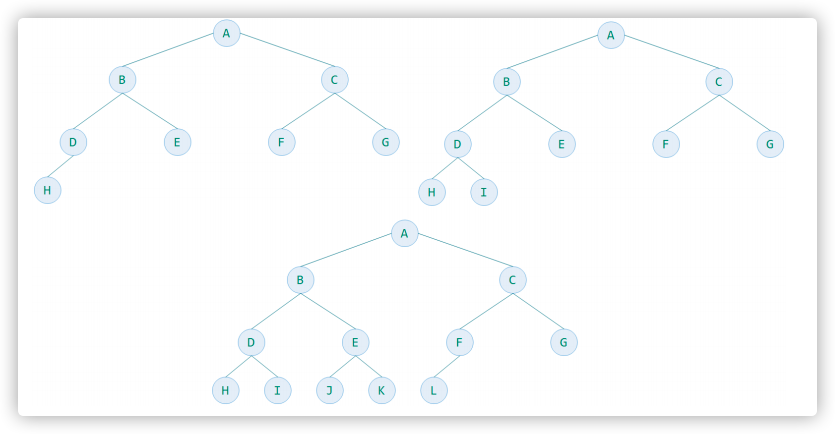
下面2个树是完全二叉树吗？

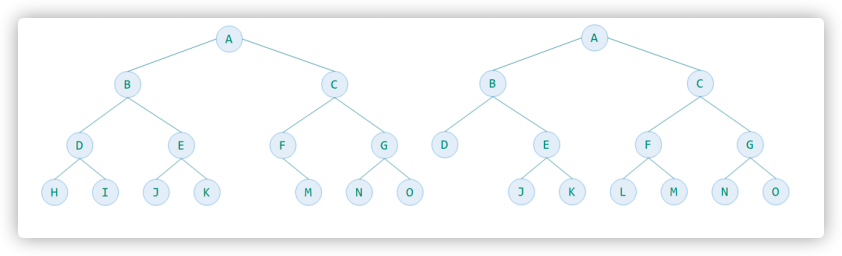
上图的树都不是完全二叉树，它们叶子节点都没有集中到左边。

性质

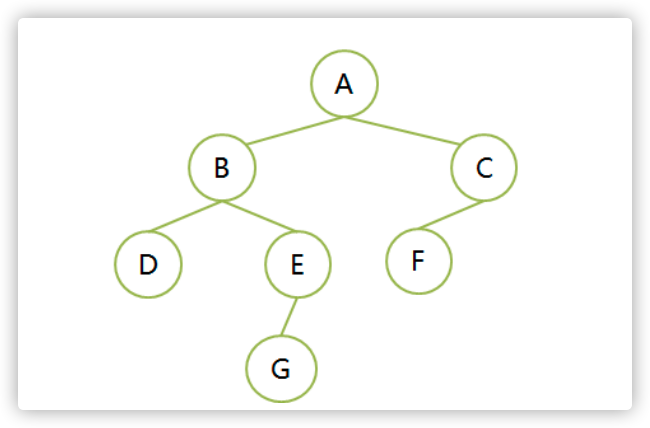
• 性质1：在二叉树的第i层上至多有2^(i-1)个结点(i≥1)
• 性质2：深度为k的二叉树，至多有2^k-1个节点(k≥1)
  • 一层 2-1=1
  • 二层 4-1=1+2=3
  • 三层 8-1=1+2+4=7
• 性质3：对任何一棵二叉树T，如果其终端节点数为n0，度数为2的结点为n2，则有n0=n2+1
  • 换句话说，就是叶子结点数-1就等于度数为2的结点数
  • 证明
    • 总结点数为n=n0+n1+n2，n1为度数为1的结点总数
    • 一棵树的分支数为n-1，因为除了根结点外，其余结点都有一个分支，即n0+n1+n2-1
    • 分支数还等于 n00+n11+n22 ，n2是2分支结点所以乘以2，2n2+n1
    • 可得2*n2+n1=n0+n1+n2-1 => n2=n0-1

其他性质

• 高度为k的二叉树，至少有k个结点
• 含有n（n≥1）的结点的二叉树高度至多为n。和上句一个意思
• 含有n（n≥1）的结点的二叉树的高度至多为n，最小为math.ceil(log2 (n+1))，不小于对数值的最小整数，向上取整
  • 假设高度为h，2^h-1=n => h = log2 (n+1)，层次数是取整。如果是8个节点，3.1699就要向上取整为4，为4层
• 性质4：具有n个结点的完全二叉树的深度为int(log2n)+1或者math.ceil(log2(n+1))

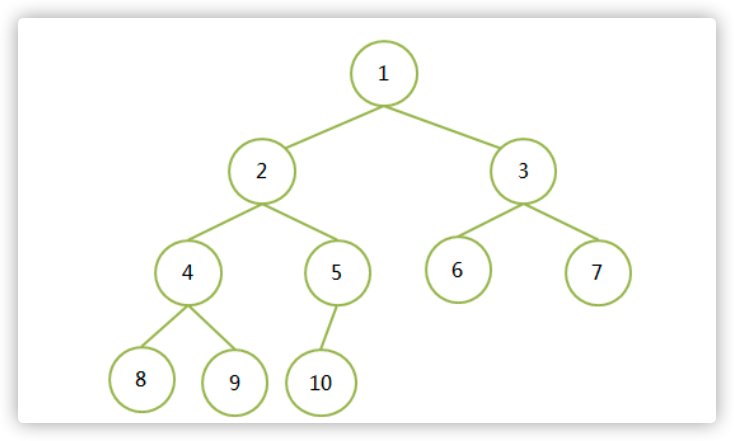
• 性质5:
  • 如果有一棵n个结点的完全二叉树（深度为性质4），结点按照层序编号，如上图
  • 如果i=1，则结点i是二叉树的根，无双亲；如果i>1，则其双亲是int(i/2)，向下取整。就是子节点的编号整除2得到的就是父结点的编号。父结点如果是i，那么左孩子结点就是2i，右孩子结点就是2i+1
  • 如果2i>n，则结点i无左孩子，即结点i为叶子结点；否则其左孩子结点存在编号为2i
  • 如果2i+1>n，则结点i无右孩子，注意这里并不能说明结点i没有左孩子；否则右孩子结点存在编号为2i+1

二叉树的遍历

遍历：迭代所有元素一遍
树的遍历：对树中所有元素不重复地访问一遍，也称作扫描。

• 广度优先遍历
  • 层序遍历
• 深度优先遍历
  • 前序遍历
  • 中序遍历
  • 后序遍历
• 遍历序列：将树中所有元素遍历一遍后，得到的元素的序列。将层次结构转换成了线性结构

广度优先遍历

层序遍历

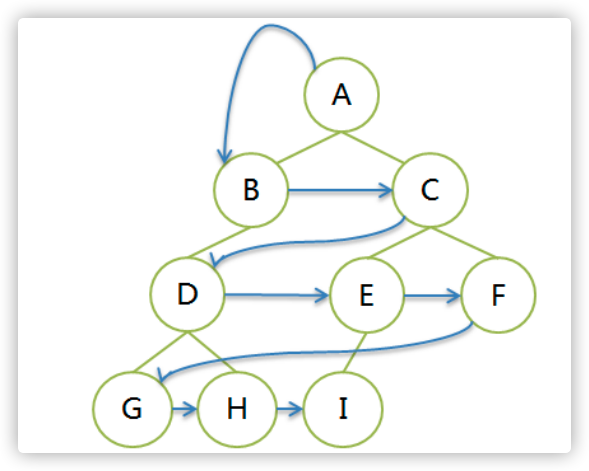
层序遍历是广度优先遍历。按照树的层次，从第一层开始，自左向右遍历元素。
遍历序列：ABCDEFGHI

深度优先遍历

设树的根结点为D，左子树为L，右子树为R，且要求L一定在R之前，则有下面几种遍历方式

1. 前序遍历，也叫先序遍历、也叫先根遍历，DLR
2. 中序遍历，也叫中根遍历，LDR
3. 后序遍历，也叫后根遍历，LRD

前序遍历DLR

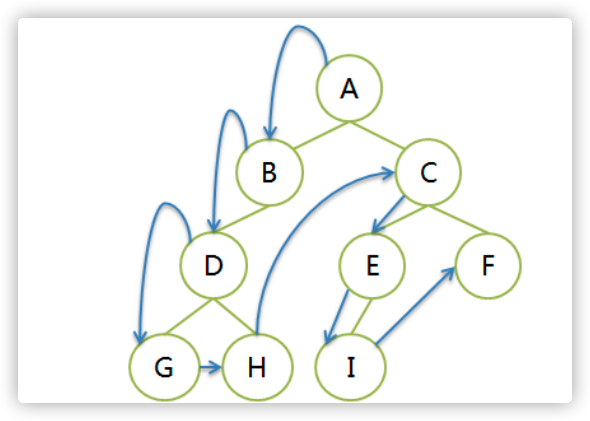
从根结点开始，先左子树后右子树。每个子树内部依然是先根结点，再左子树后右子树。递归遍历。
遍历序列：A BDGH CEIF

中序遍历LDR

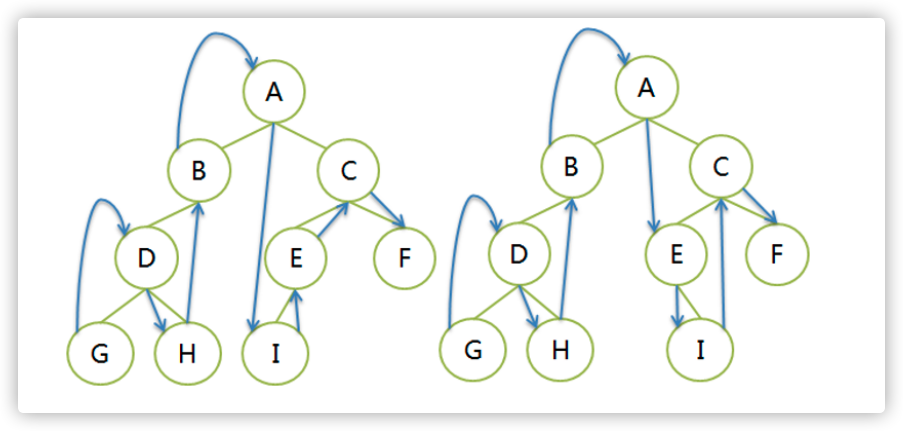
从根结点的左子树开始遍历，然后是根结点，再右子树。每个子树内部，也是先左子树，后根结点，再右子树。递归遍历。
左图遍历序列：GDHB A IECF
右图遍历序列：GDHB A EICF

后序遍历LRD

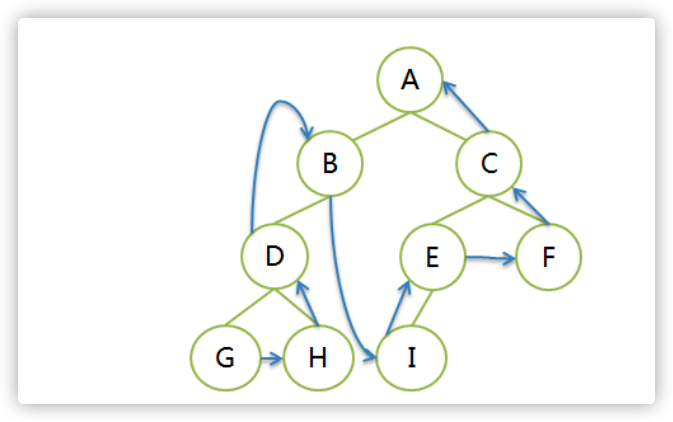
先左子树，后右子树，再根结点。每个子树内部依然是先左子树，后右子树，再根结点。递归遍历。
遍历序列：GHDB IEFC A