机器数与码制——如何在计算机内部存储数字、进行数据运算

机器数

机器数

　　各种数据在计算机内部的表示和存储形式称为机器数。

　　特点：

• 采用二进制计数；
• 数的符号（正负）用“0、1”表示；
• 小数点隐含表示二不占位置。

机器数的真值

　　机器数所对应的实际数值。　

机器数的分类

　　无符号机器数和带符号机器数。　

无符号机器数（表示正数）

　　无符号(无正负号)机器数表示正数，全部二进制位均代表数值，没有符号位。

• 若约定小数点的位置在机器数的最低位之后，则是纯整数(正整数)。
• 若约定小数点的位置在机器数的最高位之前，则是纯小数(正小数)。
• 不能用原码、反码、补码等编码方法表示。

带符号机器数(表示实数)

　　带符号机器数既可以表示正数，也可以表示负数。

　　最高位是符号位("0"表示“+”。“1”表示“-”)，其余位表示数值。

• 若约定小数点的位置在机器数的最低位之后，则是纯整数。
• 若约定小数点的位置在机器数的最高位之前，则是纯小数。
• 可采用原码、反码、补码等编码方法表示。

码制

　　为了运算方便，带符号的机器数可采用原码、反码、补码、移码等不同的编码方式表示。

　　这些编码方法被称为码制。

原码表示

规则：

• 数值X的原码记为[X]_原；
• 机器字长为n,即采用n个二进制位表示数据。
• 最高位为符号位，“0”表示正号，“1”表示负号。
• 其余的n-1位表示数值的绝对值。
• 对数“0”有“+0”和“- 0”两种表示形式。
• 对于机器字长为n+1位的机器，原码表示法可表示的整型数值范围为：-2ⁿ+1 ≤ X ≤ 2ⁿ-1。
• 当X ≥ 0时，[X]_原 = 0X；　　eg：[+7]_原 = 00000111 (设机器字长为8)。
• 当X ≤ 0时，[X]_原 = 1X；　　eg：[- 7]_原 = 10000111 (设机器字长为8)。
• [+0]_原 = 00000000；
• [- 0]_原 = 10000000；

Example-1：

　　　　[+1]_原 = 00000001；　　[-1]_原 = 10000001。

　　　　[+127]_原 = 01111111；　　[-127]_原 = 11111111。注：(127)_D = (1111111)_B。

　　　　[+45]_原 = 00101101；　　[-45]_原 = 10101101。 注：(45)_D = (101101)_B。

反码表示

规则：

• 数值X的反码记为[X]_反；
• 机器字长为n,即采用n个二进制位表示数据。
• 最高位为符号位，“0”表示正号，“1”表示负号。
• 其余的n-1位表示数值。
• 对数“0”有“+0”和“-0”两种表示形式。
• 对于机器字长为n+1位的机器，反码表示法可表示的整型数值范围为：-2ⁿ+1 ≤ X ≤ 2ⁿ-1。
• 正数的反码与原码相同。即当X ≥ 0时，[X]_反 = [X]_原 = 0X。
• 负数的反码则是要将除符号位外的绝对值按位取反。
• 当X ≥ 0时，[X]_反 = 0 X；　　eg：[+7]_反 [+7]_原 = 00000111 (设机器字长为8)。
• 当X ≤ 0时，[X]_反 = 1 |X|；　　eg：[- 7]_反 = 11111000 (设机器字长为8)。
• [+0]_反 = 00000000；
• [- 0]_反 = 11111111；

Example-1：

　　　　[+1]_反 = 00000001；　　[-1]_反 = 11111110。

　　　　[+127]_反 = 01111111；　　[-127]_反 = 10000000。注：(127)_D = (1111111)_B。

　　　　[+45]_反 = 00101101；　　[-45]_反 = 11010010。 注：(45)_D = (101101)_B。

补码表示

规则：

• 数值X的补码记为[X]_补；
• 机器字长为n,即采用n个二进制位表示数据。
• 最高位为符号位，“0”表示正号，“1”表示负号。
• 其余的n-1位表示数值。
• 对数“0”只有唯一的“0”一种表示形式。
• [+0]_补 = 00000000；
• [- 0]_补 = 00000000；
• 对于机器字长为n+1位的机器，反码表示法可表示的整型数值范围为：-2ⁿ ≤ X ≤ 2ⁿ-1。
• 正数的补码与其反码和原码相同。即当X ≥ 0时，[X]_补 = [X]_反 = [X]_原 = 0X。
• 负数的补码则等于在其反码的末尾加1(将其原码除符号位外的其他位按位取反后加1)。
• 当X ≥ 0时，[X]_补 = [X]_反 = [X]_原 = 0X；　　eg：[+7]_补 = [+7]_反 = [+7]_原 = 00000111 (设机器字长为8)。
• 当X < 0时，[X]_补 = 1 |X| +1　　eg：[- 7]_补 = 11111001  [- 7]反 =  11111000(设机器字长为8)。

Example-1：

　　　　[+1]_补 = 00000001；　　[- 1]_反 = 11111110；　　[- 1]_补 = 11111111。

　　　　[+127]_补 = 01111111；　　[- 127]_反 = 10000000；　　[- 127]_补 = 10000001。注：(127)_D = (1111111)_B。

　　　　[+45]_补 = 00101101；　　[- 45]_反 = 11010010；　　[- 45]_补 = 11010011。 注：(45)_D = (101101)_B。

补码运算的优点(功能)

　　将减法运算变成加法运算(因为运算器中只有加法器)。

　　例如计算96 - 20 = ？。

	96	-20	76
无符号位二进制表示	1100000	-10100	1001100
原码	01100000	10010100	01001100
反码	01100000	11101011	01001100
补码	01100000	11101100	01001100

　　将96-20转换为[96]_补 + [-20]_补，计算过程如下：

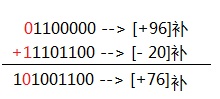
　　最高位的进位1自然丢失。

补码表示的一个另外情况(原码、反码表示无此情况)

　　对于n位补码表示法，当符号位为1而数值位全部为0时，它表示整数 -2^n-1,即此时符号位的1，既表示负数又表示数值。

　　Eg:当机器字长为8时，符号位为1而数值位全部为0为数值 10000000，(10000000)_B = (128)_D = 2^8-1 = 2⁷ = 128。且符号位还表示负号。

　　所以[- 128]补 = 10000000。

补码的另一特点

　　用补码表示时，由于符号位和数值位一起编码，难以从补码码值形式判断真值大小。如45 > - 45，然而，[45]_补 = 00101101 < [- 45]_补 = 11010011。

移码(增码)表示

　　移码（又叫增码）是符号位取反的补码，将补码的符号位取反即可得到移码表示；一般用做浮点数的阶码，引入的目的是为了保证浮点数的机器零为全0。

　　采用移码表示时，码值与真值大小成正比，码值大者对应的真值也大。

规则：

• 最高位为符号位，“1”表示正号，“0”表示负号。
• 机器字长为n,即采用n个二进制位表示数据。
• 当-2ⁿ ≤ X ≤ 2ⁿ时，[X]_移 = 2ⁿ+X。

特点：

• 保持了数据原有的大小顺序，便于进行比较操作。

机器数的运算

机器数的加减运算

　　在计算机中，可以只设置加法器，而将减法运算转换为加法运算来实现。

原码加、减法

•  两个符号相同的原码数相加时，只需将数值部分直接相加，运算结果的符号与两个加数的符号相同。
• 若两个加数的符号相异，则应进行减法运算。方法：先比较两个数绝对值的大小，然后用绝对值大者的绝对值减去绝对值小者的绝对值，结果的符号取绝对值大者的符号。

　　原码表示的机器数进行减法运算是很烦的，所以在计算机中的加、减法运算主要采用补码表示的机器数。

补码加、减法

 　　计算机中的加、减法运算一般用补码来实现。

　　在补码表示中，可将减法运算转换成加法运算。

补码加法：

　　和的补码等于补码求和。　　[X+Y]_补 = [X]_补+[Y]_补

补码减法：

　　差的补码等于被减数的补码加上减数取负后的补码。　　[X-Y]_补 = [X]_补+[-Y]_补

• 由[X]_补求[-X]_补的方法：
• 将[X]_补的各位取反(包括符号位)，末尾加1。

总结：

　　X±Y → [X+Y]_补=[X]_补+[±Y]_补

　　Example-1:

　　　　设二进制整数X = +1000100, Y = +1110,求X+Y与X-Y的值。

　　　　解：

　　　　　　　　设用8位补码表示带符号机器数

　　　　　　　　因为X和Y都是正数

　　　　　　　　所以[X]_补 = 01000100，[Y]_补 = 00001110；

　　　　　　　　

溢出及其判定

 

机器数的乘除运算

　　机器数的乘除法运算，通常有如下3种实现形式：

　　　　1.纯软件方案。在只有加法器的低档计算机中，没有乘、除法指令，乘除运算使用程序来实现的。这种方案的硬件结构简单，但作乘除法运算时速度缓慢。

　　　　2.在现有的能够完成加减运算的算术逻辑单元ALU的基础上，通过增加少量的左、右移位的逻辑电路，来实现乘除运算。与纯软件方案相比，这种方案增加硬件不多，而乘除法的运算速度有了较大提高。

　　　　3.设置专用的硬件阵列乘法器(或除法器)，完成乘除法运算。该方案需付出较高的硬件代价，可获得最高的执行速度。